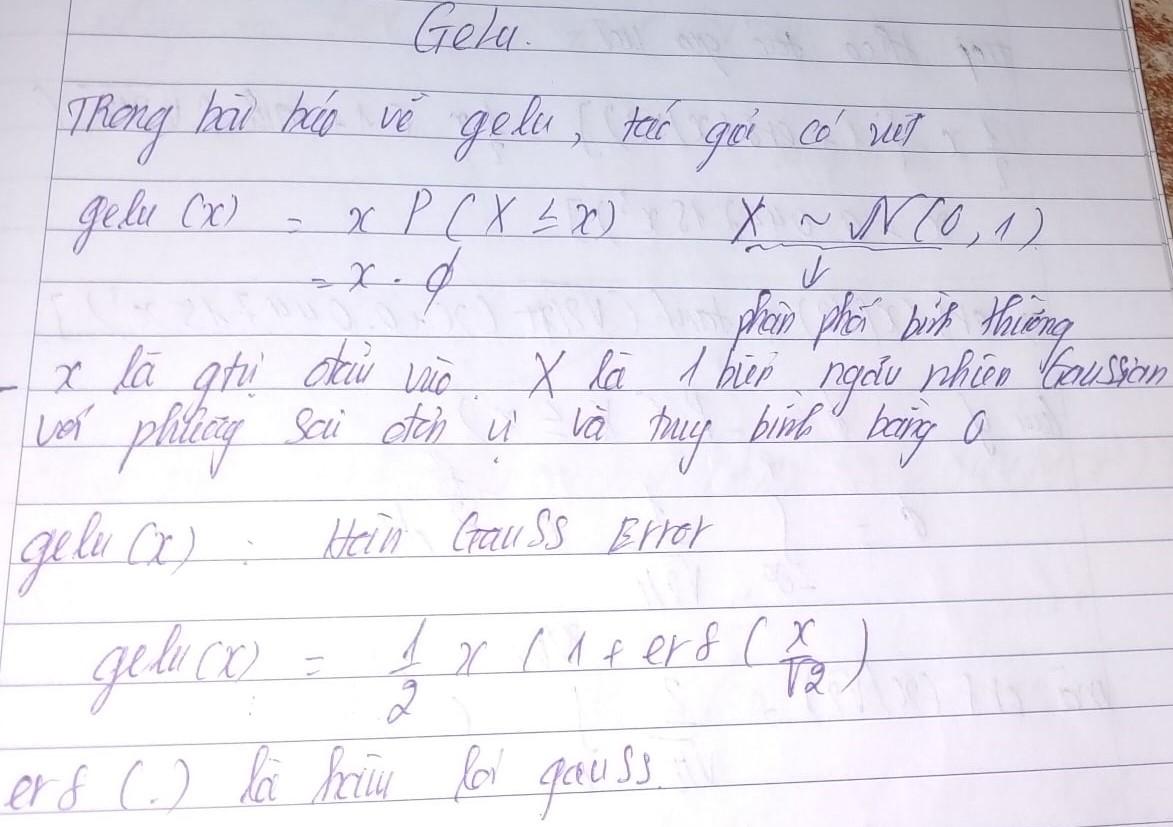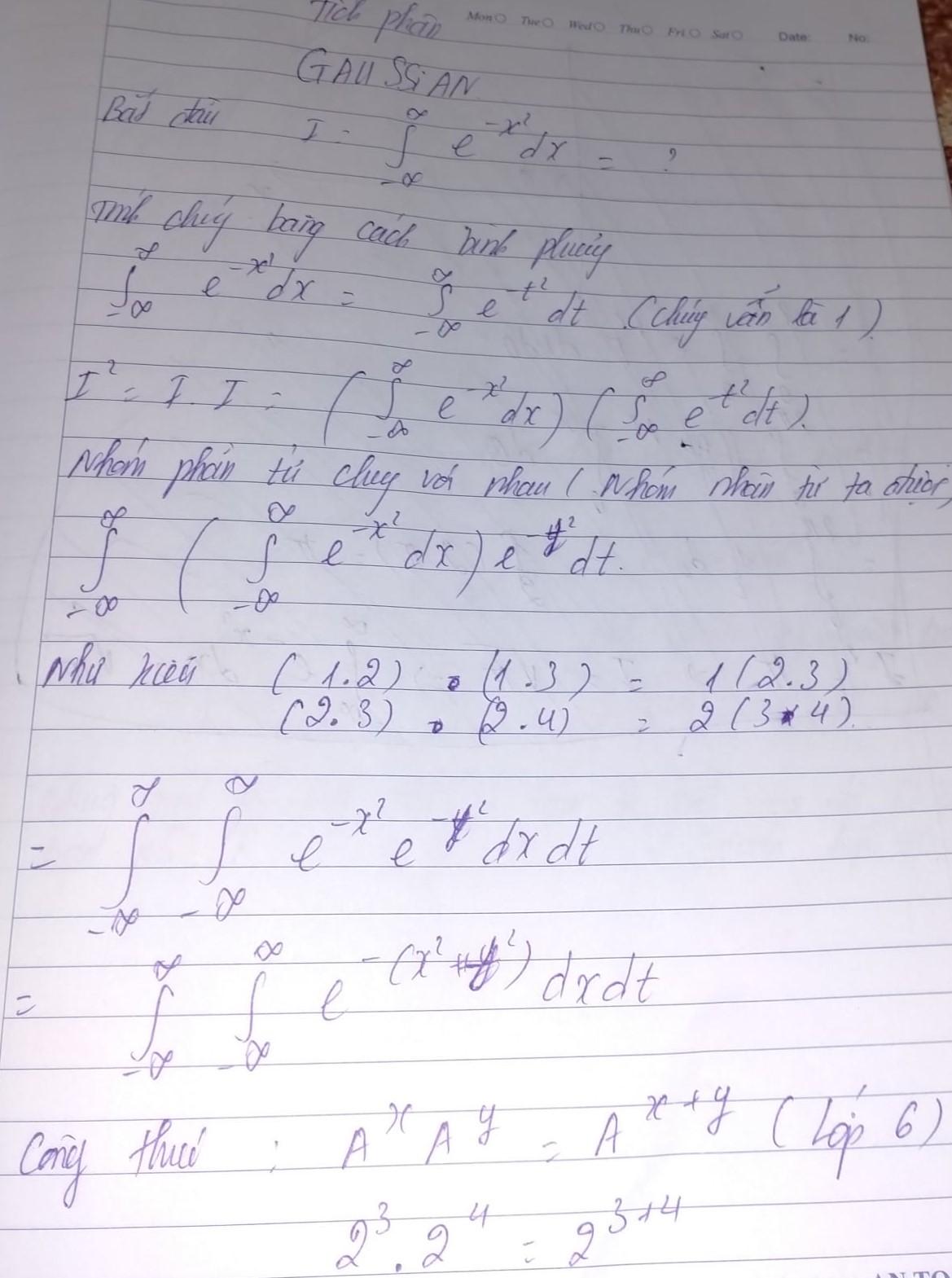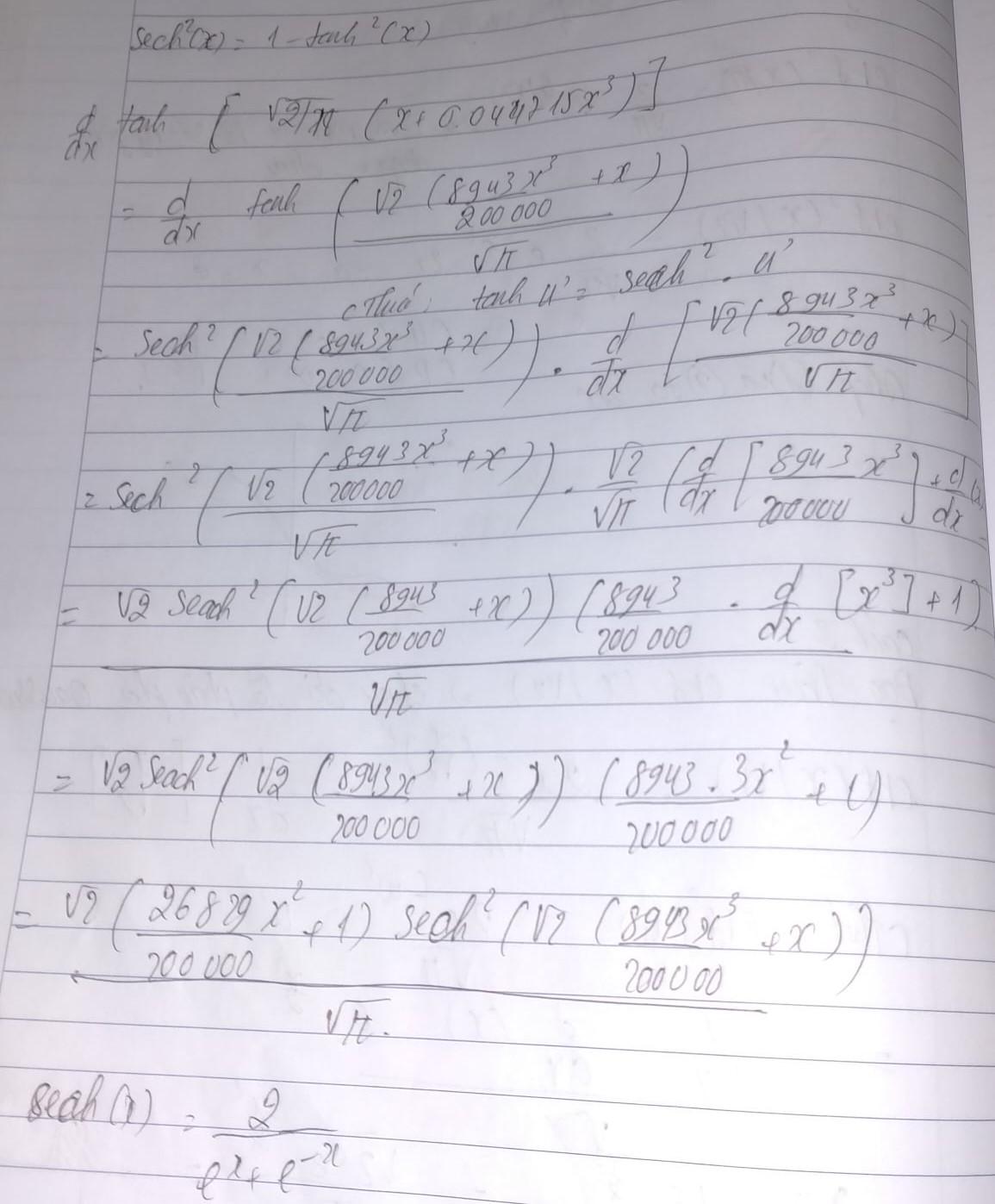Khám phá activation function Gelu(Transformers)

Phần 1 . Lời nói đầu

Trong bài viết này chúng ta sẽ bắt đầu tìm hiểu một số chi tiết chưa có trong bài báo https://arxiv.org/abs/1606.08415v4 (Gaussian Error Linear Units). Hay cò gọi là activation function Gelu , chúng ta biết được rằng transformer hiện nay được sử dụng rộng rãi thông qua các activation function gelu thay vì sử dụng các activation function tanh, sigmoid như lúc trước.

Bài báo được trình bày bởi 2 tác giả Dan Hendrycks (University of California, Berkeley) và Kevin Gimpel (Toyota Technological Institute at Chicago) . Trong bài báo tác giả có nói chúng tôi sử dụng activation function gelu từ sự kết hợp đầu vào $x$ và phân phối gaussian tiêu chuẩn . Đặc điểm để các activation gelu tốt hơn các activation function như ngày này là nguyên nhân nằm ở chính phân phôi chuẩn (standard normal distribution). Hãy cùng đón xem tại sao tác giả lại coi chúng có tác dụng hơn các activation function khác.

Hàm sigmoid là một hàm kích hoạt phổ biến được sử dụng trong các mạng thần kinh. Nó ánh xạ bất kỳ giá trị đầu vào nào thành một giá trị trong khoảng từ 0 đến 1. Khi đầu vào của hàm sigmoid rất lớn hoặc rất nhỏ, đầu ra của hàm sigmoid có xu hướng bão hòa về phía giới hạn trên hoặc dưới của hàm, dẫn đến gradient gần bằng không.

Khi đó các weight cũng gần bằng 0 . Và chúng không update được weight dẫn đến mạng không thể hội tụ được.Vấn đề này được gọi là vanishing gradient và nó đặc biệt nghiêm trọng khi sử dụng activation sigmoid trong các mạng thần kinh sâu. Điều này là do hàm sigmoid có phạm vi giới hạn và có thể dễ dàng bão hòa, khiến gradient trở nên rất nhỏ. Ngược lại, các chức năng kích hoạt khác như ReLU hoặc các biến thể của nó không có giới hạn này và có xu hướng hoạt động tốt hơn trong các mạng thần kinh sâu.

Mặc dù đã có nhiều cải tiến như activation Relu, Elu nhưng ở đây tác giả cho rằng Gelu của chúng tôi tốt hơn nhiều dựa vào khả năng phân phối xác suất để có khả năng sửa đổi thích ứng dropout.Mọi chi tiết bạn có thể tham khảo trên paper của tác giả, tuy nhiên bài viết này sẽ nhằm mở rộng phần phân phối gaussian để các bạn hiểu rõ hơn về chúng.

Phần 2. Tích phân Gaussian

Ta biết được rằng $\phi_{x}$ chính là loss function gaussian. Mục tiêu trong bài viết này chính là chúng , đầu tiên ta sẽ tính toán tích phân của chúng xem chúng hoạt động như nào .

Tuy nhiên chúng không thể tính tích phân như bình thường được. Sẽ có một số tính chất của tích phân gaussian là chúng không phụ thuộc vào trung bình và phương sai điều này có nghĩa mặc kệ phân phối gaussian có là tiêu chuẩn hay không chúng đều sẽ có giá trị trung bình là 0 và phương sai là 1.

Ta sẽ bắt đầu tính tích phân của một gaussian

Trong bài viết này ta sẽ tính tích phân một cách đơn giản và chi tiết nhất, bất cứ ai cũng có thể tính toán ra được. Ta sẽ sử dụng bằng cách gập giấy đễ tính chúng , mặc dù nghe có vẻ hơi buồn cười . Như đã nói giải thích toán học sẽ có rất nhiều cách thức khác nhau và ta sẽ chọn cách thức dễ dàng nhất. Trong cách này chúng ta sẽ sử dụng giải thích chỉ với cấp bậc toán tiểu học. Bằng cách vẽ ra một quả cầu hình chuông chính là gaussian

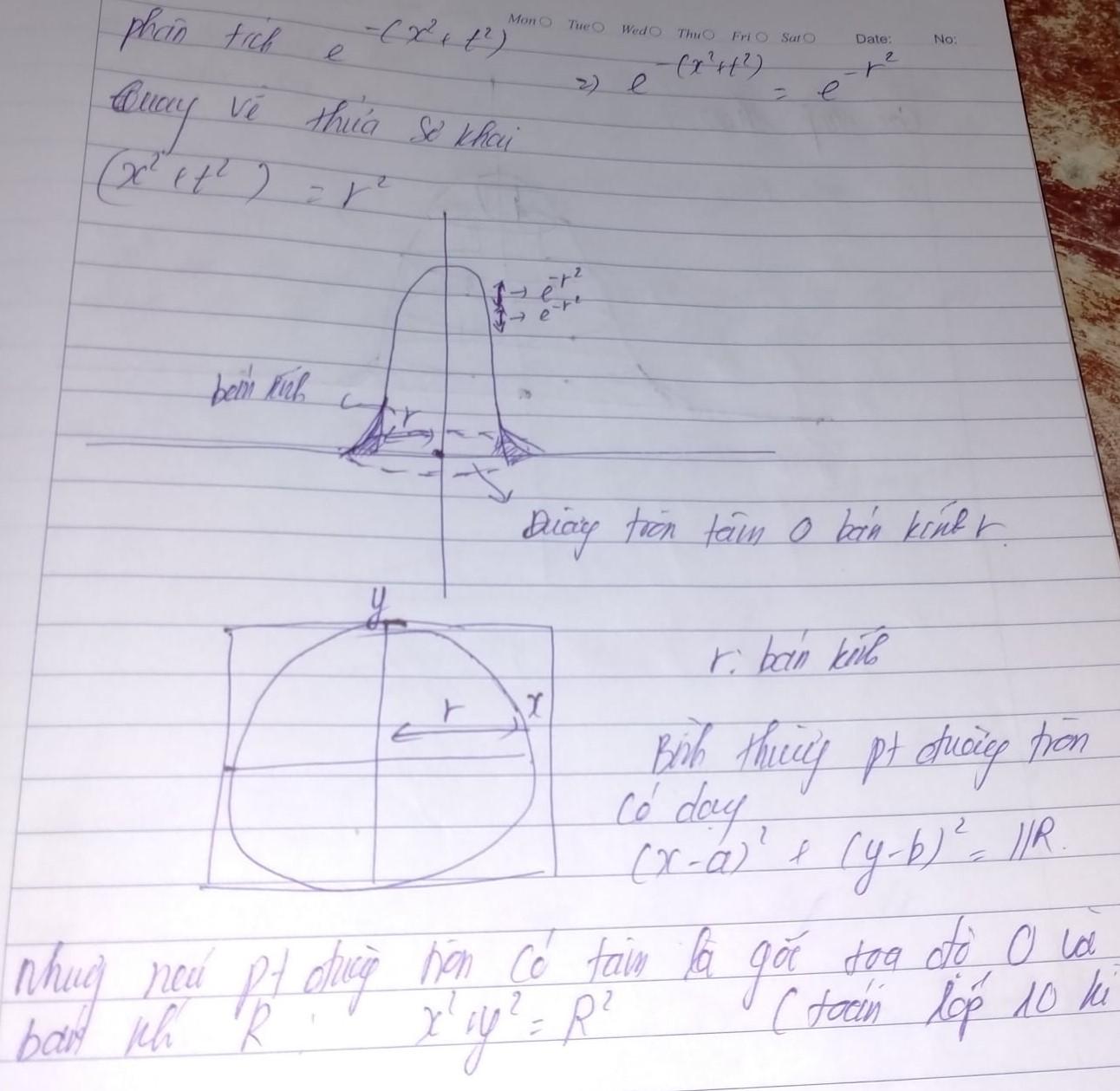
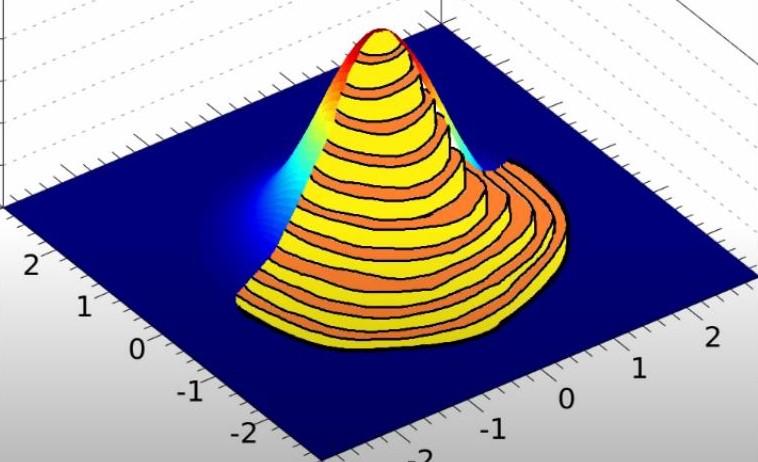
Hình vẽ này chính là phân phối gaussian với mỗi trục đều là một đường tròn có tâm giống nhau tuy nhiên bán kính sẽ thay đổi bé dần theo thời gian. .Để có cái nhìn chi tiết về hình vẽ

Từ hình ảnh trên bạn nhận ra rằng gaussian chính là kết quả của nhiều hình trụ tròn kết hợp lại với nhau mà thành, mặc dù trông hình ảnh không tướng xứng cho lắm nhưng chỉ cần các bạn để ý chút là sẽ nhận ra điều đặc biệt ở đây. Khi cắt giấy hình trụ tròn ta được hình vòng cung trụ và bóp giấy ta sẽ được một hình chữ nhật.

Ta biết được tích phân chính là diện tích của chúng , nên từ định nghĩa của tích phân ta tính ra quy luật hình vẽ như vậy . Hóa ra chúng rất đơn giản , không có thứ gì phức tạp đằng sau bản thân chúng.

Giờ thì hóa ra ta đã hiểu rõ một điều tích phân gaussian chính là căn bậc 2 của $\pi$ .Có một số điều trong bài báo tác giả chưa nói ra tại sao mà hàm lỗi gaussian lại cho ra kết quả của activation tanh. Trong phần này ta sẽ chứng minh toán học giữa chúng với nhau. Tác giả đã dùng định luật này đễ tính sấp sỉ số ra kết quả

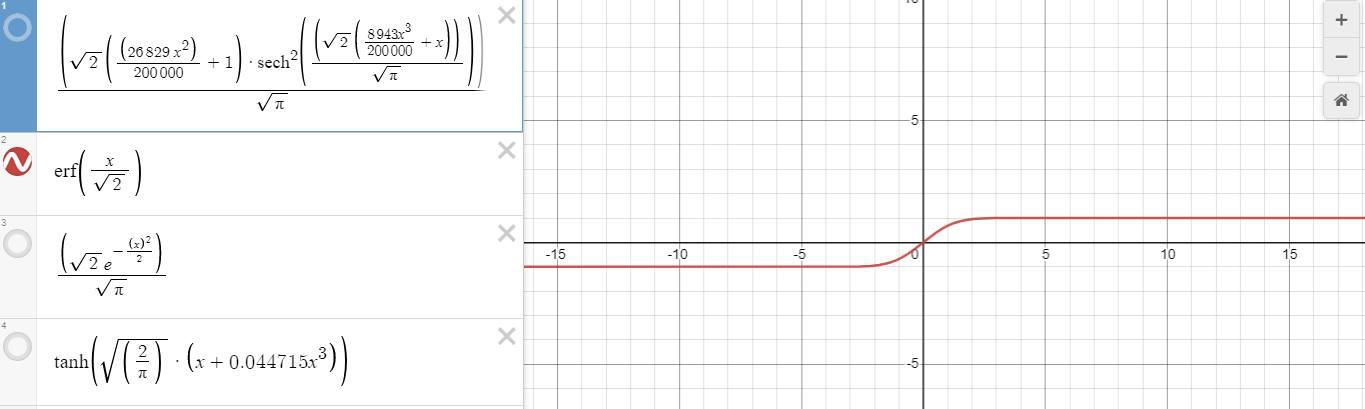
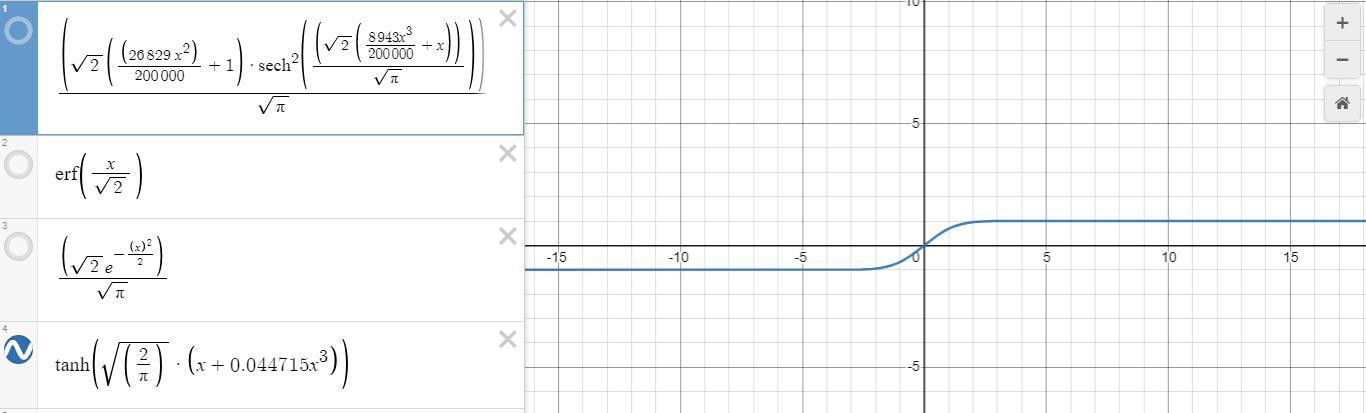
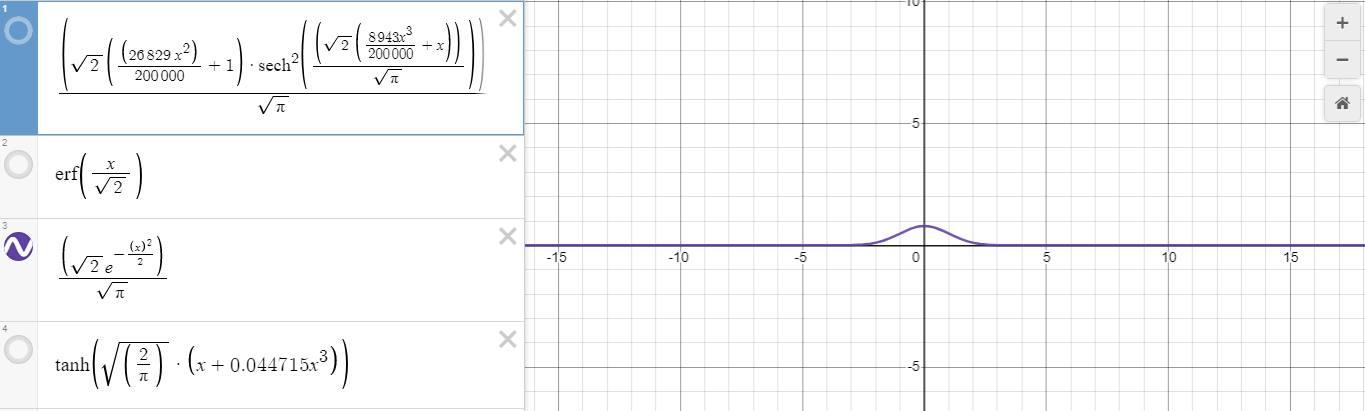
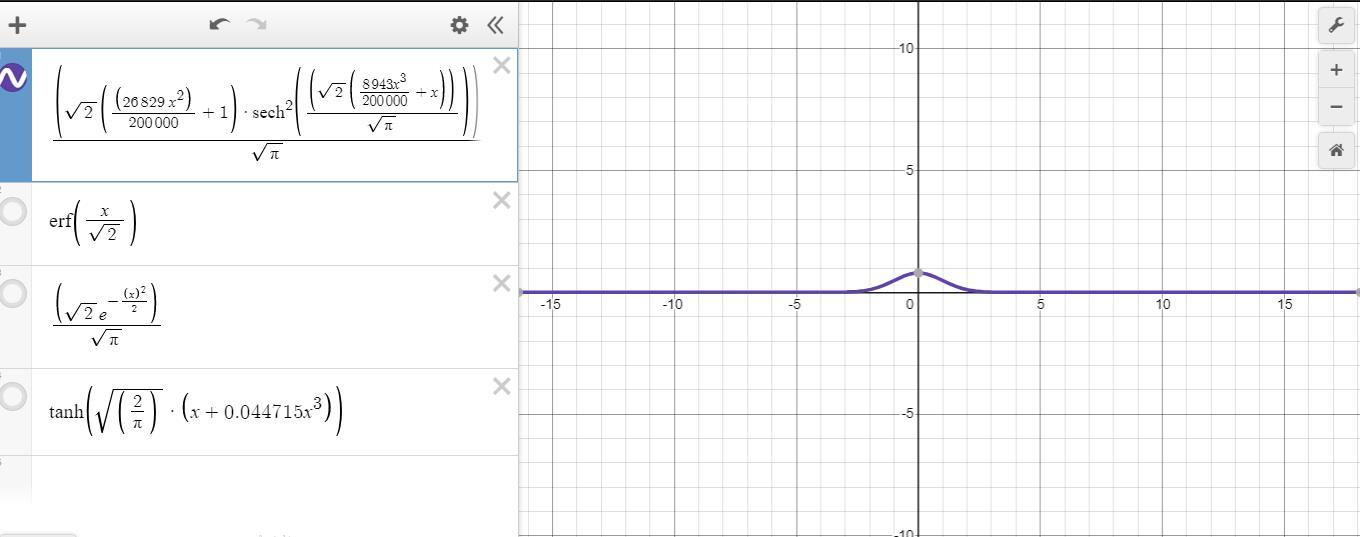
Trên đây là toàn bộ quá trình chúng ta tìm hiểu về tích phân gaussian và giải thích một phần hàm loss gaussian chính là tanh. Tiếp theo ta sẽ dựa vào sơ đồ trên có 2 cách chứng minh hàm loss gausian bằng tanh bằng biểu đồ sơ đồ sử dụng phần mền để vẽ ra . Mong các bạn đã hiểu rõ hơn về chúng

.

Kết hợp cả 2 biểu đồ trên ta nhận định chúng đều có giá trị trong khoảng từ [-1;1] Cùng toàn bộ giá trị với nhau trong suốt biểu đồ này.

Như vậy là chúng ta đã hoàn tất quá trình hiểu sơ lước về phân phối gaussian trong activation gelu. Tiếp theo chúng ta sẽ xem xét đạo hàm giữa chúng với nhau khi backward là như thế nào?

Phần 3. Đạo hàm Gelu

Ở đây chúng ta sẽ gộp tất cả lại rồi tính toán với nhau, đầu tiên sẽ là tính phần Hàm loss gaussian chính là tanh để xem chúng như thế nào?

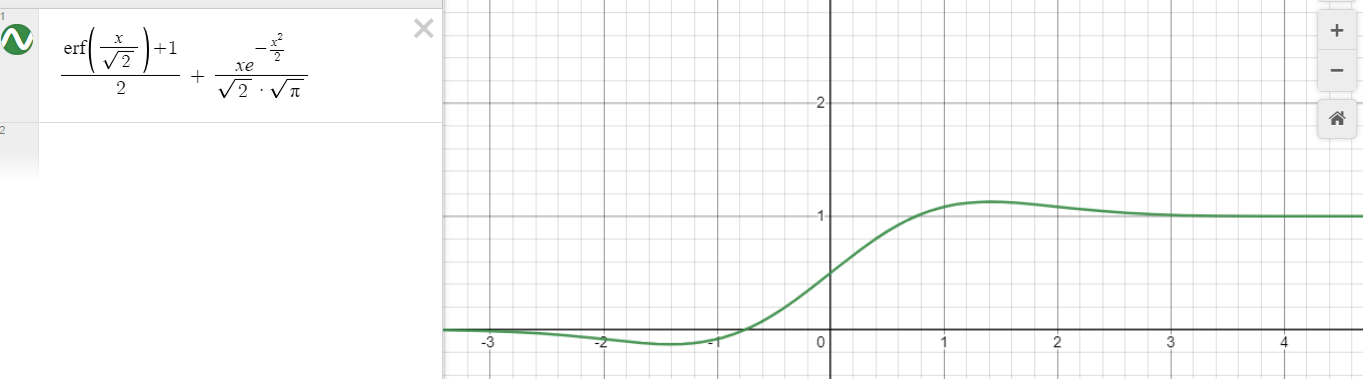
Từ đó ta có thể nhận xét được rằng đạo hàm của erf(x/sqrt2) hay tanh sẽ tạo ra một phân phối chuẩn. Bây giờ chúng ta sẽ bắt đầu tính toán toàn bộ đạo hàm activation function gelu.

$\dfrac{d}{dx}\dfrac{1}{2}x\left(1+\operatorname{erf}\left(\dfrac{x}{\sqrt{2}}\right)\right)$

$=\dfrac{d}{dx}\dfrac{x\cdot\left(\operatorname{erf}\left(\dfrac{x}{\sqrt{2}}\right)+1\right)}{2}$

$=\dfrac{\operatorname{erf}\left(\dfrac{x}{\sqrt{2}}\right)+\dfrac{\sqrt{2}\,x\mathrm{e}^{-\dfrac{x^2}{2}}}{\sqrt{{\pi}}}+1}{2}$

$=\dfrac{\operatorname{erf}\left(\frac{x}{\sqrt{2}}\right)+1}{2}+\dfrac{x\mathrm{e}^{-\frac{x^2}{2}}}{\sqrt{2}\sqrt{{\pi}}}$

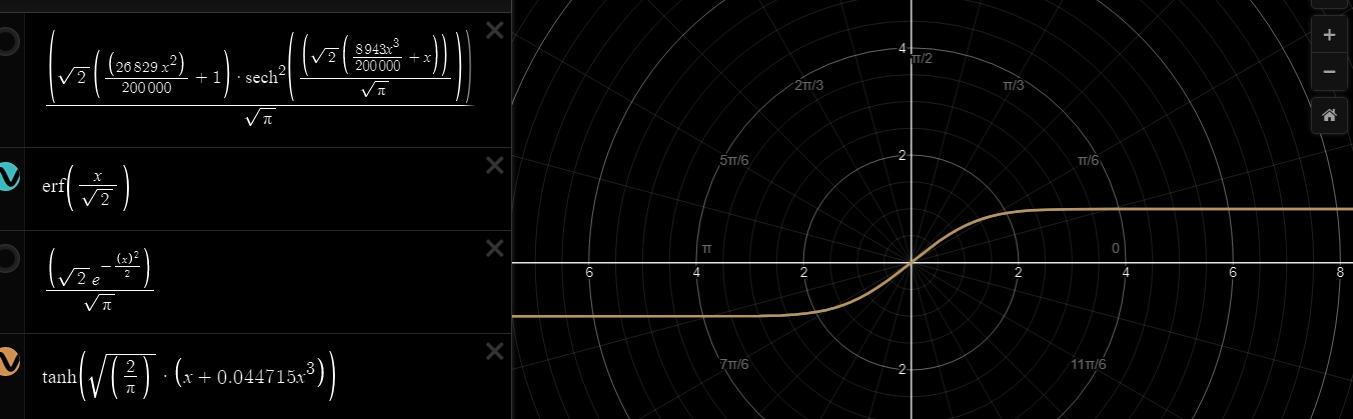
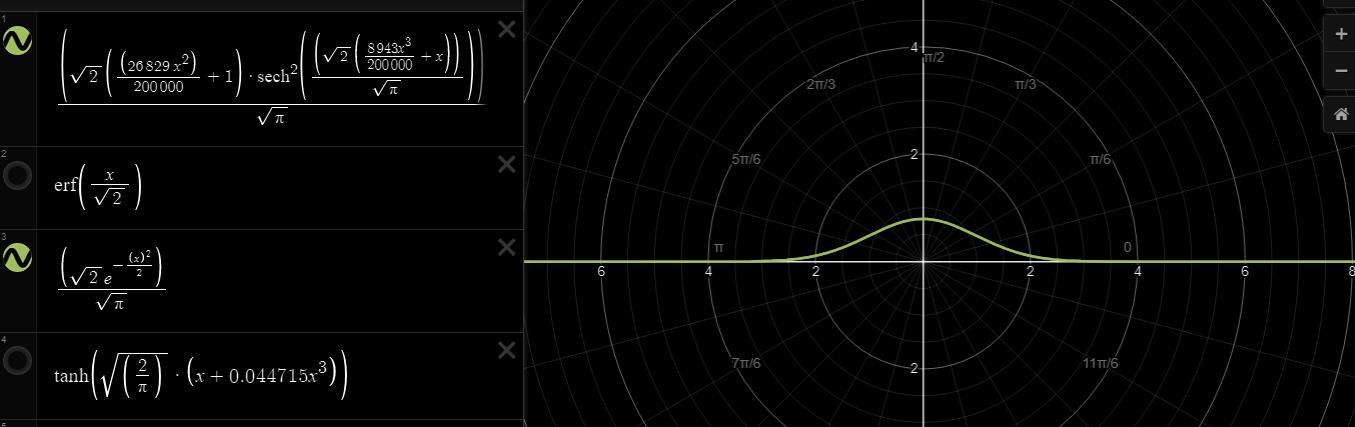
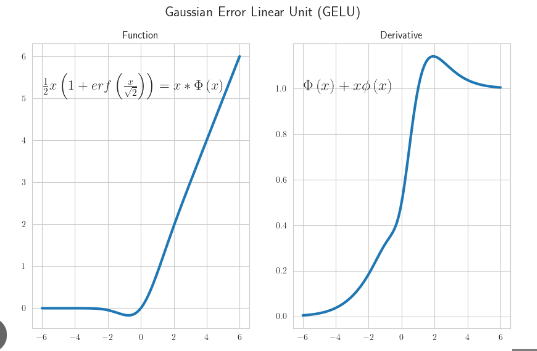
Sơ đồ kết quả hình vẽ khi đạo hàm gelu

Ta nhận ra rằng khi đạo hàm có một số giá trị sẽ vượt qua khỏi 0 và 1 . Hoặc là số âm hoặc dương nhưng khi vượt qua giá trị như vậy tất cả chúng sẽ nằm trong khoảng từ 0 đến 1. Điều đó dẫn đến activation này biết nắm bắt tính linear và tính non linear so với một số activation khác hơn nữa chúng ta nhận thấy rằng đường cong một cách mượt mà hơn. Hãy giả sử như relu chúng bị bó cụ tại giá trị là 0, gelu đã khắc phục điều này. Hơn nữa do giá trị không bị như sigmoid hay tanh nên chúng không bị triệt tiêu gradient . Đây chính là nguyên nhân dẫn đến các model transformers hiện nay mặc dù đào tạo vô số lớp mạng dạy đặc rất sâu nhưng không bị triệt tiêu grdient , chúng luôn hội tụ.