JavaScript Algorithms: Bubble Sort

Bài đăng này đã không được cập nhật trong 5 năm

Introduction

Bubble Sort là một trong những thuật toán sắp xếp đơn giản và phổ biến, được dựa trên việc so sánh từng cặp phần tử liền kề nhau và tráo đổi thứ tự nếu thỏa mãn điều kiện cho trước. Dù Bubble Sort khá đơn giản nhưng tuy nhiên đây là giải thuật chậm nhất trong số các giải thuật sắp xếp cơ bản. Bài viết này sẽ ứng dụng Bubble Sort trong JS và thêm thắt một chút để nó hiệu quả hơn.

Implement

Định nghĩa function:

const bubbleSort = (array) => {
  // stuff will go in here
  return array;
}

Khởi tạo vòng lặp bao ngoài: (outer loop)

const bubbleSort = (array) => {
  for (let i = 0; i < array.length; i++) {
    // more stuff will go in here  
  }
  return array;
}

Thêm vòng lặp con bên trong: (inner loop)

Chúng ta thêm một nested for bên trong để so sánh từng phần tử với các phần tử còn lại trong mảng:

const bubbleSort = (array) => {
  for (let i = 0; i < array.length; i++) {
    for (let x = 0; x < array.length - 1 - i; x++) {
      // even more stuff will go in here
    }
  }
  return array;
}

Compare and Swap

Ở đây sử dụng ES6’s destructuring syntax để thực hiện việc đổi vị trí của các phần tử:

const bubbleSort = (array) => {
  for (let i = 0; i < array.length; i++) {
    for (let x = 0; x < array.length - 1 - i; x++) {
      if (array[x] > array[x + 1]) {
        [array[x], array[x + 1]] = [array[x + 1], array[x]];
      }
    }
  }
  return array;
}

Có thể thấy rằng ở đây trong inner loop, luôn set từ index = 0 đến bất cứ index hiên tại nào của outer loop bên ngoài trừ đi 1. Tức là array.length-1-i sẽ tương đương với array.length-1-0 ở lần thứ nhất của outer loop và array.length-1-1 ở lần lặp thứ hai.. cho đến hết.

Vì cứ sau mỗi lần lặp inner loop, phần tử có giá trị lớn nhất sẽ được dịch chuyển sang bên phải. Điều đó có nghĩa là sau lần lặp đầu tiên, phần tử ở cuối cùng của mảng là phần tử có giá trị lớn nhất, bởi vì phần tử đó đã được so sánh trực tiếp hoặc gián tiếp với các phần tử còn lại trong dãy qua các lần lặp inner loop. Thế nên việc so sánh phần tử đó với các phần tử còn lại thêm lần nữa ở các lần lặp outer loop tiếp theo là không cần thiết.

Giả sử với mảng [9,10,8,7,6,5,4,3,2,1]:

Ở cuối mỗi lần lặp outer loop, mảng hiện tại sẽ ngày càng nhỏ đi:

[9,10,8,7,6,5,4,3,2,1]
[9,8,10,7,6,5,4,3,2,1]
[9,8,7,10,6,5,4,3,2,1]
[9,8,7,6,10,5,4,3,2,1]
[9,8,7,6,5,10,4,3,2,1]
[9,8,7,6,5,4,10,3,2,1]
[9,8,7,6,5,4,3,10,2,1]
[9,8,7,6,5,4,3,2,10,1]
[9,8,7,6,5,4,3,2,1,10]
[8,9,7,6,5,4,3,2,1]
[8,7,9,6,5,4,3,2,1]
[8,7,6,9,5,4,3,2,1]
[8,7,6,5,9,4,3,2,1]
[8,7,6,5,4,9,3,2,1]
[8,7,6,5,4,3,9,2,1]
[8,7,6,5,4,3,2,9,1]
[8,7,6,5,4,3,2,1,9]
[7,8,6,5,4,3,2,1]
[7,6,8,5,4,3,2,1]
[7,6,5,8,4,3,2,1]
[7,6,5,4,8,3,2,1]
[7,6,5,4,3,8,2,1]
[7,6,5,4,3,2,8,1]
[7,6,5,4,3,2,1,8]
[6,7,5,4,3,2,1]
[6,5,7,4,3,2,1]
[6,5,4,7,3,2,1]
[6,5,4,3,7,2,1]
[6,5,4,3,2,7,1]
[6,5,4,3,2,1,7]
[5,6,4,3,2,1]
[5,4,6,3,2,1]
[5,4,3,6,2,1]
[5,4,3,2,6,1]
[5,4,3,2,1,6]
[4,5,3,2,1]
[4,3,5,2,1]
[4,3,2,5,1]
[4,3,2,1,5]
[3,4,2,1]
[3,2,4,1]
[3,2,1,4]
[2,3,1]
[2,1,3]
[1,2]

Trong khi đó mảng mới chứa các phần tử đã được sắp xếp theo thứ tự thì ngày càng lớn hơn:

[]
[]
[]
[]
[]
[]
[]
[]
[]
[10]
[10]
[10]
[10]
[10]
[10]
[10]
[10]
[9,10]
[9,10]
[9,10]
[9,10]
[9,10]
[9,10]
[9,10]
[8,9,10]
[8,9,10]
[8,9,10]
[8,9,10]
[8,9,10]
[8,9,10]
[7,8,9,10]
[7,8,9,10]
[7,8,9,10]
[7,8,9,10]
[7,8,9,10]
[6,7,8,9,10]
[6,7,8,9,10]
[6,7,8,9,10]
[6,7,8,9,10]
[5,6,7,8,9,10]
[5,6,7,8,9,10]
[5,6,7,8,9,10]
[4,5,6,7,8,9,10]
[4,5,6,7,8,9,10]
[3,4,5,6,7,8,9,10]
[1,2,3,4,5,6,7,8,9,10]

Để rút ngắn thời gian, ta có thể chỉ ra khi nào thì mảng đã được sắp xếp hoàn chỉnh tại mỗi thời điểm vòng lặp inner loop kết thúc, nếu không còn gì để sắp xếp, ta sẽ kết thúc cả vòng lặp, tránh được những lần lặp không cần thiết:

const bubbleSort = (array) => {
  let isOrdered;
  for (let i = 0; i < array.length; i++) {
    isOrdered = true;
    for (let x = 0; x < array.length - 1 - i; x++) {
      if (array[x] > array[x + 1]) {
        [array[x], array[x + 1]] = [array[x + 1], array[x]];
        isOrdered = false;
      }
    }
    if (isOrdered) break;
  }
  return array;
}

Ở đây dùng flag isOrdered để phân biệt xem mảng đã sắp xếp xong hay chưa. Flag được set true ở mỗi thời điểm bắt đầu outer loop và sẽ set false ở inner loop mỗi khi cần sắp xếp lại phần tử. Sau khi inner loop kết thúc, nếu không còn gì để sắp xếp, sẽ kết thúc outer loop, trả về kết quả và ngược lại.

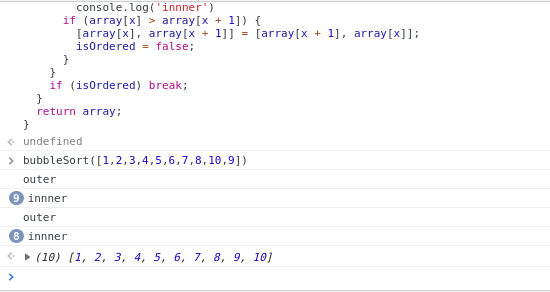
Vd như với mảng [1,2,3,4,5,6,7,8,10,9]:

without flag

Chúng ta cần 45 lần lặp tất cả: