Giới thiệu

Hôm nay mình và các bạn sẽ lại tiếp tục tìm hiểu một loại CTDL mới. Đây là một chủ đề lớn và thú vị. Nó sẽ giới thiệu thêm nhiều loại chủ đề mới đặc biệt khi chúng ta tham gia vào các thuật toán. Chúng được gọi là cây (Tree).
Tất nhiên ý mình không phải cái cây này mà là cái cây bên dưới .

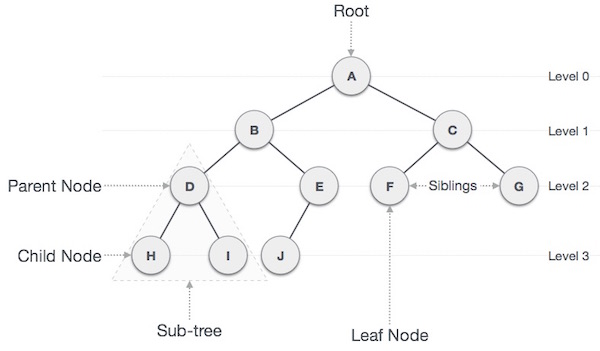
Hình 1

Cây là một loại CTDL có cấu trúc phân cấp, trái ngược với các loại CTDL có cấu trúc tuyến tính mà ta đã học như Arrays hay Hash Tables thường có 0 hoặc nhiều nút con.

Cây bắt đầu bằng một nút gốc hay một nút cha và mọi nút con của cây đi xuống từ nút này. Vì vậy trông nó giống như một cái cây bị đảo ngược. Mọi nút con đều xuất phát từ một nút cha. Các nút cuối không có nút con gọi là lá(leaf).

Một vài ví dụ về cấu trúc dạng cây như là nhận xét trên Facebook, tôi có thể nhận xét về bài đăng của một người bạn, và người bạn đó có thể nhận xét về nhận xét của tôi, hay như ứng dụng của cây vào việc quyết định nước đi khi đánh cờ vua trong học máy ...

Về nguyên tắc, cây cũng sử dụng những liên kết như những gì ta đã biết về Linked List và nó cũng có thể lưu mọi loại dữ liệu tương tự như danh sách liên kết. Và các bạn có thể nghĩ LinkedList cũng là một cây. Và đúng là thế, nó là một loại cây nhưng với chỉ một đường dẫn duy nhất.

Và bây giờ, giống như cuộc sống thực, có rất nhiều loại cây khác nhau như táo, bưởi, cam ... và nếu như chúng ta vào Wikipedia chúng ta cũng có rất nhiều loại CTDL cây khác nhau. Nhưng đừng lo lắng, chúng ta cũng sẽ đi vào một vài loại cây được sử dụng nhiều nhất và các loại cây khác cũng sẽ tương tự chỉ có những khác biệt nho nhỏ và nếu nắm rõ được về Trees, chúng ta sẽ không khó để có thể xử lý được chúng. Let's go.

Các khái niệm cơ bản

• Nút gốc : Là nút trên cùng của cây, nút duy nhất không có nút cha.
• Nút lá : Là các nút có 0 nút con.
• Nút nhánh : Là các nút có cả nút cha và nút con.
• Mức của nút : Là các số nguyên đếm từ 0. Các nút ngang hàng có cùng mức với nhau. Nút gốc có mức là 0, các nút con trực tiếp của gốc có mức là 1 ...
• Chiều cao của cây : Là mức của nút là lớn nhất. Hình 1 thì chiều cao của cây là 3.

Khi bạn đã nắm được những khái niệm này, chúng ta cùng đến với Cây nhị phân.

Binary Trees

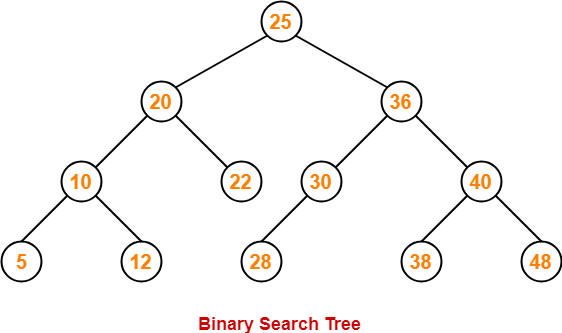
Binary Trees ( cây nhị phân) là một loại cây tương tự như những gì chúng ta đã tìm hiểu ở trên, Tuy nhiên nó có vài quy tắc được áp dụng cho nó nhưng những quy tắc đó khá là đơn giản. Đó là mỗi nút chỉ có thể có 0, 1 hoặc 2 nút con và mỗi nút con chỉ có duy nhất một nút cha.
Một số loại cây nhị phân:

• Cây nhị phân đầy đủ : Mỗi nút trừ nút lá của cây nhị phân đều có 2 nút con.
• Cây nhị phân hoàn hảo : Là cây nhị phân đầy đủ nhưng có thêm điều kiện tất cả nút lá có cùng mức với nhau.
• Cây nhị phân cân bằng : Là cây mà độ chênh lệch giữa nút lá có mức cao nhất và thấp nhất không quá 1.
• Cây nhị phân tìm kiếm : Chúng ta sẽ tìm hiểu tiếp ở phía dưới.

Implement

Implement Node

Để định nghĩa một nút chúng ta cần nhớ mỗi nút sẽ có 1 giá trị và 2 con trỏ để trỏ đến 2 nút con. Ta có thể implement như sau:

class TreeNode<E> {
  final E value;
  TreeNode? left;
  TreeNode? right;

  TreeNode({required this.value, this.left, this.right});
}

Implement Trees.

Để định nghĩa một cây, chúng ta cần quản lý nút gốc. Từ nút gốc chúng ta có thể đi đến những nút con rồi những nút cháu.

class BinarySearchTree {
  TreeNode? root;
}

Tiếp theo chúng ta cùng tìm hiểu về cây nhị phân tìm kiếm(BTS: Binary Search Trees)

Binary Search Trees

Một loại CTDL nổi tiếng nhất là BTS hay còn gọi là cây nhị phân tìm kiếm. Cây nhị phân tìm kiếm là một loại cây nhị phân mà giá trị của các nút con bên trái luôn nhỏ hơn giá trị nút cha và giá trị nút cha luôn nhỏ hơn giá trị của nút con bên phải. Do tính chất này mà cây nhị phân tìm kiếm không được chưa hai phần tử cùng giá trị.

Một cây nhị phân tìm kiếm thực sự tốt khi dùng để tìm kiếm, nó thật tốt khi so sánh mọi thứ. Chúng ta có thể tự hỏi tại sao không sử dụng mảng băm để tìm kiếm, cái mà chúng ta chỉ cần đưa ra key là có thể nhận được giá trị.

Bởi vì BTS là một cấu trúc dữ liệu mà nó bảo trì các mối quan hệ. Ví dụ bạn sẽ không muốn lưu các tệp của máy tính một cách ngẫu nhiên bằng mảng băm, mà chúng ta cần một loại CTDL có tính quan hệ có tính cha con với nhau để làm việc này.

Tiếp theo chúng ta cùng thử thực hiện việc implement một cây nhị phân tìm kiếm để hiểu hơn về nó nhé

Implement

Đầu tiền chúng ta cũng vẫn cần implement một TreeNode và BinarySearchTree có một nút gốc tương tự như Cây nhị phân.

Insert

Tiếp theo chúng ta cùng xem cách thêm một phần tử vào cây nhị phân tìm kiếm. Để thêm một nút vào cây nhị phân tìm kiếm, chúng ta cần tìm được vị trí cho nút mới.
Bắt đầu đi từ gốc xuống chúng ta cần so sánh nút cần thêm với nút hiện tại, nếu lớn hơn thì đi theo bên phải, nhỏ hơn thì đi theo bên trái, đến bao giờ gặp nút lá thì ta thêm vào trái hoặc phải của nút lá tuỳ giá trị so với nút lá.

void insert(int value) {
    final newNode = TreeNode(value: value);
    if (root == null) {
      root = newNode;
    } else {
      var currentNode = root;
      while (true) {
        if (currentNode!.value < value) {
          if (currentNode.right == null) {
            currentNode.right = newNode;
            return;
          } else {
            currentNode = currentNode.right;
          }
        } else {
          if (currentNode.left == null) {
            currentNode.left = newNode;
            return;
          } else {
            currentNode = currentNode.left;
          }
        }
      }
    }
  }

Look up

Việc tìm kiếm thì đơn giản hơn nhiều, ta chỉ việc đi từ trên xuống dưới, so sánh với nút hiện tại nếu lớn hơn thì đi theo nhánh phải, nhỏ hơn thì theo bên trái, nếu gặp thì là tìm thấy.

bool lookup(value) {
    var currentNode = root;
    while (true) {
      if (currentNode == null) {
        return false;
      } else if (currentNode.value == value) {
        return true;
      } else if (currentNode.value < value) {
        currentNode = currentNode.right;
      } else {
        currentNode = currentNode.left;
      }
    }
  }

Remove

Cuối cùng là xoá một nút.
Việc xoá một nút tương đối phức tạp, đòi hỏi nếu nút đó không phải là nút lá thì ta cần tìm một nút thế mạng để thay vào vị trí nút cũ. Để trình bày thì khá mất thời gian và cũng không dễ để hiểu ngay được nên mình sẽ để lại một số công cụ và code của mình để các bạn có thể xem, chạy thử và hiểu được việc này.

• Tool : Một công cụ cho phép bạn làm mọi việc với một BTS để hiểu cách nó vận hành.
• Code

Ưu nhược điểm

• Ưu điểm :
  • Nhìn vào đoạn code trên chúng ta có thể thấy được là BTS có thời gian trung bình cho các hành động là O(logn). Nhanh hơn rất nhiều so với O(n)
  • Có thứ tự
  • Flexible size.
• Nhược điểm là BTS không có bất kì hành động nào có độ phức tạp là O(1).

Và các bạn cũng nên nhớ rằng BTS không phải luôn nhanh nhất, các hành động của BTS luôn có thời gian là trung bình.

Tổng kết

Vậy là qua bài viết này, mình đã giới thiệu đến các bạn về cấu trúc cây, cây nhị phân và cây nhị phân tìm kiếm. Nếu có sai sót hy vọng các bạn góp ý thêm. Cảm ơn các bạn đã theo dõi bài viết, nếu thấy bài viết này hay, đừng quên chia sẻ cho mọi người cùng biết nhé! Cảm ơn các bạn!

Bài tiếp theo: Graphs

Bài trước: Stacks and Queues

Link source code