Continue With Machine Learning - Building Recommendation System

In the last post we explore recommendation system using collaborative filtering by implementing nearest neighbor. In this post we'll try to use matrix factorization on the same data.

Characteristics of Matrix Factorization

The main idea behind matrix factorization is to identify some factors, the so-called hidden factors which influence a user's rating. We identify the factors by decomposing the user item rating matrix into a user-factor matrix and a item-factor matrix.

Each row in the user-factor matrix maps the user onto the hidden factors. These hidden factors (F1, F2, F3, ...) might not have realistic meaning, but they might have abstract meanings which are the factors that determines how the user rate a particular items. Before the factorization is done we have no idea what those factors are. Each row in the item-factor matrix maps the item onto the hidden factors as well.

Matrix factorization is a very expensive operation since it essentially gives us the factors vectors needed to find the rating of any product by any users, whereas for nearest neighbors we only make a computation for 1 user only.

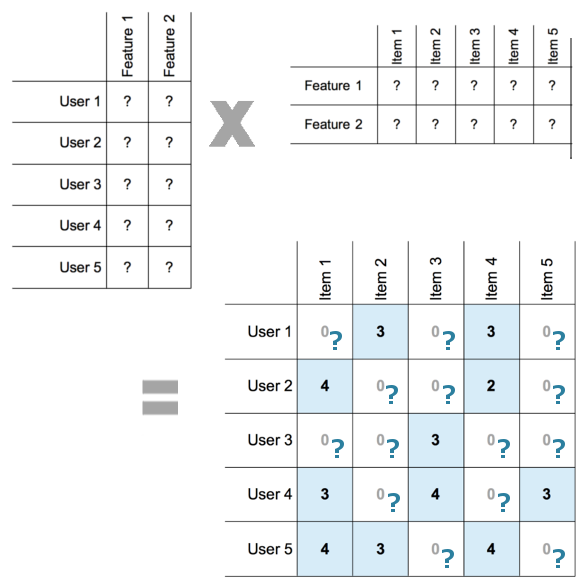
(image from http://katbailey.github.io/post/matrix-factorization-with-tensorflow/ )

One advantage is that we can do one big calculation once, and incrementally update later when needed.

Implementation

To implement matrix factorization we use stochastic gradient descent to minimize the error between prediction and actual rating. To learn the factor vectors (pu and qi), the system minimizes the regularized squared error on the set of known ratings:

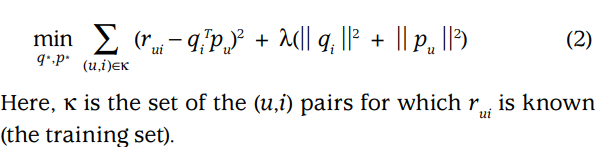
(image from https://datajobs.com/data-science-repo/Recommender-Systems-[Netflix].pdf )

In the last post https://viblo.asia/p/continue-with-machine-learning-building-recommendation-system-Ljy5Vo8jKra we arrive at a userItemRatingsMatrix, which is a pivot table with userId as index and itemId as column and rating as values which look as following:

itemId  1     2     3     4     5     6     7     8     9     10    ...   \
userId                                                              ...    
1        5.0   3.0   4.0   3.0   3.0   5.0   4.0   1.0   5.0   3.0  ...    
2        4.0   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   2.0  ...    
3        NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN  ...    
4        NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN  ...    
5        4.0   3.0   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN  ...    

itemId  1673  1674  1675  1676  1677  1678  1679  1680  1681  1682  
userId                                                              
1        NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN  
2        NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN  
3        NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN  
4        NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN  
5        NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN  

[5 rows x 1682 columns]

Here we'll write a matrix factorization method: We'll be using Stochastic Gradient descent to find the factor vectors.

(picture from https://bigsnarf.wordpress.com/2016/07/16/neural-network-from-scratch-in-python/ )

#Using another method called latent factor matrix factoriazation
def matrixFactorization(userItemRatingsMatrix, numFeatures, numStep=100, gamma=0.01, lamda=0.001):
    # gamma and lamda are parameters for regualization
    numUsers = len(userItemRatingsMatrix.index)
    numItems = len(userItemRatingsMatrix.columns)
    userFactors = pd.DataFrame(np.random.rand(numUsers, numFeatures), index=userItemRatingsMatrix.index)
    # We're initializing this matrix with some random numbers, 
    # then we will iteratively move towards the actual values we want to find
    itemFactors = pd.DataFrame(np.random.rand(numItems, numFeatures), index=userItemRatingsMatrix.columns)
    
    for step in range(numStep):
        # SGD will loop through the ratings of each user on each item as many times
        # as we specify or until the error we are minimizing reaches a certain threshold
        for i in userFactors.index:
            for j in itemFactors.index:
                if userItemRatingsMatrix.loc[i,j] > 0:
                    # For each rating that exists in the training set  
                    eij = userItemRatingsMatrix.loc[i,j] - np.dot(userFactors.loc[i], itemFactors.loc[j])
                    # This is the error between the actual value of the rating 
                    #and the predicted value, that is the dot product
                    # of the corresponding user factor vector and item-factor vector 
                    userFactors.loc[i] = userFactors.loc[i] + gamma * (eij * itemFactors.loc[j] - lamda * userFactors.loc[i])
                    itemFactors.loc[j] = itemFactors.loc[j] + gamma * (eij * userFactors.loc[i] - lamda * itemFactors.loc[j])
                    # userFactors and itemFactors should move in the downward 
                    # direction of the slope of the error at the current point
                    # Gamma is the size of the step we are taking
                    # The value in the brackets is the partial derivative of 
                    # the error function we show above, i.e. the slope.
                    # Lambda is the value of the regularization parameter which 
                    # penalizes the model for the number of factors we are finding.
        print(step)
    
    # At this point we have looped through all the ratings once.
    # Now Let's check the value of the error function to see 
    # if we have reached the threshold at which we 
    # want to stop, else we will repeat the process
    
    e = 0
    for i in userFactors.index:
        for j in itemFactors.index:
            if userItemRatingsMatrix.loc[i,j] > 0:
                e = e + pow(userItemRatingsMatrix.loc[i,j] - 
                np.dot(userFactors.loc[i], itemFactors.loc[j]),2) + 
                lamda * (pow(np.linalg.norm(userFactors.loc[i]), 2) + pow(np.linalg.norm(itemFactors.loc[j]),2))
    
    if e < 0.001:
        break;
    print(e)
        
    return userFactors, itemFactors

Let's do some calcuations:

(userFactors, itemFactors) = matrixFactorization(userItemsRatingMatrix, 3, numStep=50)

Note the function is pretty expensive, on my computer it takes about 4 hours just run 50 steps. Ideally we need to run alot more, thousand of times.

Let's print out some movies:

userId = 5
predictItemsRating = pd.DataFrame(np.dot(userFactors.loc[userId], itemFactors.T), index = itemFactors.index, columns=['rating'])
watchedMovies = userItemsRatingMatrix.loc[userId].loc[userItemsRatingMatrix.loc[userId] > 0].index
predictItemsRating = predictItemsRating.drop(watchedMovies)
predictItemsRating = pd.DataFrame.sort_values(predictItemsRating, ['rating'], ascending=[0])[:5]
topRecommendedMovieTitles = itemData.loc[predictItemsRating.index - 1].movie
print(topRecommendedMovieTitles)

Output

itemId
1239           Ghost in the Shell (Kokaku kidotai) (1995)
319     Paradise Lost: The Child Murders at Robin Hood...
812                          Celluloid Closet, The (1995)
852                                      Braindead (1992)
55                                    Pulp Fiction (1994)
Name: movie, dtype: object

The results are very different from the ones using nearest neighbors. This algorithm need huge computational power to produce a good result.