Những câu hỏi mình thường hỏi ứng viên khi phỏng vấn AI - Phần 1 - Lý thuyết toán cơ bản
Bài đăng này đã không được cập nhật trong 6 năm
Xin chào các bạn, song song vơi series Handbook Computer Vision with Deep Learning mình tạo thêm một series nữa về vấn đề những câu hỏi thường hỏi ứng viên khi đi phỏng vấn vào các vị trí AI Engineer. Mình nghĩ đây là một trong những tài liệu hữu ích cho những bạn ứng viên và cả những bạn tham gia phỏng vấn nữa. Bài viết này sẽ giới thiệu đến các bạn các câu hỏi liên quan đến lý thuyết toán học cơ bản mà mình thường hay hỏi khi đi phỏng vấn. Mình xin được tổng hợp lại và chia sẻ cho các bạn. OK, mục đích đã rõ ràng rồi, chúng ta bắt đầu thôi nhé.
1.1 Phân biệt scalars, vectors, ma trận, và tensors?
Đây là một câu hỏi thuộc vào hàng basic nhất. Các bạn đã từng làm qua các framework về Deep learning chắc sẽ không lạ lẫm gì với các khái niệm này.
Scalar
Scalar hay còn gọi là vô hướng hay là một điểm trong hình học. Nó biểu diễn một số trong đại số tuyển tính và khác với hầu hết các đại lượng khác trong đại số tuyển tính (thường là một mảng nhiều số hay vector).
Vector
Một vectơ có thể coi là một tập hợp có quan tâm đến thứ tự (ordered numbers) và thường được biểu diễn bằng một chữ in thường. Ví dụ vectơ trong đó là phần tử đầu tiên của vecto . là phần tử thứ hai của vecto .
Matrix
Tiếng việt còn gọi là ma trận là một tập hợp các vecto có cùng kiểu và số chiều và được biểu diễn bởi một mảng hai chiều. Chúng ta có thể tưởng tượng nó giống như một bảng dữ liệu có tên trường và các giá trị của chúng tương ứng với từng bản ghi trong cơ sơ dữ liệu. Trong đó, một đối tượng được biểu diễn dưới dạng một hàng (row) trong ma trận và một đặc trưng được biểu diễn dưới dạng cột (column). Tại mỗi đối tượng có một giá trị số. Tên của một biến chữ hoa thường được đặt cho ma trận in đậm, chẳng hạn như .
Tensor
Tensor là một khái niệm xuất hiện khá nhiều khi học Machine Learning đặc biệt là lĩnh vực Deep Learning. Nó thực chất có thể hiểu là một đối tượng tương tự như ma trận nhưng với số chiều lớn hơn 2. Nói chung, các phần tử trong một mảng được phân phối trong một không gian có tọa độ nhiều chiều, mà chúng ta gọi là một tensor. Framework khá phổ biến chúng ta hay sử dụng đó là Tensorflow tức là tính toán dựa trên các Tensor. Chúng ta sử dụng để kí hiệu cho tenor . Phần tử có tọa độ trong tensor được ký hiệu là .
Mối quan hệ giữa các đại lượng trên
Chúng ta có thể hình dung các mối quạn hệ này giống như việc bạn đang cầm một cây gậy:
- Scalar là chiều dài của cây gậy, nhưng bạn sẽ không biết cây gậy đang chỉ vào đâu.
- Vector không chỉ biết chiều dài của cây gậy, mà còn biết cây gậy chỉ vào mặt trước hay mặt sau.
- Tensor như một tập hợp của nhiều cây gậy không chỉ biết chiều dài của cây gậy, mà còn biết cây gậy đó đó chỉ về phía trước hay phía sau, và bao nhiêu cây gậy bị lệch lên / xuống và trái / phải.
1.2 Chuẩn norm của vecto và ma trận là gì?
Khi học về Machine Learning hoặc thiết kế các dạng mạng nơ ron chúng ta thường hay nhắc đến các khai niệm về regular là một hình thức để chuẩn hóa theo các norm như norm 1, norm 2, norm p. Câu hỏi này có thể kiểm tra được kiến thức của ứng viên về các khái niệm trong đại số tuyển tính.
Vector norm là gì?
Chúng ta định nghĩa một vecto như sau . Một tập hợp bất kì của các số sẽ đại diện cho một vector. Các chuẩn của viector được định nghĩa như sau:
- Chuẩn 1 - norm 1 của một vector là tổng các giá trị tuyệt đối của các phần tử của vectơ. Ví dụ đối với vector kể trên có norm 1 là 29. Nó được biểu diễn theo công thức toán học sau:
- Chuẩn 2 - norm 2 của một vector là căn bậc hai của tổng bình phương của mỗi phần tử của vectơ. Ví dụ đối với vector kể trên có norm 2 là 15. Nó được biểu diễn theo công thức toán học sau:
- Chuẩn giới hạn âm - negative infinite norm của một vecto là giá trị tuyệt đối nhỏ nhất trong số các phần tử của vector. Được định nghĩa như sau:
- Chuẩn giới hạn dương - positive infinite norm ngược lại với chuẩn giới hạn âm là giá trị tuyệt đổi lớn nhất trong số các phần tử của vecto. Nó được định nghĩa như sau:
- Chuẩn p - norm p của một vector được định nghĩa một cách tổng quát như sau:
Norm của ma trận là gì? Giải thích rõ về chuẩn 1 và chuẩn 2 của ma trận.
Định nghĩa một ma trận một ma trận tùy ý khác có thể định nghĩa bằng công thức trong đó các phần tử là .
Chúng ta định nghĩa các norm của ma trận này như sau:
Norm của ma trận phụ thuộc vào mỗi vecto thành phần của ma trận đó. Chúng ta cũng có một vài chuẩn của ma trận tương tự như vector nhưng cách tính thì sẽ có khác một chút. Cụ thể như sau:
- Chuẩn 1 - norm 1 của một ma trận được tính toán như sau. Các giá trị tuyệt đối của các phần tử trên mỗi cột của ma trận được tính tổng trước sau đó lấy ra giá trị lớn nhất của nó chúng ta sẽ thu được chuẩn 1 của ma trận. Ví dụ như đối với ma trận phía trên chúng ta có các số sau khi cộng tổng giá trị tuyệt đối trên từng cột là và giá trị lớn nhất của nó là 9. Vậy nên norm 1 của ma trận là 9. Chúng ta có công thức tổng quát như sau
- Chuẩn 2 - norm 2 của ma trận được tính toán bằng căn bậc hai của giá trị riêng lớn nhất của ma trận ví dụ đối với ma trận phía trên thì giá trị của norm 2 là 10.0623. Chúng ta có công thức tổng quát cho trường hợp này như sau:
trong đó là giá trị tuyệt đối lớn nhất của giá trị riêng ma trận
1.3 Đạo hàm là gì?
Khi các bạn tiếp cận với các phương pháp Machine Learning dựa trên sự tối ưu hóa một hàm mất mát nào đó thì chắc chắn chúng ta cần phải động đến đạo hàm. Vì vậy các khái niệm cơ bản về đạo hàm chúng ta cũng nên đề cập đến trong khi phỏng vấn.
Đạo hàm được định nghĩa là giới hạn nếu có của tỷ số giữa mức độ thay đổi của hàm số và mức độ thay đổi của đối số tại điểm .
hoắc
Ý nghĩa hình học của đạo hàm là hệ số góc của tiếp tuyến với hàm số tại điểm tiếp xúc.

1.4 Trị riêng và vecto riêng là gì? Nêu một vài tính chất của chúng.
Đây cũng là hai khái niệm tính toán trên ma trận được học trong chương trình đại số tuyến tính thời đại học. Chúng ta cũng có thể trao đổi trong qúa trình phỏng vấn:
Xét ma trận vuông cấp trên trường số . Số được gọi là giá trị riêng của ma trận nếu tồn tại một vector sao cho . Khi đó thì vecto được gọi là vecto riêng của ma trận
Có một vài tính chất của trị riêng và vecto riêng cần lưu ý như sau:
- Giá trị riêng \lamda chính là nghiệm của phương trình đặc trưng của ma trận
- Một giá trị riêng thì có thể có nhiều vector riêng
- Một vector riêng chỉ ứng với một giá trị riêng duy nhất
- Ma trận A là nghiệm của đa thức đặc trưng của chính nó (trong trường hợp này đa thức đặc trưng được coi là đa thức ma trận, nghĩa là biến số của nó không phải là biến số thực mà là biến ma trận)
- Nếu là giá trị riêng của ma trận A thì A không khả nghịch. Ngược lại, nếu mọi GTR của A đều khác không thì A khả nghịch.
- Nếu là giá trị riêng của thì cũng là giá trị riêng của
1.5 Xác suất là gì? Tại sao nên sử dụng xác suất trong machine learning?
Xác suất của một biến cố (event) là một đại lượng để đo khả năng xuất hiện của sự kiện đó. Sự xuất hiện của một sự kiện trong một thử nghiệm ngẫu nhiên là ngẫu nhiên, các thử nghiệm ngẫu nhiên có thể được lặp lại với số lượng lớn trong cùng điều kiện có xu hướng thể hiện các mô hình xác suất của sự kiện đó. Ngoài việc đối phó với những điều không chắc chắn, machine learning cũng cần phải đối phó với số lượng ngẫu nhiên. Sự không chắc chắn và ngẫu nhiên có thể đến từ nhiều nguồn, sử dụng lý thuyết xác suất để định lượng độ tin cậy của một mô hình machine learning. Lý thuyết xác suất đóng vai trò trung tâm trong học máy vì việc thiết kế các thuật toán học máy thường dựa vào các giả định xác suất về dữ liệu.
Chẳng hạn, trong khóa học về Machine Learning của (Andrew Ng), có một giả thuyết Naive Bayes là một ví dụ về sự độc lập có điều kiện. Thuật toán huấn luyện được đưa ra dựa trên nội dung để xác định xem email có phải là thư rác hay không. Giả sử rằng điều kiện xác suất mà từ x xuất hiện trong tin nhắn là độc lập với từ y, bất kể tin nhắn đó có phải là thư rác hay không. Rõ ràng giả định này không phải là không mất tính tổng quát, bởi vì một số từ hầu như luôn luôn xuất hiện cùng một lúc. Tuy nhiên, kết quả cuối cùng là giả định đơn giản này ít ảnh hưởng đến kết quả và trong mọi trường hợp cho phép chúng ta có thể nhanh chóng xác định thư rác.
:max_bytes(150000):strip_icc()/GettyImages-122143117-5c64996246e0fb0001f256b1.jpg)
1.6 Biến ngẫu nhiên là gì? Nó khác gì so với biến đại số thông thường?
Trên thực tế, với một hàm số có thể cho các kết quả khác nhau trong một biến cố ngẫu nhiên (hay nói cách khác một hiện tượng không phải lúc nào cũng xuất hiện cùng một kết quả trong các điều kiện nhất định). Ví dụ, số lượng hành khách chờ tại trạm xe buýt tại một thời điểm nhất định, số lượng cuộc gọi mà tổng đài điện thoại nhận được tại một thời điểm nhất định, v.v., đều là ví dụ về các biến ngẫu nhiên. Sự khác biệt của biến ngẫu nhiên so với một biến đại số thông thường đó chính là xác suất. Khi xác suất giá trị của một biến không phải là 1 (nhỏ hơn 1) thì một biến đại số thông thường trở thành biến ngẫu nhiên. Nếu một biến ngẫu nhiên có xác suất xuất hiện giá trị là 1 thì nó trở thành biến đại số thông thường.
Ví dụ: Khi xác suất của biến có giá trị 100 là 1, thì được xác định và sẽ không thay đổi tức là nó là biến đại số thông thường. Khi xác suất của biến có giá trị là 50 là 0,5 và và xác suất đẻ có giá tị là 100 là 0,5. Tức là gái trị của biến sẽ thay đổi với các điều kiện khác nhau. Đó là một biến ngẫu nhiên.
1.7 Xác suất có điều kiện là gì? Cho ví dụ?
Một xác suất có điều kiện thường có công thức như sau:
Chúng ta có thể giải thích xác suất có điều kiện như sau
Đối với sự kiện hay tập hợp con và thuộc vào cùng một không gian mẫu . Nếu như một phần tử được lựa chọn ngẫu nhiên từ thuộc về thì trong lần lựa chọn ngẫu nhiên tiếp theo, xác suất thuộc về được xác định là xác suất có điều kiện của với tiền đề là . và kí hiệu như sau
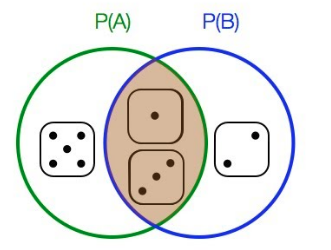
Theo sơ đồ Venn, có thể thấy rõ rằng trong trường hợp sự kiện B, xác suất xảy ra sự kiện A là chia cho .
Ví dụ về xác suất có điều kiện thì có thể rất dễ dàng lấy được trong cuộc sống.
Ví dụ: Một cặp vợ chồng sinh đôi. Xác suất mà một trong số họ là con gái và người còn lại cũng là con gái là gì? (Mình đã từng hỏi ứng viên câu này trong các cuộc phỏng vấn và nó cũng được xuất hiện trong bài kiểm tra môn xác suất thống kê thời địa học)
1.8 Khái niệm về kỳ vọng, phương sai và ý nghĩa của chúng?
Kì vọng - Expectation
Trong lý thuyết xác suất và thống kê, kỳ vọng toán học (hay trung bình, còn được gọi là kỳ vọng) là tổng xác suất của mỗi kết quả có thể có trong thử nghiệm nhân với kết quả. Nó phản ánh giá trị trung bình của các biến ngẫu nhiên. Kì vọng có một số tính chất sau:
- Kì vọng của một tổng bằng tổng của các kì vọng
- Hay chúng ta có thể viết dưới dạng tổng quát:
- với là một hằng số
- với là các hằng số
- với là các biến độc lập
- Với kì vọng của hàm số chúng ta có thể chia thành hai trường hợp
- Với hàm số rời rạc:
- Với hàm số liên tục:
Phương sai - Variance
Dựa vào kì vọng ta sẽ có được trung bình của biến ngẫu nhiên, tuy nhiên nó lại không cho ta thông tin về mức độ phân tán xác suất nên ta cần 1 phương pháp để đo được độ phân tán đó. Một trong những phương pháp đó là phương sai (variance). Phương sai là trung bình của bình phương khoảng cách từ biến ngẫu nhiên tới giá trị trung bình. Chúng ta có thể xem xét công thức tổng quát của phương sai như sau:
Tuy nhiên, Việc tính toán dựa vào công thức này khá phức tạp, nên trong thực tế người ta thường sử dụng công thức tương đương sau:
Chúng ta có thể thấy rằng phương sai luôn là một giá trị không âm và phương sai càng lớn thì nó thể hiện mức độ phân tán dữ liệu càng rộng hay nói cách khác mức độ ổn định càng nhỏ.
Kết luận
Trên dây là một số câu hỏi về toán cơ bản chúng ta có thể sử dụng để kiểm tra ứng viên trong các kì phỏng vấn về AI. Rất mong được sự góp ý bổ sung của các bạn để hoàn thiện hơn nữa series này.
All rights reserved
