Ý nghĩa của tên gọi "Cross-Entropy"

Giới thiệu

Chắc hẳn các bạn không còn xa lạ gì với các mô hình ngôn ngữ lớn (large language models - LLM), kể từ khi OpenAI ra mắt ChatGPT vào tháng 11 năm ngoái (2022) thì thuật ngữ này ngày càng xuất hiện nhiều hơn và AI cũng được chú ý đến nhiều hơn. Sau hơn 1 năm số lượng các mô hình ngôn ngữ gia tăng một cách chóng mặt với đa dạng về kích thước, ngôn ngữ, phạm vi ứng dụng. Có thể nói lĩnh vực này đang trở nên nóng hơn bao giờ hết.

Các LLM này tuy đa dạng nhưng lại có một điểm chung đó là đều sử dụng kiến trúc Transformer. Và lớp cuối cùng của các mô hình này đều là một lớp Linear(hay còn gọi là Fully Connected) kết hợp với Softmax. Output của các mô hình LLM này có phải rất giống output của các mô hình phân loại (Classification models) đúng không nào, và Cross-Entropy là làm loss được sử dụng thường xuyên trong các mô hình phân loại (chúng cũng có thể được sử dụng để huấn luyện các mô hình LLM, tuy nhiên ngày nay có nhiều kỹ thuật cho độ chính xác cao hơn).

Trong bài viết này hãy cùng mình tìm hiểu kỹ hơn một chút về Cross-Entropy Loss, nó là gì, nó được xây dựng như thế nào và tại sao nó lại được sử dụng nhiều trong Machine Learning.

Hãy cùng bắt đầu từ tên gọi của nó. Đã bao giờ các bạn tự hỏi tại sao nó lại được gọi là Cross-entropy chưa? Trong khi công thức của nó thì như này:

$$H(y, \hat{y}) = -\sum_{i} y_i \log(\hat{y}_i) \tag{1}$$

Trong đó:

• $y$ là vector biểu diễn nhãn thực tế (ground truth) trong định dạng one-hot encoding. Nghĩa là $y_i$ bằng 1 cho nhãn đúng và 0 cho tất cả các nhãn khác.
• $\hat{y}$ là vector biểu diễn xác suất dự đoán của mô hình cho mỗi lớp.
• $y_i$ là giá trị thực tế của nhãn thứ $i$ trong vector $y$.
• $\hat{y}i$ là xác suất dự đoán cho nhãn thứ $i$ trong vector $\hat{y}$.
• Tổng sum $\sum_{i}$ được thực hiện trên tất cả các lớp.

Và đây là công thức của Entropy thông tin (theo định nghĩa của Claude Shannon). Entropy thông tin đo lường lượng "bất định" hoặc "sự không chắc chắn" trong thông tin, hay nói cách khác, là một cách đo lường thông tin trung bình mà một biến ngẫu nhiên mang lại (Chúng ta sẽ tìm hiểu ở phần sau):

$$H(X) = -\sum_{i=1}^{n} P(x_i) \log_b P(x_i) \tag{2}$$

Trong công thức này:

• $H(X)$ là entropy của biến ngẫu nhiên $X$.
• $n$ là số lượng các kết quả có thể xảy ra của $X$
• $P(x_i)$ là xác suất $X=x_i$
• $log_b$ là logarit cơ số $b$, thường là 2(logrit nhị phân) trong lý thuyết thông tin, cũng có thể sử dụng cơ số $e$(logarit tự nhiên) hoặc cơ số 10.

Hmmmm🤔. Có vẻ 2 công thức hơi liên quan đến nhau rồi nhỉ. Cùng có logarit của một xác suất nhân với một giá trị xác suất (có thể coi xác suất của nhãn đúng trong ground truth là 1 và nhãn sai là 0). Sau đó lấy tổng trên tất cả các khả năng và thêm dấu $-$. Sự khác nhau duy nhất đó là trong Cross-Entropy thì có 2 giá trị xác suất đó là của nhãn và của mô hình dự đoán. Có lẽ vì thế mà chúng được gọi là Cross hay chéo. Hãy cùng tìm hiểu kỹ hơn để kiểm chứng nhận định này nhé.

I. Cross-Entropy trong lý thuyết thông tin

Để hiểu Cross-Entropy trước tiên chúng ta cần hiểu Entropy là gì. Theo wikipedia thì:

Entropy thông tin mô tả mức độ hỗn loạn trong một tín hiệu lấy từ một sự kiện ngẫu nhiên. Nói cách khác, entropy cũng chỉ ra có bao nhiêu thông tin trong tín hiệu, với thông tin là các phần không hỗn loạn ngẫu nhiên của tín hiệu.

Thật khó hiểu nhỉ Vậy thì hãy cùng xem tiếp nhé

2.1 Thông tin là gì? Cách biểu diễn thông tin trong máy tính. Entropy thông tin

Nếu các bạn tìm định nghĩa thông tin trên internet sẽ ra rất nhiều kết quả mà có thể đọc sẽ chẳng hiểu gì 😩 Mình thì hiểu đơn giản thông tin là những gì mà con người có thể nhận thức được: từ những thứ cụ thể như âm thanh, hình ảnh, nhiệt độ, độ sáng đến những thứ trừu tượng như ngôn ngữ, cảm xúc, giá trị,...

Không phải bất kỳ thông tin nào cũng có thể biểu diễn trong máy tính tạo thành dữ liệu, phổ biến nhất là hình ảnh, âm thanh và văn bản. Những thông tin này được lưu trữ trong máy tính dưới dạng một chuỗi các bits theo một quy tắc nhất định. Và một điểm chung là đều phải lượng tử hóa thông tin và mã hóa mỗi giá trị lương tử bằng một chuỗi bits. Chúng ta sẽ không đi sâu tìm hiểu phần này mà hãy cùng quan tâm đến một loại dữ liệu đơn giản: văn bản

Văn bản hay có thể hiểu là một chuỗi các ký tự có trong một bảng chữ cái hữu hạn nào đó (lương tử hóa). Và mỗi một ký tự sẽ được biểu diễn dưới dạng một chuỗi các bits 0 và 1. Ví dụ như bảng chữ cái tiếng Việt có 29 chữ cái, mỗi chữ cái có thể biểu diễn bằng 8 bits (utf-8) hoặc 16 bits(utf-16).

Để đơn giản nhưng vẫn khái quát, Hãy xét một bảng chữ cái gồm 4 chữ A, B, C và D. Dễ thấy chúng ta chỉ cần 2 bits để có thể biểu diễn hết các ký tự trong bảng chữ cái này như sau:

A: 00, B: 01, C: 10, D: 11

Khi biểu diễn một văn bản tạo thành từ bảng chữ cái trên trong máy tính ta được một chuỗi bits. Ví dụ như chuỗi ABCD sẽ là 00011011, nếu chỉ nhìn chuỗi bits thì con người khó có thể hiểu được đúng không nào. Vì vậy để giải mã lại chuỗi bits này trở lại thành văn bản sẽ cần đến quá trình giải mã: Đầu tiên tách chuỗi bits thành các cặp 2 bits (có thể nhiều hơn 2 nếu cần nhiều bits hơn để biểu diễn 1 ký tự) gọi là code word. Sau đó dựa vào bảng mã hóa ở trên để giải mã.

00011011 -> 00 01 10 11 -> A B C D

Okay. Bây giờ quay trở lại những năm trước 2012 khi mà điện thoại 2G vẫn còn phổ biến, và 2 nhân vật huyền thoại trong các câu chuyện về an toàn thông tin: Alice và Bob muốn nhắn tin cho nhau sử dụng bảng chữ cái trên, giá cước tin nhắn lúc này là 1đ/bit. Vậy thì trung bình họ cần trả bao nhiêu tiền cho một ký tự? Thật dễ dàng để tính ra được là 2đ/ký tự đúng không nào.

Chuyện không có gì để nói nếu như các nhà cung cấp mạng tăng giá cước nhắn tin lên 10đ/bit. Như vậy chi phí để nhắn tin bây giờ đã tăng lên 20đ/ký tự, gấp 10 lần. Alice và Bob quyết định tìm cách giảm chi phí nhắn tin bằng cách giảm số bit truyền đi. Điều này thực hiện như thế nào???

Đầu tiên, Bob nhận thấy tần suất các ký tự mà Alice dùng để nhắn cho mình không đều nhau, chữ A xuất hiện nhiều nhất (50%), sau đó đến B(25%) và cuối cùng là C và D bằng nhau và bằng 12.5%. Như vậy Alice và Bob có thể lựa chọn cách mã hóa với độ dài codeword cho mỗi ký tự khác nhau là khác nhau, ví dụ như:

A: 0, B: 10, C: 110, D: 111

Dẫn đến cách giải mã cũng sẽ phải khác: Sẽ xét từ bit đầu tiên đến bit cuối cùng, nếu gặp một tổ hợp bits có trong bảng mã hóa thì sẽ giải mã ký tự tương ứng.

Với cách này thì số bit trung bình cần sử dụng là bao nhiêu? Sử dụng công thức tính giá trị trung bình:

$$E(X) = \sum_{X} x \cdot P(X)$$

Trong đó $P(X)$ là xác suất của ký tự $X$ có số lượng bit trong codeword là $x$.

Với cách mã hóa mới thì $E(X) = 0.5 * 1 + 0.25 * 2 + 0.125 * 3 * 2 = 1.75$. Vậy chi phí trung bình cho một ký tự chỉ còn 17.5đ/ký tự. Không giảm là bao nhưng có còn hơn không mà.

Vậy câu hỏi đặt ra là làm sao mà Alice và Bob có thể tìm ra được cách mã hóa nào tối ưu và tính toán được chi phí mà mình phải bỏ ra? Một cách dễ nhận ra đó là dùng codeword có độ dài ngắn hơn cho ký tự xuất hiện với tần suất cao và codeword dài cho ký tự xuất hiện ít. Sau đó tính toán chi phí bằng công thức tính trung bình ở trên.

Câu hỏi tiếp theo là tại sao lại phải mã hóa B với 2 bits, C và D bằng 3 bits? Nguyên nhân cho việc này đến từ sự "nhập nhằng" khi giải mã, nghĩa là từ một chuỗi bits có thể có nhiều văn bản giải mã thỏa mãn. Ví dụ như nếu mã hóa C bằng 01, thì khi gặp chuỗi 010 sẽ có 2 chuỗi thỏa mãn là AB và CA. Vậy phải tạo bộ codeword như thế nào? Câu trả lời là không tạo codeword là tiền tố (prefix) của codeword khác. Ví dụ nếu lấy A là 0 thì không được lấy C là 01 vì có tiền tố 0 đã được gán cho A. Để rõ hơn thì hãy cùng xét bảng sau:

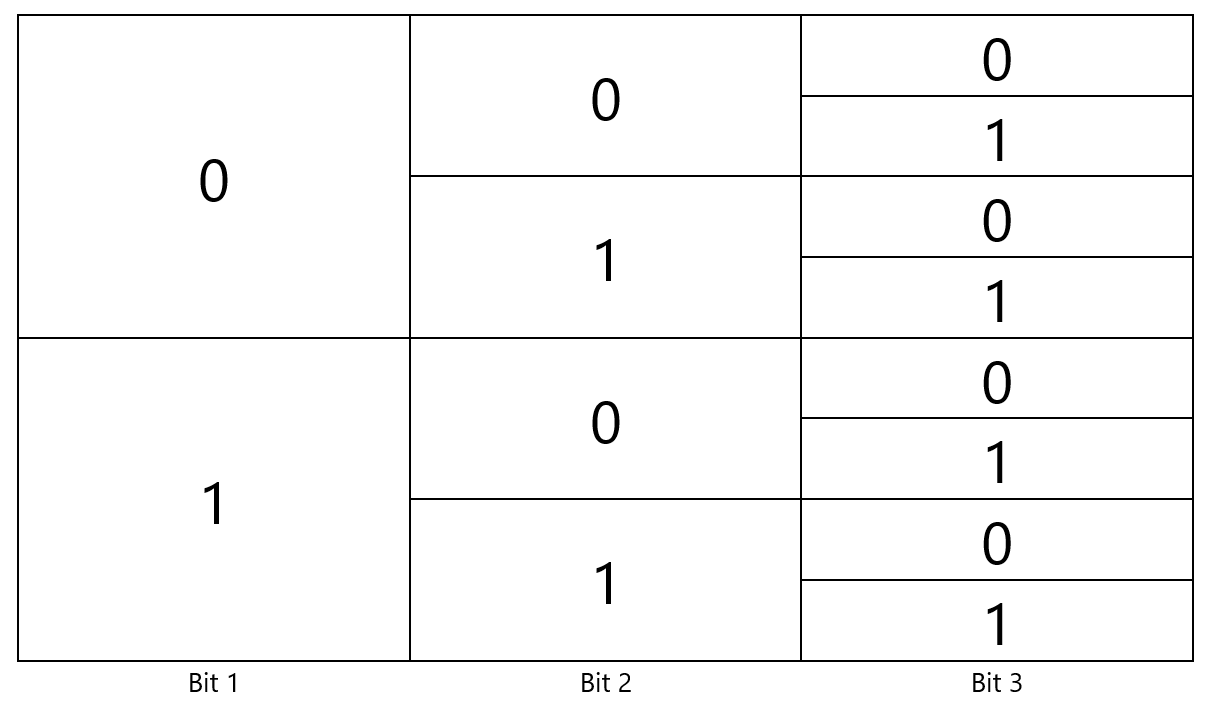
Để lựa chọn bit biểu diễn cho một codeword, ta đi từ trái qua phải, lấy số lượng bits cần thiết để biểu diễn cho một codeword. Ví dụ như 1 bit thì có thể sử dụng 0 hoặc 1, 2 bits thì có 00, 01, 10, 11. Và để đảm bảo không có codeword nào là tiền tố của codeword khác, khi gán một codeword, thực hiện loại bỏ các cột cùng dòng với bit cuối cùng của codeword đó khỏi bảng

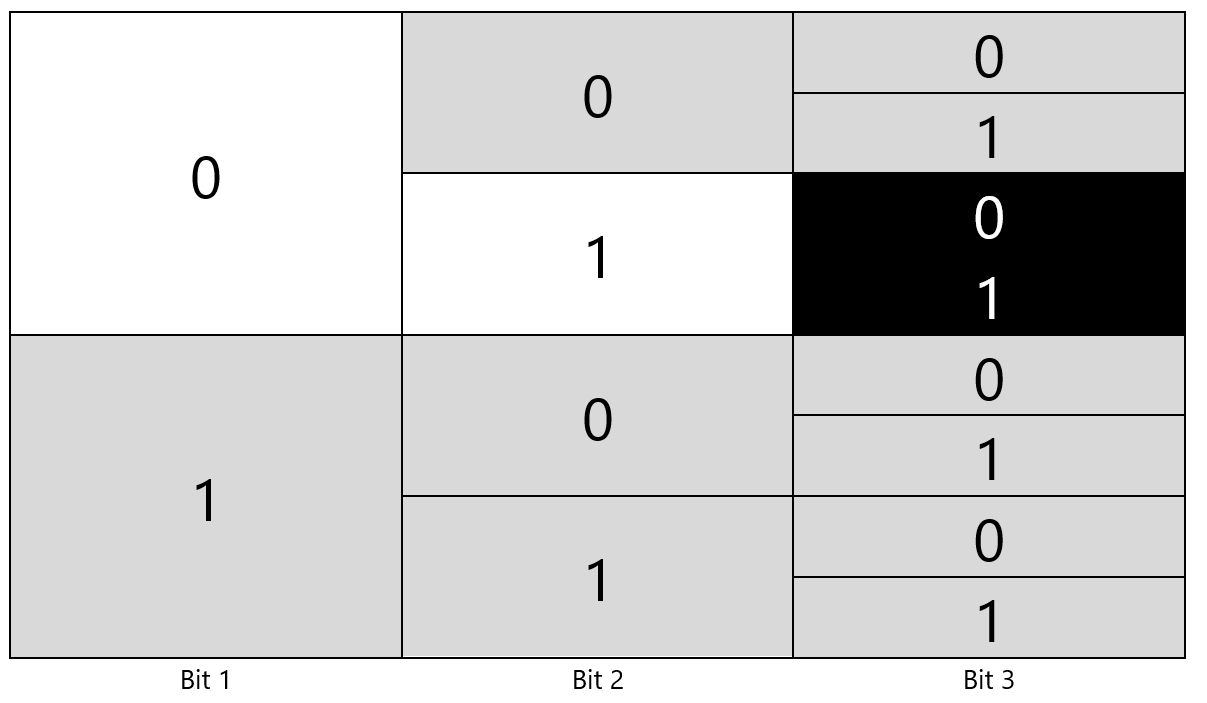
Ví dụ gán 01 cho một codeword thì phải bỏ hết 2 bits của cột thứ 3.

Dễ dàng nhận thấy rằng số lượng codeword có thể sử dụng (gọi là không gian codeword) là hữu hạn, tối đi 2 với 1 bit, 4 với 2 bits và 8 với 3 bits. Khi gán một bits biểu diễn cho một codeword, số phần từ của không gian codeword sẽ giảm đi tương ứng với số bit đã dùng. Ví dụ không gian codeword của một tổ hợp 3 bits tối đa là 8 ($2^3$). Tại sao lại là tối đa chứ không phải lúc nào cũng là 8? Nhìn vào bảng trên, nếu dùng 2 bit để biểu diễn cho một codeword, phải bỏ đi 2 phần tử trong không gian codeword, lúc này sẽ chỉ còn tối đa 7 codeword có thể được sử dụng. Tương tự như vậy nếu dùng 0 để biểu diễn, sẽ phải loại bỏ 4 phần tử. Dễ dàng nhận ra được quy luật: Do số hàng ở cột sau sẽ gấp đôi cột ở trước, một cách tổng quát, nếu lấy đang xét đến cột thứ $L$ và dùng $L$ bits này cho một codeword, sẽ phải loại bỏ $1/2^L$ phần tử khỏi không gian codeword. Ta có thể gọi đây là chi phí cho codeword có độ dài $L$. Chi phí cho codeword độ dài 1 là $1/2$, cho codeword độ dài 2 là $1/4$.

Ngược lại nếu biết chi phí cho một codeword $c = 1/2^L$ thì cóthể tính được độ dài bits biểu diễn codeword đó: $L = \log_2(1/c) = - \log_2(c)$

Quay trở lại với Alice và Bob. Do ký tự A xuất hiện với tần suất 50%, có thể sử dụng luôn $1/2$ không gian codeword cho A => số lượng bit để biểu diễn A là $-\log_2(0.5) = 1$, tương tự với B là $-\log_2(0.25) = 2$. Vậy nếu xác suất này không đẹp như thế thì sao? $P(X=A)=60\%$ chẳng hạn. Thì làm tròn thôi, $L_A=-log_2(0.6)=0.7369 \approx 1$.

Vậy khi biết tần suất xuất hiện của các ký tự trong bảng chữ cái, sẽ tính được số lượng bits tối thiểu để biểu diễn bảng chữ cái đó:

$$H = \sum_{x} p(x) \log_2 \left( \frac{1}{p(x)} \right) = -\sum_{x} p(x) \log_2(p(x)) \tag{3}$$

trong đó $x$ là ký tự trong bảng chữ cái, $p(x)$ là tần suất xuất hiện của $x$

$H$ còn được gọi là Entropy, và công thức (2) và (3) là giống nhau. Vậy Entropy còn có thể hiểu đơn giản như sau:

Entropy của một tín hiệu có phân phối $p$ là số lượng bits tối thiểu cần thiết để biễu diễn tín hiệu.

Thế thì nó liên quan gì đến mức độ hỗn loạn của tín hiệu? Vậy một tín hiệu hỗn loạn là như nào? Nó phụ thuộc vào số lượng ký tự trong bảng chữ cái hay hiểu rộng hơn là không gian sự kiện, và sự không chắc chắn của các sự kiện này. Nếu không gian chỉ có 1 sự kiện thì chắc chán nó sẽ xảy ra và không cần bit nào để mô tả nó. Nếu có 2 sự kiện nhưng 1 trong 2 chắc chắn xảy ra, cái còn lại thì không thì cũng không cần bit nào. Nhưng cũng với 2 sự kiện, không chắc chắn sự kiện nào sẽ xảy ra, xác xuất của mỗi sự kiện là $50\%$ thì cần 2 bit để biểu diễn mỗi sự kiện (có thể thấy số bit đã tăng lên cùng với sự không chắc chắn hay hỗn loạn của tín hiệu).

2.2 Cross Entropy

Quay trở lại với Alice và Bob. Khi cả 2 đều dùng bảng chữ cái có 4 ký tự A, B, C và D để nhắn tin, Alice đặc biệt thích dùng ký tự A với 50% xác suất xuất hiện. Do đó cả 2 đã quyết định mã hóa các ký tự bằng cách sử dụng:

0: A, 10: B, 110:C, 111:D

Bây giờ nếu Bob cũng sử dụng cách mã hóa trên nhưng có sự khác biệt về tần suất sử dụng các ký tự:

A: 25%, B: 25%, C: 25%, D: 25%

Gọi $p(x)$ và $q(x)$ là phân bố xác suất xuất hiện của ký tự trong bảng chữ cái của Alice và Bob. Lúc này số lượng bits trung bình mà Bob sử dụng là $E(X) = 0.25 * 1 + 0.25 * 2 + 0.25 * 3 * 2 = 2.25$

Đây chình là một ví dụ của Cross-Entropy. Giả sử mã hóa thông tin có phân phối $p(x)$ sử dụng bộ codeword tối ưu cho thông tin có phân phối $q(x)$ thì số lượng bit trung bình cần thiết là :

$$H ( p, q ) = H _ { q } ( p ) = \sum _ { x } p ( x ) \log ( \frac { 1 } { q ( x ) } ) = - \sum _ { x } p ( x ) \log ( q ( x ) ) \tag{4}$$

Đây chính là Entropy của tín hiệu $p(x)$ được mã hóa dựa vào phân phối $q(x)$ nên được gọi là Cross-Entropy hay Entropy chéo giữa 2 phân phối.

Tính chất của Cross-Entropy:

• Cross-Entropy luôn lớn hơn Entropy: $H(p,q) \geq H(q)$
• Cross-Entropy nhỏ nhất khi $p=q$
• Cross-Entropy không đối xứng: $H(p, q) \ne H(q, p)$

II. Cross-Entropy trong Machine Learning

Nhìn lại công thức (1) và (4) đã có sự tương đồng. Cross-Entropy trong học máy biễu diễn số lượng bits cần dùng để mã hóa phân phối của nhãn dùng phân phối dự đoán của mô hình. Số lượng bits càng nhỏ, dự đoán càng chính xác. Như vậy việc tối ưu các mô hình học máy sử dụng hàm cross-entropy loss là đang tối ưu các tham số để sự sai khác giữa phân phối của dự đoán và của thực tế là nhỏ nhất

Do xuất phát từ việc định lượng sự khác nhau giữa 2 phân phối, Cross-Entropy có những tính chất sau khiến nó được sử dụng nhiều trong các bài toán học máy, đặc biệt là lớp bài toán phân loại:

1. Hiệu quả với các mô hình xác suất: Cross-entropy đo lường sự khác biệt giữa hai phân phối xác suất: phân phối xác suất dự đoán bởi mô hình và phân phối xác suất thực tế của các nhãn. Trong các bài toán phân loại, mô hình học sâu thường đưa ra dự đoán dưới dạng xác suất, và cross-entropy là cách hiệu quả để đo lường mức độ "sai lệch" của những dự đoán này so với thực tế.
2. Nhạy cảm với sự thay đổi: với việc sử dụng logarit, Với 2 xác suất $p_i \ne q_i$ càng nhiều thì giá trị của Cross-Entropy càng lớn
3. Sự đơn giản: Cross-entropy có thể được tính toán một cách hiệu quả và không yêu cầu phép tính phức tạp. Điều này làm cho việc cập nhật trọng số trong quá trình huấn luyện mô hình học sâu trở nên dễ dàng và nhanh chóng.
4. Khi kết hợp với hàm softmax ở đầu ra của mô hình, Cross-Entropy cho ra một hàm có đạo hàm rất trơn (smooth) và ổn định, làm cho gradient không tăng quá lớn hay giảm quá nhỏ giúp giảm tình trạng "Vanishing Gradient" và "Exploding Gradient" (tham khảo thêm tại đây và đây)

Bonus

Có một điều thú vị là để đo sự khác nhau giữa hai phân phối, có thể sử dụng KL-Divergence:

$$D _ { k L } \left ( p \| q \right ) = \sum _ { x \in X } p \left ( x \right ) \log \left ( \frac { p \left ( x \right ) } { q \left ( x \right ) } \right ) = \sum _ { x \in X } p(x) \log p(x) - p(x) \log q(x) = H(p, q) - H(p)$$

KL-Divergence là hiệu của Cross-Entropy khi sử dụng $q$ để mã hóa $p$và Entropy của $p$

Trong các bài toán phân loại, Entropy của nhãn $H(P)$ là một hằng số đối với một bộ dữ liệu xác định. Do đó việc cực tiểu cross-entropy loss cũng tương đương với việc cực tiểu KL-Divergence.