1. Hồi quy tuyến tính (Linear Regression)

Thuật toán này dùng để xử lý các dữ liệu được phân bố theo dạng đường thẳng hoặc "gần thẳng" trên đồ thị. Hay nói ngắn gọn là dữ liệu có tính chất tuyến tính.

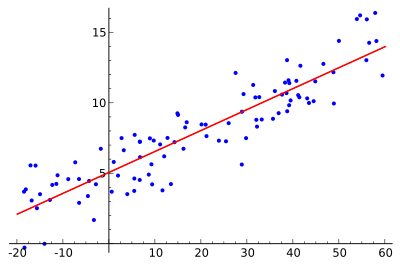
Ảnh minh hoạ các dữ liệu phân bố "trông" có vẻ là theo 1 đường thẳng.

Công thức

Tổng quát

$$\hat{y} = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n$$

• Với $x_{n}$ là các thuộc tính đầu vào
• $\hat{y}$ là kết quả đầu ra
• $\theta_n$ là các hệ số

Mục đích của quá trình huấn luyện là tìm ra các giá trị $\theta$ sao cho mô hình dự đoán kết quả sát nhất với dữ liệu thực tế.

Công thức trên có thể viết lại dưới dạng tổng quát dựa theo phép nhân ma trận như sau:

$$\hat{y} = \boldsymbol{\theta}^\intercal \boldsymbol{x}$$

• $x$ là vector đầu vào ($[x_1, x_2, ... x_n]$)
• ${\theta}^\intercal$ : Là phép chuyển vị của vector 𝜃
• $\hat{y}$ là vector chứa các kết quả dự đoán

Cần có 1 thông số nhằm đánh giá, đo lường kết quả của huấn luyện đã tối ưu chưa. Thông số đó là hàm mất mát (cost function).

$$\text{MSE}(X, h_\theta) = \frac{1}{m} \sum_{i=1}^{m} (\theta^\top x^{(i)} - y^{(i)})^2$$

• $(\theta^\top x^{(i)} - y^{(i)})$ là sai số của dự đoán so với thực tế.

MSE càng bé thì kết quả dự đoán của mô hình càng tốt. Quy lại sẽ phải tìm $\theta$ sao cho giá trị hàm mất mát nhỏ nhất.

The Normal Equation (Tìm θ)

Bài toán đặt ra ở trên là tìm θ để cho hàm mất mát MSE đạt giá trị nhỏ nhất. Bắt đầu từng bước một

• Bước 1: Tạo các dữ liệu theo 1 đường thẳng (có thêm nhiễu)

import numpy as np

np.random.seed(42)
m = 100  # 100 dữ liệu
X = 2 * np.random.rand(m, 1)  # Ngẫu nhiên 1 ma trận 100 hàng 1 cột
y = 4 + 3 * X + np.random.randn(m, 1)  # y = 4 + 3 * X + noise (nhiễu)

• Bước 2: Vẽ các điểm vừa tạo lên đồ thị

import matplotlib.pyplot as plt

plt.figure(figsize=(6, 4))
plt.plot(X, y, "b.")
plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.axis([0, 2, 0, 15])
plt.grid()
plt.show()

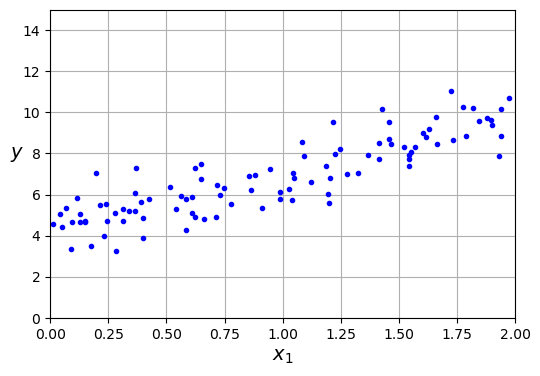
• Bước 3: Tìm θ tối ưu

Ta có công thức:

$\theta = \left(X^\top X\right)^{-1} X^\top y$

from sklearn.preprocessing import add_dummy_feature

X_b = add_dummy_feature(X)  # cài đặt x0 = 1 với tất cả dữ liệu
# Tính theta tối ưu
theta_best = np.linalg.inv(X_b.T @ X_b) @ X_b.T @ y

print(theta_best)

"""
array([[4.21509616],
           [2.77011339]])

y = 4.21 + 2.77 * x
"""

LinearRegression thực chất dùng một công thức khác thay vì công thức tính θ ở trên. Thay vì ma trận nghịch đảo thì sẽ dùng ma trận giả nghịch đảo (pseudoinverse) .

$$\theta = X^+ y$$

Cách sử dụng ma trận giả nghịch đảo tối ưu hơn, với một số lý do sau

• Không phải lúc nào $X^{T}X$ cũng khả nghịch
• Tính ma trận nghịch đảo với các ma trận lớn rất tốn kém tài nguyên

# pinv là hàm lấy nghịch đảo giả của ma trận
np.linalg.pinv(X_b) @ y

"""
array([[4.21509616],
           [2.77011339]])
"""

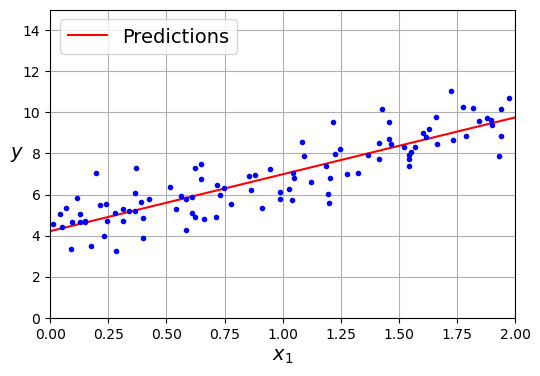
• Bước 4: Biểu diễn đường thẳng mà mô hình cho ra lên đồ thị

import matplotlib.pyplot as plt

plt.figure(figsize=(6, 4))
plt.plot(X_new, y_predict, "r-", label="Predictions")
plt.plot(X, y, "b.")

plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.axis([0, 2, 0, 15])
plt.grid()
plt.legend(loc="upper left")

plt.show()

2. Gradient Descent

Trong thực tế với các bộ dữ liệu lớn, nhiều thuộc tính. Việc tính trực tiếp ra giá trị của $\theta$ như phần trên sẽ mất rất nhiều thời gian.

• Độ phức tạp của công thức sử dụng ma trận nghịch đảo: $O(n^3)$
• Độ phức tạp của công thức sử dụng ma trận giả nghịch đảo: $O(n^2)$

Gradient Descent là một cách tiếp cận khác để tính toán $\theta$. Ý tưởng cơ bản của phương pháp này là chọn ngẫu nhiên một $\theta$ ban đầu, sau đó lặp lại nhiều lần cho đến khi tìm được vị trí nơi hàm mất mát nhỏ nhất.

Learning Rate dịch nôm na là tốc độ học. Nếu thông số này quá bé thì mô hình sẽ mất nhiều thời gian đạt tới giá trị mong muốn. Ngược lại, nếu quá lớn thì mô hình có thể bị "lạc" và không tìm được giá trị bé nhất.

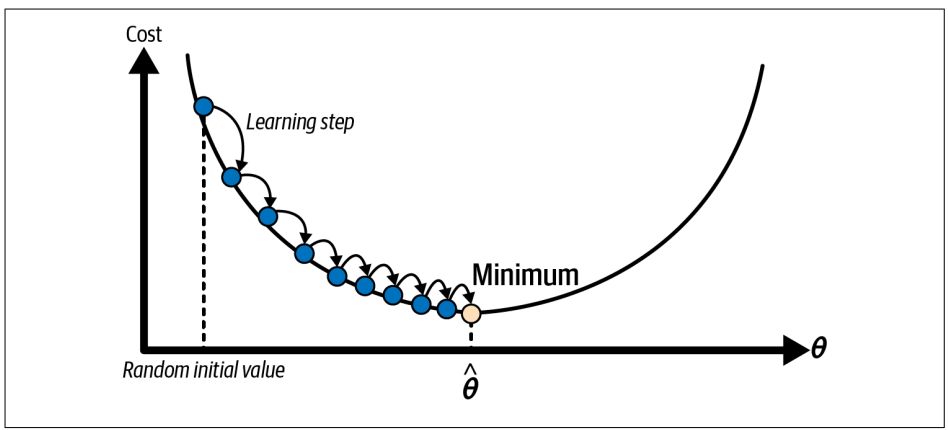
• Gradient Descent tối ưu bằng cách nhảy cóc dần đến giá trị nhỏ nhất.

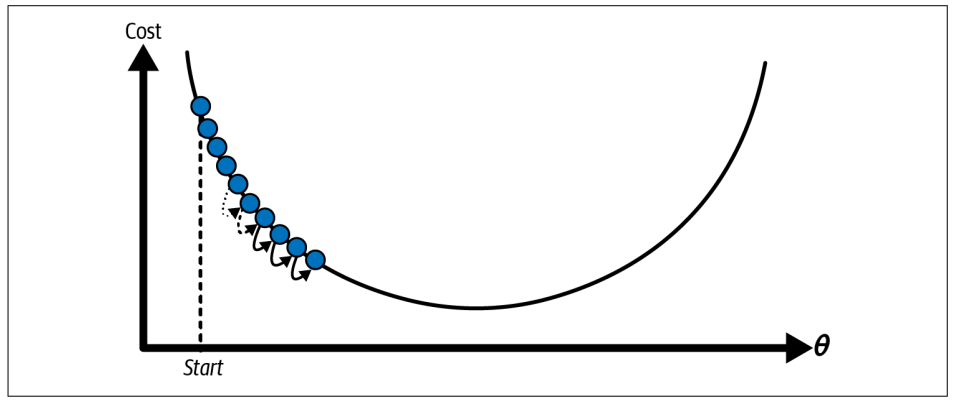
• Trường hợp Learning Rate quá bé => tốn nhiều bước và thời gian để đạt đến giá trị tối ưu

Trường hợp Learning Rate quá lớn => giao động quanh giá trị bé nhất chứ không đạt đến.

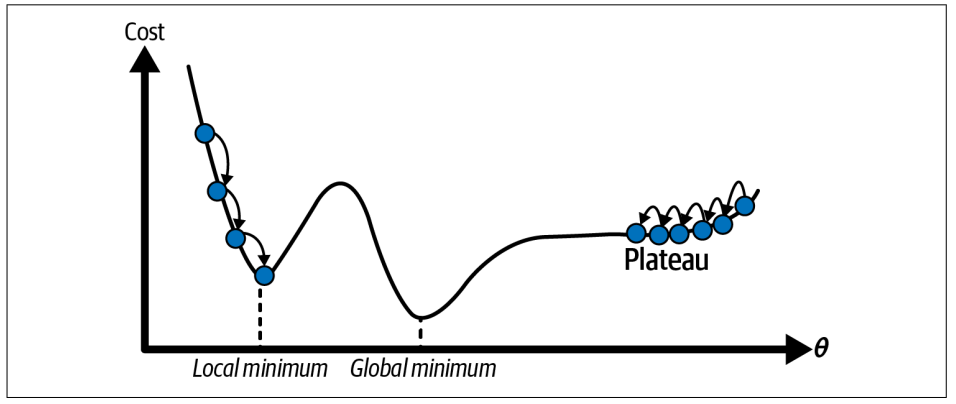
• Nếu khởi tạo ngẫu nhiên ở bên trái hình vẽ, thuật toán rơi vào local minimum → không tìm được nghiệm tốt nhất.
• Nếu khởi tạo ở bên phải, thuật toán sẽ phải rất lâu mới “bò” được qua vùng phẳng

Tuy nhiên, với mô hình hồi quy tuyến tính thì chúng ta sẽ không gặp phải vấn đề trên (Do không có local minimum và đồ thị hàm mất mát cũng đẹp).

Batch Gradient Descent

• Mục tiêu của Gradient descent là giảm dần giá trị của hàm mất mát (cost function).
• Để làm được điều trên, ta cần biết phải thay đổi các tham số θ như thế nào để làm giảm giá trị của hàm mất mát.

Ta sẽ dùng đến khái niệm đạo hàm riêng (partial derivative).

Đạo hàm riêng: Cho biết tốc độ thay đổi của hàm theo một biến cụ thể, trong khi các biến khác được giữ nguyên.

Công thức tính đạo hàm riêng của hàm mất mát MSE:

$$\frac{\partial}{\partial \theta_j} \text{MSE}(\theta) = \frac{2}{m} \sum_{i=1}^{m} \left(\theta^\top x^{(i)} - y^{(i)}\right) x_j^{(i)}$$

Đạo hàm riêng cho biết, khi thay đổi $\theta_j$ (các tham số khác giữ nguyên) thì hàm mất mát thay đổi nhanh hay chậm, tăng hay giảm.

• Nếu đạo hàm riêng > 0: Tăng $\theta_j$ sẽ tăng giá trị MSE => Cần giảm $\theta_j$ để đến gần hơn cực tiểu
• Nếu đạo hàm riêng < 0: Tăng $\theta_j$ đồng thời sẽ giảm MSE => Tăng $\theta_j$

=> Đạo hàm riêng ngược hướng với $\theta_j$

Tổng hợp toàn bộ các giá trị đạo hàm riêng của từng thuộc tính, ta có:

$$\nabla_\theta \text{MSE}(\theta) = \begin{bmatrix} \frac{\partial}{\partial \theta_0} \text{MSE}(\theta) \\ \frac{\partial}{\partial \theta_1} \text{MSE}(\theta) \\ \vdots \\ \frac{\partial}{\partial \theta_n} \text{MSE}(\theta) \end{bmatrix} = \frac{2}{m} X^\top (X\theta - y)$$

Vì gradient $\nabla_\theta \text{MSE}(\theta)$ ngược hướng với $\theta$, ta có:

$\theta_{\text{next step}} = \theta - \eta \nabla_\theta \text{MSE}(\theta)$ Với $\eta$ là learning rate

eta = 0.1  # learning rate
n_epochs = 1000
m = len(X_b)

np.random.seed(42)
theta = np.random.randn(2, 1)  # Chọn ngẫu nhiên theta ban đầu

for epoch in range(n_epochs):
    gradients = 2 / m * X_b.T @ (X_b @ theta - y)
    theta = theta - eta * gradients # cập nhật lại theta

• In ra kết quả sau 1000 lần lặp

print(theta)
"""
    array([[4.21509616],
           [2.77011339]])
y = 4.21 + 2.77 * x
"""

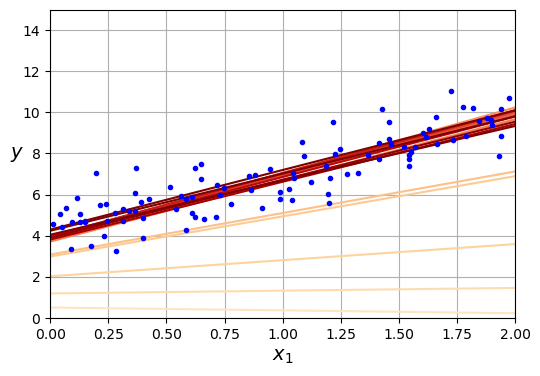
• Vẽ đồ thị mô tả quá trình gradient descent với các learning rate khác nhau

import matplotlib as mpl

def plot_gradient_descent(theta, eta):
    m = len(X_b)
    plt.plot(X, y, "b.")
    n_epochs = 1000
    n_shown = 20
    theta_path = []
    for epoch in range(n_epochs):
        if epoch < n_shown:
            y_predict = X_new_b @ theta
            color = mpl.colors.rgb2hex(plt.cm.OrRd(epoch / n_shown + 0.15))
            plt.plot(X_new, y_predict, linestyle="solid", color=color)
        gradients = 2 / m * X_b.T @ (X_b @ theta - y)
        theta = theta - eta * gradients
        theta_path.append(theta)
    plt.xlabel("$x_1$")
    plt.axis([0, 2, 0, 15])
    plt.grid()
    plt.title(fr"$\eta = {eta}$")
    return theta_path

np.random.seed(42)
theta = np.random.randn(2, 1)

plt.figure(figsize=(10, 4))
plt.subplot(131)
plot_gradient_descent(theta, eta=0.02)
plt.ylabel("$y$", rotation=0)
plt.subplot(132)
theta_path_bgd = plot_gradient_descent(theta, eta=0.1)
plt.gca().axes.yaxis.set_ticklabels([])
plt.subplot(133)
plt.gca().axes.yaxis.set_ticklabels([])
plot_gradient_descent(theta, eta=0.5)
plt.show()

Minh hoạ cho 3 trường hợp learning rate quá nhỏ, quá to và vừa đã đề cập ở trên.

Stochastic Gradient Descent

Batch gradient descent sử dụng toàn bộ dữ liệu huấn luyện trong quá trình tính toán, đặt ra vấn đề hiệu năng, tốc độ xử lý với một tập dữ liệu lớn.

Stochastic Gradient Descent sẽ chọn ngẫu nhiên mỗi dữ liệu ở từng bước tính toán thay vì toàn bộ dữ liệu huấn luyện. Điều này giúp tăng tốc độ thuật toán lên nhiều lần !

theta_path_sgd = []
n_epochs = 50  # Số lần lặp qua toàn bộ dữ liệu
t0, t1 = 5, 50  # Các tham số điều chỉnh tốc độ học (learning schedule)

# Hàm điều chỉnh tốc độ học, giảm dần theo số bước lặp
def learning_schedule(t):
    return t0 / (t + t1)

np.random.seed(42)
theta = np.random.randn(2, 1)  # Khởi tạo ngẫu nhiên tham số theta ban đầu

n_shown = 20  # Số lần hiển thị dự đoán trên đồ thị
plt.figure(figsize=(6, 4))

for epoch in range(n_epochs):
    # Lặp qua từng mẫu dữ liệu
    for iteration in range(m):
        # Hiển thị dự đoán trong epoch đầu tiên (chỉ để minh họa)
        if epoch == 0 and iteration < n_shown:
            y_predict = X_new_b @ theta  # Dự đoán giá trị y
            color = mpl.colors.rgb2hex(plt.cm.OrRd(iteration / n_shown + 0.15))  # Màu sắc cho từng lần lặp
            plt.plot(X_new, y_predict, color=color)  # Vẽ đường dự đoán

        # Chọn ngẫu nhiên một mẫu dữ liệu
        random_index = np.random.randint(m)
        xi = X_b[random_index : random_index + 1]  # Lấy một hàng dữ liệu X
        yi = y[random_index : random_index + 1]  # Lấy nhãn tương ứng

        # Tính gradient (không chia cho m như trong Batch Gradient Descent)
        gradients = 2 * xi.T @ (xi @ theta - yi)
        eta = learning_schedule(epoch * m + iteration)  # Tính tốc độ học
        theta = theta - eta * gradients  # Cập nhật tham số theta
        theta_path_sgd.append(theta)  # Lưu lại giá trị theta

# Vẽ các điểm dữ liệu và hiển thị đồ thị
plt.plot(X, y, "b.")  # Vẽ các điểm dữ liệu thực tế
plt.xlabel("$x_1$")  # Nhãn trục x
plt.ylabel("$y$", rotation=0)  # Nhãn trục y
plt.axis([0, 2, 0, 15])  # Giới hạn trục
plt.grid()  # Hiển thị lưới
plt.show()  # Hiển thị đồ thị

• Sau nhiều lần lặp thì đường thẳng đã khá "khớp" với dữ liệu !

• In ra kết quả

print(theta)
"""
array([[4.21076011],
       [2.74856079]])
"""

Lưu ý: SGD vẫn đảm bảo độ chính xác tương đương BGD trong thực tế !

Mini-batch gradient descent

Mini-batch gradient descent đúng như tên gọi của nó, là thuật toán phiên bản nhỏ hơn của BGD. Ở mỗi bước sẽ lấy ngẫu nhiên một nhóm nhỏ từ dữ liệu huấn luyện thay vì cả tập hay chỉ 1 dữ liệu như SGD.

from math import ceil

n_epochs = 50
minibatch_size = 20 # Kích thước mỗi minibatch
n_batches_per_epoch = ceil(m / minibatch_size)

np.random.seed(42)
theta = np.random.randn(2, 1)

t0, t1 = 200, 1000

def learning_schedule(t):
    return t0 / (t + t1)

theta_path_mgd = []
for epoch in range(n_epochs):
    shuffled_indices = np.random.permutation(m)
    X_b_shuffled = X_b[shuffled_indices]
    y_shuffled = y[shuffled_indices]
    for iteration in range(0, n_batches_per_epoch):
        idx = iteration * minibatch_size
        xi = X_b_shuffled[idx : idx + minibatch_size]
        yi = y_shuffled[idx : idx + minibatch_size]
        gradients = 2 / minibatch_size * xi.T @ (xi @ theta - yi)
        eta = learning_schedule(iteration)
        theta = theta - eta * gradients
        theta_path_mgd.append(theta)

theta_path_bgd = np.array(theta_path_bgd)
theta_path_sgd = np.array(theta_path_sgd)
theta_path_mgd = np.array(theta_path_mgd)

plt.figure(figsize=(7, 4))
plt.plot(theta_path_sgd[:, 0], theta_path_sgd[:, 1], "r-s", linewidth=1,
         label="Stochastic")
plt.plot(theta_path_mgd[:, 0], theta_path_mgd[:, 1], "g-+", linewidth=2,
         label="Mini-batch")
plt.plot(theta_path_bgd[:, 0], theta_path_bgd[:, 1], "b-o", linewidth=3,
         label="Batch")
plt.legend(loc="upper left")
plt.xlabel(r"$\theta_0$")
plt.ylabel(r"$\theta_1$   ", rotation=0)
plt.axis([2.6, 4.6, 2.3, 3.4])
plt.grid()
plt.show()

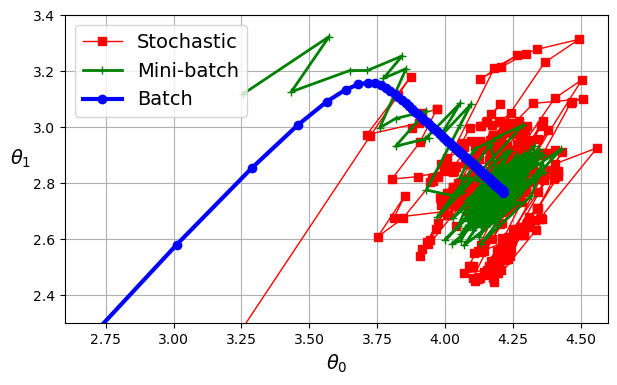
Từ hình trên, ta thấy rằng:

• Batch GD: đi thẳng, ổn định đến điểm cực tiểu và dừng hẳn.
• SGD: rung lắc, dao động quanh cực tiểu.
• Mini-batch GD: dao động nhẹ hơn SGD, gần hơn với cực tiểu, nhưng không ổn định như Batch GD.

Tài liệu tham khảo

https://github.com/ageron/handson-ml3/blob/main/04_training_linear_models.ipynb