1. Cài đặt môi trường

Bước 1. Cài đặt Anacoda và các thư viện liên quan

# Linux x86
curl -O https://repo.anaconda.com/archive/Anaconda3-2024.10-1-Linux-x86_64.sh

chmod +x Anaconda3-2024.10-1-Linux-x86_64.sh
./Anaconda3-2024.10-1-Linux-x86_64.sh

conda init [bash/zsh/fish]

# Cài python
conda create -n myenv python=3.12

# Cài thư viện
conda activate myenv
conda install pandas matplotlib scikit-learn numpy

Bước 2. Kiểm tra phiên bản

Yêu cầu Python 3.7 trở lên:

import sys

assert sys.version_info >= (3, 7)

Yêu cầu Scikit-Learn ≥ 1.0.1:

from packaging import version
import sklearn

assert version.parse(sklearn.__version__) >= version.parse("1.0.1")

Bước 3. Cấu hình cho matplotlib

import matplotlib.pyplot as plt

plt.rc('font', size=14)
plt.rc('axes', labelsize=14, titlesize=14)
plt.rc('legend', fontsize=14)
plt.rc('xtick', labelsize=10)
plt.rc('ytick', labelsize=10)

Lưu ý Nếu vẽ biểu đồ gặp lỗi: Could not find the Qt platform plugin 'wayland' thì chạy lệnh sau trên Linux.

sudo apt install qtwayland5

2. MNIST

MNIST (Modified National Institute of Standards and Technology) là một tập dữ liệu phổ biến được sử dụng để thử nghiệm các mô hình nhận dạng chữ số viết tay.

• Tải về bộ dữ liệu

# Tải mnist
from sklearn.datasets import fetch_openml

mnist = fetch_openml('mnist_784', as_frame=False)

• Xem qua các thông số và thuộc tính của bộ dữ liệu

mnist.keys()  # Các thuộc tính trong bộ dữ liệu. Ở đây chúng ta sẽ chỉ dùng `data` và `target`
# dict_keys(['data', 'target', 'frame', 'categories', 'feature_names', 'target_names', 'DESCR', 'details', 'url'])

# X là dữ liệu, y là nhãn dán của dữ liệu
X, y = mnist.data, mnist.target
X

"""
  array([[0, 0, 0, ..., 0, 0, 0],
           [0, 0, 0, ..., 0, 0, 0],
           [0, 0, 0, ..., 0, 0, 0],
           ...,
           [0, 0, 0, ..., 0, 0, 0],
           [0, 0, 0, ..., 0, 0, 0],
           [0, 0, 0, ..., 0, 0, 0]], shape=(70000, 784))
"""

# Có 70.000 mẫu dữ liệu chữ viết tay, kích thước 28 x 28 pixels = 784
X.shape # (70000, 784)

# Nhãn của dữ liệu
y # array(['5', '0', '4', ..., '4', '5', '6'], dtype=object)

• Vẽ ảnh từ dữ liệu pixel

# Vẽ ảnh từ dữ liệu pixel
import matplotlib.pyplot as plt

def plot_digit(image_data):
    image = image_data.reshape(28, 28)
    plt.imshow(image, cmap="binary")
    plt.axis("off")

some_digit = X[0]
plot_digit(some_digit)
plt.show()

# Ảnh trên có đáp án là 5
y[0] # '5'

• Xem thử 100 dữ liệu đầu tiên hình thù như thế nào

# 
plt.figure(figsize=(9, 9))
for idx, image_data in enumerate(X[:100]):
    plt.subplot(10, 10, idx + 1)
    plot_digit(image_data)
plt.subplots_adjust(wspace=0, hspace=0)
plt.show()

• Chia tập huấn luyện và tập kiểm thử theo tỷ lệ 6 / 1

X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]

3. Phân loại nhị phân (Training a Binary Classifier)

Trước tiên chúng ta thử phân loại xem một dữ liệu là 5 hay khác 5 trước.

• Lấy tất cả nhãn có giá trị bằng 5

y_train_5 = (y_train == '5')
y_test_5 = (y_test == '5')

• Huấn luyện mô hình

# Dùng thuật toán SGDClassifier có sẵn trong sklearn. Tạm thời chưa cần quan tâm chi tiết
from sklearn.linear_model import SGDClassifier

sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train_5)

• Dùng mô hình dự đoán thử

# Dự đoán:
# - Trả về True nếu dự đoán là 5
# - Trả về False nếu dự đoán là khác 5
sgd_clf.predict([X[0]]) # array([ True])

4. Đánh giá hiệu năng mô hình

Đánh giá độ chính xác với Cross-Validation

Cross-validation (CV) là một kỹ thuật chia dữ liệu huấn luyện thành nhiều phần và huấn luyện luân phiên trên các phần đó.

• Mỗi phần được gọi là fold
• Mỗi chu kỳ huấn luyện sẽ "giấu" đi một phần dữ liệu, tránh việc học tủ của mô hình và đem phần đó ra kiểm tra.

from sklearn.model_selection import cross_val_score

# Chia làm 3 folds
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")

• Đo độ chính xác bằng cách chạy vòng lặp tính (số dự đoán đúng) / (tổng số dự đoán)

from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone

skfolds = StratifiedKFold(n_splits=3)

for train_index, test_index in skfolds.split(X_train, y_train_5):
    clone_clf = clone(sgd_clf)
    X_train_folds = X_train[train_index]
    y_train_folds = y_train_5[train_index]
    X_test_fold = X_train[test_index]
    y_test_fold = y_train_5[test_index]

    clone_clf.fit(X_train_folds, y_train_folds)
    y_pred = clone_clf.predict(X_test_fold)
    n_correct = sum(y_pred == y_test_fold)
    # In ra độ chính xác trên từng fold
    print(n_correct / len(y_pred))
    
 # Kết quả in ra
""" 
0.95035
0.96035
0.9604
"""

Độ chính xác khá cao, nhưng cần kiểm tra lại phân bố dữ liệu xem có cân bằng không bằng DummyClassifier

DummyClassifier dự đoán theo một ý tưởng rất đơn giản là luôn đoán nhãn phổ biến nhất.

from sklearn.dummy import DummyClassifier

dummy_clf = DummyClassifier()
dummy_clf.fit(X_train, y_train_5)
print(any(dummy_clf.predict(X_train)))

• Xem độ chính xác của DummyClassifier

cross_val_score(dummy_clf, X_train, y_train_5, cv=3, scoring="accuracy")

# Kết quả: array([0.90965, 0.90965, 0.90965])

Tỷ lệ chính xác ở ngưỡng 90% => Chứng tỏ đang đang có sự thiên lệch và phân bố dữ liệu với tỷ lệ 9 / 1 khi số dữ liệu có nhãn là 5 nhiều gấp 9 lần các số còn lại.

Confusion Matrix

Confusion matrix tạm dịch là ma trận nhầm lẫn thể hiện chi tiết số lượng dự đoán sai và dự đoán sai như thế nào ?

Một Confusion matrix sẽ có dạng

Nhãn	Dự đoán Negative (N)	Dự đoán Positive (P)
Negative	True Negative (TN)	False Positive (FP)
Positive	False Negative (FN)	True Positive (TP)

• Ảnh là số 5 là Positive
• Ảnh số khác 5 là Negative

• TN: Nhãn Native và cũng được dự đoán là Negative => Đúng (True Negative)
• FN: Nhãn Positve nhưng dự đoán là Negative => Sai (False Negative)
• FP: Nhãn Positive nhưng dự đoán là Negative => Sai (False Positive)
• TP: Nhãn Positive và cũng được dự đoán là Positive => Đúng (True Positive)

Tóm lại: Kết quả dự đoán + nhãn dự đoán => (TN/FN/FP/TP)

• Cho mô hình dự đoán

from sklearn.model_selection import cross_val_predict

y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)

• Tính confusion_matrix

from sklearn.metrics import confusion_matrix

cm = confusion_matrix(y_train_5, y_train_pred)
print(cm) 

"""
array([[53892,   687],
           [ 1891,  3530]])
"""

Từ ma trận ta có bảng sau:

Thực tế \ Dự đoán	Không phải số 5	Là số 5
Không phải số 5	53,892 (TN)	687 (FP)
Là số 5	1,891 (FN)	3,530 (TP)

Precision and Recall (Độ chuẩn xác và độ nhạy)

Từ Confusion Matrix ở trên, ta có thể tính hai thông số quan trọng là Precision và Recall

Precision

$$\text{Precision} = \frac{TP}{FP + TP}$$

• Precision Cao => FP thấp: Mô hình ít dự đoán sai Positive.
• Precision Thấp => FP cao: Mô hình dự đoán nhiều Positive sai.

Với Positive là trường hợp bị bệnh, tiến hành dự đoán một người có bị bệnh không. Precision cao có nghĩa ít người khỏe bị chẩn đoán mắc bệnh.

# Tính precision bằng hàm của sklearn
from sklearn.metrics import precision_score

precision_score(y_train_5, y_train_pred)  # == 3530 / (687 + 3530) = 0.837 (83.7%) 

# Kết quả: 0.8370879772350012

• Hoặc tính thủ công

# tính thủ công
cm[1, 1] / (cm[0, 1] + cm[1, 1]) #  np.float64(0.8370879772350012)

Recall

$$\text{Recall} = \frac{TP}{TP + FN}$$

• Recall Cao => FN thấp: Mô hình đoán được phần lớn các trường hợp Positive.
• Recall Thấp => FN cao: Mô hình bỏ sót nhiều Positive (nhiều FN).

Recall cao có nghĩa là ít bệnh nhân bị bỏ sót.

Lưu ý: Precision và Recall thường tỷ lệ nghịch

from sklearn.metrics import recall_score
# Tính recall
recall_score(y_train_5, y_train_pred)  # == 3530 / (1891 + 3530) = 0.651 (65.1%)

# Kết quả: 0.6511713705958311

• Hay

# TP / (FN + TP)
cm[1, 1] / (cm[1, 0] + cm[1, 1]) # np.float64(0.6511713705958311)

F1 Score

F1 score là chỉ số kết hợp giữa precision và recall. Được tính theo công thức sau:

from sklearn.metrics import f1_score

f1_score(y_train_5, y_train_pred) #  0.7325171197343847

• Hoặc tính thủ công

# Tính thủ công
cm[1, 1] / (cm[1, 1] + (cm[1, 0] + cm[0, 1]) / 2) # np.float64(0.7325171197343847)

Trong F1 score, độ chính xác (precision) và độ nhạy (recall) tương đương nhau. Tuy nhiên, điều này không phải lúc nào cũng phù hợp với mục tiêu của mô hình: trong một số trường hợp, chúng ta quan tâm nhiều đến độ chính xác, trong khi ở những trường hợp khác, độ nhạy mới là yếu tố được ưu tiên hơn.

Ví dụ 1: Ứng dụng phân loại video an toàn dành cho trẻ em. Chúng ta sẽ ưu tiên việc các video an toàn được đề xuất đúng (precision cao) mặc dù điều đó có thể khiến nhiều video tốt bị loại bỏ (recall sẽ thấp).

Ví dụ 2: Phát hiện kẻ khả nghi qua hình ảnh giám sát. Độ chính xác có thể ở mức vừa phải chấp nhận được, nhưng độ nhạy recall cần cao để không để lọt một kẻ xấu nào.

Precision/Recall và sự đánh đổi

Như đã biết, Precision và Recall tỷ lệ nghịch với nhau nên muốn đạt được yếu tố này phải hy sinh thông số còn lại. Việc điều chỉnh tỷ lệ Precision/Recall của mô hình có thể dùng một thông số là threshold (ngưỡng).

• Hàm decision_function trả về giá trị độ tin cậy của dự đoán (càng lớn thì càng tin cậy)

y_scores = sgd_clf.decision_function([some_digit])
print(y_scores)

# Kết quả: array([2164.22030239])

• Ví dụ chọn threshold = 0, nếu y_scores > 0 thì dự đoán là 5

threshold = 0
y_some_digit_pred = (y_scores > threshold)

Làm sao để chọn thông số threshold cho phù hợp ? Chúng ta sẽ cùng vẽ đồ thị và xác định threshold mong muốn sao cho precision >= 90%

• Tính y_scores cho tất cả dữ liệu trong tập huấn luyện

y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3,
                             method="decision_function")

• Tính precision, recall với nhiều giá threshold khác nhau. Recall và precision min, max là các giá trị biên

from sklearn.metrics import precision_recall_curve

precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)

# 60k giá trị
print(len(precisions))
print(len(recalls))
print(len(thresholds))

"""
    60001
    60001
    60000
"""

• Vẽ đồ thị

plt.figure(figsize=(8, 4))
plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)
plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)
plt.vlines(threshold, 0, 1.0, "k", "dotted", label="threshold")

idx = (thresholds >= threshold).argmax()
plt.plot(thresholds[idx], precisions[idx], "bo")
plt.plot(thresholds[idx], recalls[idx], "go")
plt.axis([-50000, 50000, 0, 1])
plt.grid()
plt.xlabel("Threshold")
plt.legend(loc="center right")
plt.show()

import matplotlib.patches as patches

plt.figure(figsize=(6, 5))

plt.plot(recalls, precisions, linewidth=2, label="Precision/Recall curve")

plt.plot([recalls[idx], recalls[idx]], [0., precisions[idx]], "k:")
plt.plot([0.0, recalls[idx]], [precisions[idx], precisions[idx]], "k:")
plt.plot([recalls[idx]], [precisions[idx]], "ko",
         label="Point at threshold 3,000")
plt.gca().add_patch(patches.FancyArrowPatch(
    (0.79, 0.60), (0.61, 0.78),
    connectionstyle="arc3,rad=.2",
    arrowstyle="Simple, tail_width=1.5, head_width=8, head_length=10",
    color="#444444"))
plt.text(0.56, 0.62, "Higher\nthreshold", color="#333333")
plt.xlabel("Recall")
plt.ylabel("Precision")
plt.axis([0, 1, 0, 1])
plt.grid()
plt.legend(loc="lower left")

plt.show()

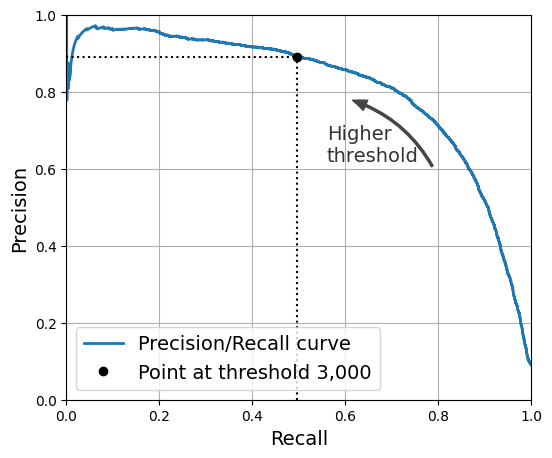
• Tìm giá trị threshold ứng với precisions >= 90%

idx_for_90_precision = (precisions >= 0.90).argmax()
threshold_for_90_precision = thresholds[idx_for_90_precision]
threshold_for_90_precision 

# Kết quả: np.float64(3370.0194991439557)

• Áp dụng threshold mới cho đầu ra

y_train_pred_90 = (y_scores >= threshold_for_90_precision)

• Tính lại precision và recall xem precision có đúng >= 90% hay không ?

precision_score(y_train_5, y_train_pred_90) # 0.9000345901072293


recall_at_90_precision = recall_score(y_train_5, y_train_pred_90)
recall_at_90_precision #  0.4799852425751706

The ROC Curve

ROC Curve là một công cụ khác để đánh giá mô hình phân loại nhị phân như Precision/Recall. Thay vì tính toán Precision và Recall thì ROC sẽ tính toán recall (true postitive rate - TPR) và fall-out (false postive rate - FPR) với:

$$FPR = \frac{FP}{TN + FP}$$

FPR có ý nghĩa đo lường tỷ lệ các mẫu âm tính bị dự đoán sai là dương tính.

Đường cong Precision/Recall sẽ nên được sử dụng trong các trường hợp lớp Positive hiếm hay mục đích bài toán quan tâm False Postive nhiều hơn False Nagative. Nếu không, nên dùng ROC.

• Tính toán các thông số của ROC với hàm roc_curve từ thư viện Sklear

from sklearn.metrics import roc_curve

fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)

• Vẽ đường cong ROC

idx_for_threshold_at_90 = (thresholds <= threshold_for_90_precision).argmax()
tpr_90, fpr_90 = tpr[idx_for_threshold_at_90], fpr[idx_for_threshold_at_90]

plt.figure(figsize=(6, 5))  # extra code – not needed, just formatting
plt.plot(fpr, tpr, linewidth=2, label="ROC curve")
plt.plot([0, 1], [0, 1], 'k:', label="Random classifier's ROC curve")
plt.plot([fpr_90], [tpr_90], "ko", label="Threshold for 90% precision")

plt.gca().add_patch(patches.FancyArrowPatch(
    (0.20, 0.89), (0.07, 0.70),
    connectionstyle="arc3,rad=.4",
    arrowstyle="Simple, tail_width=1.5, head_width=8, head_length=10",
    color="#444444"))
plt.text(0.12, 0.71, "Higher\nthreshold", color="#333333")
plt.xlabel('False Positive Rate (Fall-Out)')
plt.ylabel('True Positive Rate (Recall)')
plt.grid()
plt.axis([0, 1, 0, 1])
plt.legend(loc="lower right", fontsize=13)

plt.show()

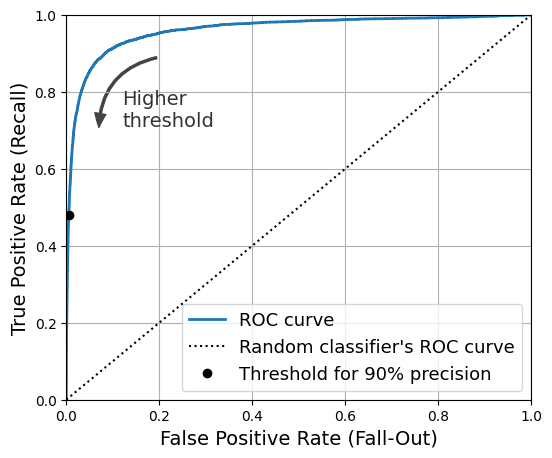
Thông số đánh giá hiệu suất của đường cong ROC gọi là AUC (Area Under the Curve) tạm dịch là diện tích dưới đường cong. AUC nằm trong khoảng [0, 1]

from sklearn.metrics import roc_auc_score

roc_auc_score(y_train_5, y_scores)

# Kết quả: np.float64(0.9604938554008616)

5. Phân loại nhiều lớp (Multiclass Classification)

Có 2 chiến lược cơ bản trong việc phân loại nhiều lớp:

• 1.one-versus-the-rest (OvR): Khi muốn phân loại một hình ảnh, tính toán xác xuất mà dữ liệu thuộc về các lớp, sau đó chọn lớp được cho điểm cao nhất. OvR đôi được gọi là one-versus-all (OvA).
• 2.one-versus-one (OvO): huấn luyện một bộ phân loại nhị phân theo từng cặp, cứ như vậy và sẽ chọn ra được lớp cuối cùng. Ví dụ có N lớp thì cần có N * (N - 1) / 2 cặp.

Đối với hầu hết các trường hợp, OvR được ưa chuộng hơn.

Chạy kiểu OvR

SVM làm việc không tốt với các tập dữ liệu lớn, nên ta chỉ huấn luyện trên 2000 mẫu đầu tiên, nếu không đoạn code dưới đây sẽ mất rất nhiều thời gian để chạy.

• Huấn luyện

from sklearn.svm import SVC

svm_clf = SVC(random_state=42)
svm_clf.fit(X_train[:2000], y_train[:2000])  # y_train, not y_train_5

• Sau khi huấn luyện, thử dự đoán trên 1 dữ liệu

svm_clf.predict([X[0]])

# Kết quả: array(['5'], dtype=object)

• Xem điểm số mà mô hình "cân nhắc" cho các đáp án

# Lấy điểm số cho từng lớp
some_digit_scores = svm_clf.decision_function([X[0]])
some_digit_scores.round(2)

"""
array([[ 3.79,  0.73,  6.06,  8.3 , -0.29,  9.3 ,  1.75,  2.77,  7.21,
         4.82]])
"""

# số 5 cao nhất là 9.3 => dự đoán là 5

Chạy OvO

Có 10 chữ số => Có 10 * (10 - 1) / 2 = 45 cặp.

Dùng decision_function() với tham số decision_function_shape = ovo để trả về tất cả 45 cặp giá trị.

svm_clf.decision_function_shape = "ovo"
some_digit_scores_ovo = svm_clf.decision_function([X[0]])
some_digit_scores_ovo.round(2)

"""
  array([[ 0.11, -0.21, -0.97,  0.51, -1.01,  0.19,  0.09, -0.31, -0.04,
            -0.45, -1.28,  0.25, -1.01, -0.13, -0.32, -0.9 , -0.36, -0.93,
             0.79, -1.  ,  0.45,  0.24, -0.24,  0.25,  1.54, -0.77,  1.11,
             1.13,  1.04,  1.2 , -1.42, -0.53, -0.45, -0.99, -0.95,  1.21,
             1.  ,  1.  ,  1.08, -0.02, -0.67, -0.14, -0.3 , -0.13,  0.25]])
"""

6. Phân tích lỗi (Error Analysis)

Đầu tiên, hãy xem xét confusion matrix. Bây giờ, có tận 10 lớp thay vì 2 nên ma trận sẽ chứa rất nhiều số và khó đọc. Giờ chúng ta sẽ vẽ ma trận ra thành các ô vuông như bàn cờ để tiện theo dõi.

Lưu ý: Đoạn code có thể chạy mất vài phút

from sklearn.metrics import ConfusionMatrixDisplay

y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
plt.rc('font', size=9)
ConfusionMatrixDisplay.from_predictions(y_train, y_train_pred, normalize="true")
plt.show()

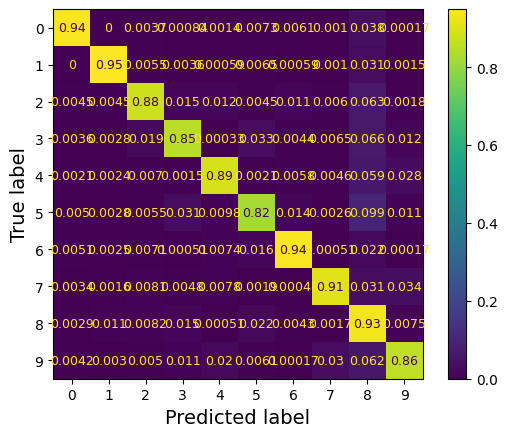
• Thêm bước chuẩn hoá và định dạng kết quả theo phần trăm

plt.rc('font', size=10)

ConfusionMatrixDisplay.from_predictions(y_train, y_train_pred,
                                        normalize="true", values_format=".0%")
plt.show()

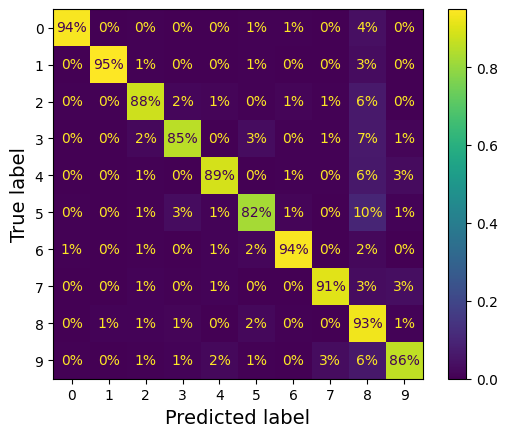
Số 5 vì lý do gì đó đang có % dự đoán đúng thấp nhất (82 %)

Lỗi phổ biến nhất mà mô hình mắc phải với hình ảnh của số 5 là phân loại nhầm chúng thành số 8 (10 %). Nhưng chỉ 2 % số 8 bị phân loại nhầm thành số 5.

Nhận thấy các số khác cũng bị sai khi dự đoán thành số 8 khá nhiều, chỉnh lại ma trận để khẳng định giả thuyết.

# Sẽ không tính các dự đoán đúng mà chỉ tính các dự đoán sai. Ta thấy nổi bật lên cột của số 8
sample_weight = (y_train_pred != y_train) # [ True False False ... False False False]
plt.rc('font', size=10)
ConfusionMatrixDisplay.from_predictions(y_train, y_train_pred,
                                        sample_weight=sample_weight,
                                        normalize="true", values_format=".0%")
plt.show()

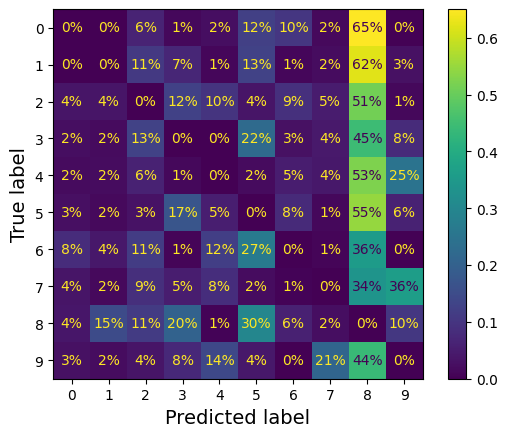
Các giá trị ở hình trên cần hiểu cho đúng. Ví dụ như hàng #7 cột #9 có giá trị 36% có nghĩa là 36% trong tổng các lỗi sai. Chứ không phải là có tận 36% số 7 bị dự đoán thành 9 (thực tế chỉ là 3%) !

• Tiếp theo, so sánh chuẩn hoá theo cột và theo hàng

fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(9, 4))
plt.rc('font', size=10)

# Chuẩn hoá theo hàng
ConfusionMatrixDisplay.from_predictions(y_train, y_train_pred, ax=axs[0],
                                        sample_weight=sample_weight,
                                        normalize="true", values_format=".0%")
axs[0].set_title("Errors normalized by row")

# Chuẩn hoá theo cột
ConfusionMatrixDisplay.from_predictions(y_train, y_train_pred, ax=axs[1],
                                        sample_weight=sample_weight,
                                        normalize="pred", values_format=".0%")
axs[1].set_title("Errors normalized by column")
plt.show()
plt.rc('font', size=14)

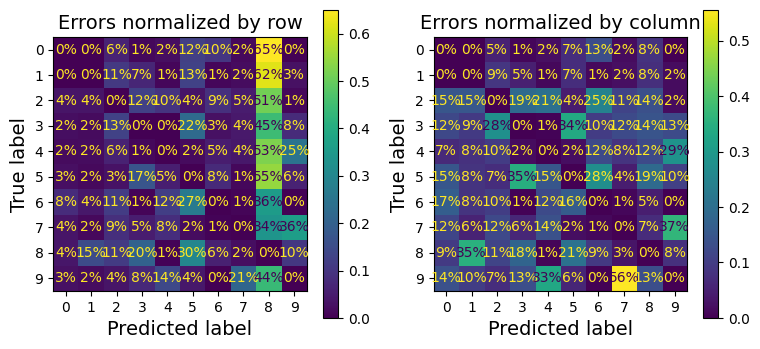
Về sự khác nhau giữa chuẩn hoá theo hàng về theo cột, xét hàng #5 cột #8

1. Chuẩn hoá theo hàng: X(5, 8) = 535 / 977 = 54.75 % => hơn 50 % dự đoán sai số 5 là nhầm thành số 8

• 535 là số lượng số 5 bị dự đoán sai thành 8
• 977 là tổng số lượng số 5 bị dự đoán sai

2. Chuẩn hoá theo cột: X(5, 8) = 535 / 2797 = 19.12 % => Hơn 19% lỗi dự đoán là 8 đến từ số 5

• 2797 là tổng số trường hợp dự đoán sai là số 8

Ngoài ra, thấy số 3 và 5 cũng hay bị nhầm lẫn với nhau

• Lọc các trường hợp

cl_a, cl_b = '3', '5'
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)] # TH dự đoán đúng là số 3
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)] # TH số 3 nhưng nhầm ra số 5
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)] # TH số 5 nhưng nhầm ra số 3
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)] # TH số 5 được dự đoán đúng

• Vẽ biểu đồ

fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(9, 4))
plt.rc('font', size=10)

# Chuẩn hoá theo hàng
ConfusionMatrixDisplay.from_predictions(y_train, y_train_pred, ax=axs[0],
                                        sample_weight=sample_weight,
                                        normalize="true", values_format=".0%")
axs[0].set_title("Errors normalized by row")

# Chuẩn hoá theo cột
ConfusionMatrixDisplay.from_predictions(y_train, y_train_pred, ax=axs[1],
                                        sample_weight=sample_weight,
                                        normalize="pred", values_format=".0%")
axs[1].set_title("Errors normalized by column")
plt.show()
plt.rc('font', size=14)

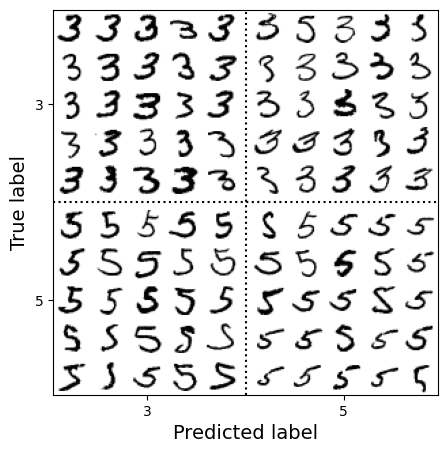
Với việc viết tay đôi khi không được "nắn nót" lắm như ở ảnh trên khiến mô hình nhận lầm giữa số 3 và số 5.

Sự khác biệt chính giữa số 3 và số 5 là vị trí của điểm nối phần trên và phần dưới. Nếu vẽ số 3 với điểm nối hơi lệch sang trái, mô hình có thể phân loại nó thành số 5, và ngược lại.

Nói cách khác, mô hình rất nhạy với sự dịch chuyển và xoay ảnh. Một cách để giảm lỗi khi dự đoán giữa số 3 và số 5 là tiền xử lý ảnh để đảm bảo ảnh được căn giữa và không bị xoay quá nhiều. Tuy nhiên, việc này không đơn giản vì cần dự đoán đúng góc xoay của mỗi ảnh.

Hoặc có thể tăng cường dữ liệu huấn luyện bằng cách tạo ra các phiên bản ảnh được dịch chuyển nhẹ hoặc xoay nhẹ. Việc này buộc mô hình học cách chịu đựng các biến đổi như vậy tốt hơn. Cách này được gọi là tăng cường dữ liệu (data augmentation) (sẽ tìm hiểu ở các phần sau).

7. Multilabel Classification

Cho đến giờ, mỗi mẫu dữ liệu luôn chỉ được gán cho một lớp duy nhất. Nhưng trong một số trường hợp, bạn có thể muốn mô hình phân loại trả về nhiều đáp án cho mỗi mẫu. Đây gọi là Multilabel Classification.

• Phân loại xem 1 số có phải là số lớn hơn 7 và là số lẻ hay không ?

import numpy as np
from sklearn.neighbors import KNeighborsClassifier

y_train_large = (y_train >= '7')
y_train_odd = (y_train.astype('int8') % 2 == 1)
y_multilabel = np.c_[y_train_large, y_train_odd]

knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_multilabel)

• Cho mô hình dự đoán sau khi đã huấn luyện

knn_clf.predict([some_digit])

# Kết quả: array([[False,  True]])

8. Multioutput Classification

Multioutput Classification là dạng tổng quát của multilabel classification. Trong đó mỗi nhãn có thể thuộc về nhiều lớp.

Ví dụ, ta xây dựng một hệ thống loại bỏ nhiễu khỏi hình ảnh. Hệ thống sẽ nhận đầu vào là một hình ảnh chữ số có nhiễu, và kỳ vọng rằng sẽ đưa ra đầu ra là một hình ảnh chữ số rõ nét

Chữ số được biểu diễn dưới dạng một mảng các pixel, giống như các hình ảnh trong tập dữ liệu MNIST.

Lưu ý: Đầu ra của mô hình là multilabel (mỗi nhãn cho mỗi pixel) và pixel có thể có nhiều giá trị (dao động từ 0 đến 255).

np.random.seed(42)

# Tạo nhiễu ngẫu nhiên cho tập huấn luyện với giá trị từ 0 đến 100 và kích thước tương ứng với dữ liệu huấn luyện
noise = np.random.randint(0, 100, (len(X_train), 784))

# Thêm nhiễu vào dữ liệu huấn luyện để tạo ra tập dữ liệu huấn luyện bị nhiễu
X_train_mod = X_train + noise

# Tạo nhiễu ngẫu nhiên cho tập kiểm tra với giá trị từ 0 đến 100 và kích thước tương ứng với dữ liệu kiểm tra
noise = np.random.randint(0, 100, (len(X_test), 784))

# Thêm nhiễu vào dữ liệu kiểm tra để tạo ra tập dữ liệu kiểm tra bị nhiễu
X_test_mod = X_test + noise

# Gán nhãn của tập huấn luyện gốc (không bị nhiễu) cho tập dữ liệu huấn luyện bị nhiễu
y_train_mod = X_train

# Gán nhãn của tập kiểm tra gốc (không bị nhiễu) cho tập dữ liệu kiểm tra bị nhiễu
y_test_mod = X_test

• Xem thử 1 ảnh trước và sau khi khử nhiễu sẽ như thế nào ?

plt.subplot(121); plot_digit(X_test_mod[0])
plt.subplot(122); plot_digit(y_test_mod[0])
plt.show()

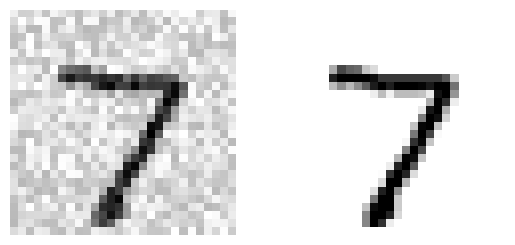
Tài liệu tham khảo

https://github.com/ageron/handson-ml3/blob/main/03_classification.ipynb