Nguyễn Văn Quân @nguyen.van.quan

1.1K 35 13

Đã đăng vào thg 5 25, 2022 4:27 SA

trong

27 phút đọc

936

Từ lý thuyết lượng tử đến Quantum Neural Network (phần 2) - Simple Quantum Neural Network

MayFest2022 Reconnection

Một số kiến thức cần nắm

Mình khuyến khích mọi người trước khi đọc bài này thì nên tìm hiểu Quantum Computing hoặc đọc bài giới thiệu cơ bản về tính toán lượng tử mà mình đã viết để có thể hiểu rõ hơn. Tuy nhiên, mình vẫn sẽ tóm tắt lại các ý chính của phần trước ở đây đồng thời có thêm một số đoạn code để các bạn dễ hình dung hơn. Ở bài viết này mình sẽ lược qua một số kiến thức tiếp theo về quantum circuit cũng như một số thao tác cơ bản với thư viện Paddle Quantum để xây dựng Quantum Neural Network vì thư viện này khá dễ dùng và tường minh, những bài viết sau mình sẽ giới thiệu đến các bạn một thư viện khác là IBM Qiskit và tập trung khai thác vào thư viện này vì tính linh hoạt và ứng dụng cao của nó khi có thể kết hợp với Pytorch để xây dựng model và can thiệp sâu vào quá trình training cũng như có thể xây dựng nhiều hướng như Quantum thuần hay Quantum - Classical,... Hơn nữa còn có thể chạy code với máy tính lượng tử được hỗ trợ bởi IBM =)) Còn một điều nữa khá quan trọng là những phần code được xây dựng với hai thư viện mà mình giới thiệu với các bạn hoàn toàn có thể chạy ở máy tính bình thường với mục đích test thuật toán và mô phỏng bởi simulator của IBM hay Baidu cung cấp, trong tương lai nếu có ý định thì chúng ta cũng hoàn toàn có thể dễ dàng request account để có thể chạy ở máy tính lượng tử thật sự.

Đặt vấn đề

Tính toán toán lượng tử (Quantum Computing) sử dụng các hiện tượng độc đáo trong vật lý lượng tử (chồng chất lượng tử, giao thoa lượng tử và rối lượng tử) để thiết kế các thuật toán và giúp giải quyết các nhiệm vụ cụ thể trong vật lý, hóa học và thuyết tối ưu hóa. Một số mô hình tính toán lượng tử hiện có bao gồm Tính toán lượng tử đoạn nhiệt (AQC) dựa trên định lý đoạn nhiệt và Tính toán lượng tử dựa trên phép measure (MBQC). Phần giới thiệu này sẽ tập trung vào mô hình vi mạch lượng tử được sử dụng rộng rãi nhất. Trong các mạch lượng tử, đơn vị tính toán cơ bản là bit lượng tử (qubit), tương tự như khái niệm bit trong máy tính cổ điển. Các bit cổ điển chỉ có thể ở một trong hai trạng thái 0 hoặc 1. Để so sánh, các qubit không chỉ có thể ở nhiều trạng thái cơ bản khác nhau mà còn ở trạng thái chồng chất. Mô hình mạch lượng tử sử dụng các cổng logic lượng tử để điều khiển trạng thái của các qubit này.

Qubit là gì?

Biểu diễn toán học

Trong cơ học lượng tử, trạng thái của hệ lượng tử hai cấp (ví dụ: spin của điện tử) có thể được biểu thị dưới dạng một vectơ trạng thái thu được thông qua các tổ hợp tuyến tính của cơ sở trực chuẩn sau đây:

$\ket{0} := \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \quad \ket{1} := \begin{bmatrix} 0 \\ 1 \end{bmatrix} \tag{1}$

Biểu diễn vectơ ở đây tuân theo ký hiệu Dirac (bra-ket) trong vật lý lượng tử. Cơ sở trực chuẩn $\{\ket{0}, \ket{1}\}$ chính là cơ sở tính toán. Về mặt vật lý, người ta có thể coi $\ket{0}$ và $\ket{1}$ lần lượt là trạng thái năng lượng cơ bản và trạng thái kích thích của một nguyên tử. Tất cả các trạng thái thuần túy có thể có của qubit có thể được coi là vectơ chuẩn hóa trong không gian Hilbert hai chiều. Hơn nữa, các trạng thái nhiều qubit có thể được biểu diễn bằng các vectơ đơn vị trong không gian Hilbert nhiều chiều mà cơ sở là tích tensor của $\{\ket{0}, \ket{1}\}$ . Ví dụ, trạng thái lượng tử 2 qubit có thể được biểu diễn bằng một vectơ đơn vị phức trong không gian Hilbert 4 chiều với cơ sở trực chuẩn:

$\left\{ \ket{00} = \ket{0}\otimes \ket{0} := \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}, \quad \ket{01} = \ket{0}\otimes \ket{1} := \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}, \quad \ket{10} = \ket{1}\otimes \ket{0} := \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix}, \quad \ket{11} = \ket{1}\otimes \ket{1} := \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} \right\} \qquad \quad (2)$

Theo quy ước, vị trí ngoài cùng bên trái trong ký hiệu ket đại diện cho qubit đầu tiên $q_0$ , vị trí thứ hai đại diện cho qubit thứ hai $q_1$ ,... .Biểu tượng $\otimes$ biểu thị phép nhân của tích tensor, phép nhân hoạt động như sau: cho hai ma trận $A_{m\times n}$ và $B_{p\times q}$ khi đó tích tensor của $A,B$ là:

$A \otimes B = \begin{bmatrix} a_{11}B & \cdots & a_{1n}B\\ \vdots & \ddots & \vdots \\ a_{m1}B & \cdots & a_{m n}B \end{bmatrix}_{(mp)\times (nq)} \tag{3}$

Bất kỳ trạng thái lượng tử qubit đơn $\ket{\psi}$ nào cũng có thể được viết dưới dạng kết hợp tuyến tính (chồng chất) của các vectơ cơ sở $\ket{0}$ và $\ket{1}$ .

$|\psi\rangle = \alpha |0\rangle + \beta |1\rangle:= \begin{bmatrix} \alpha \\ \beta \end{bmatrix}. \tag{4}$

trong đó $\alpha$ và $\beta$ là các số phức được gọi là biên độ xác suất. Theo Quy tắc Sinh trong cơ học lượng tử, xác suất để tìm thấy qubit ở trạng thái $\ket{0}$ là $|\alpha|^2$ ; và xác suất của $\ket{1}$ là $|\beta|^2$ . Vì tổng các xác suất bằng 1, nên người ta đưa ra ràng buộc: $|\alpha|^2 + |\beta|^2 = 1$ .

Biểu diễn bloch sphere

Quả cầu Bloch là một quả cầu có bán kính đơn vị. Nó được sử dụng để biểu diễn các qubit một cách trực quan. Vị trí của mỗi qubit được xác định rõ ràng thông qua các tham số $\theta$ và $\varphi$ .

$|\psi\rangle = \alpha |0\rangle + \beta |1\rangle= \cos\bigg(\frac{\theta}{2}\bigg) |0\rangle + e^{i\varphi}\sin\bigg(\frac{\theta}{2}\bigg)|1\rangle \tag{5}$

Với $0 ≤ φ < 2π$ và $0 ≤ θ < \frac{\pi}{2}$ , hay là chỉ với một nửa quả cầu ta đã có thể biểu diễn vô hạn toàn bộ các qubit

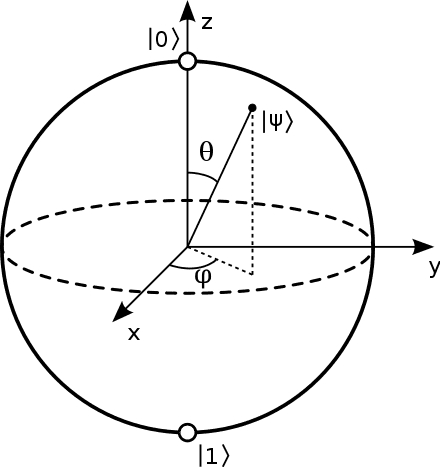
Biểu diễn bloch sphere với paddle quantum

Lý thuyết như vậy là đủ rồi, bây giờ chúng ta sẽ bắt đầu làm quen với thư viện paddle-quantum nhé. Đầu tiên để cài thư viện chúng ta chỉ cẩn chạy dòng lệnh:pip install paddle-quantum trên terminal.

Chúng ta sẽ dùng thử thư viện này để biểu diễn các trạng thái lượng tử của qubit trên bloch sphere :

from paddle_quantum.circuit import UAnsatz
from paddle_quantum.utils import plot_state_in_bloch_sphere, plot_rotation_in_bloch_sphere
import numpy as np
import paddle

# Set random seed
np.random.seed(42)
# Number of samples
num_samples = 15
# Store the sampled quantum states
state = []

for i in range(num_samples):
    
    # Create a single qubit circuit
    cir = UAnsatz(1)
    # Generate random rotation angles
    phi, theta, omega = 2 * np.pi * np.random.uniform(size=3)
    phi = paddle.to_tensor(phi, dtype='float64')
    theta = paddle.to_tensor(theta, dtype='float64')
    omega = paddle.to_tensor(omega, dtype='float64')
    
    # Quantum gate operation
    cir.rz(phi, 0)
    cir.ry(theta, 0)
    cir.rz(omega, 0)
    
    # Store the sampled quantum states
    state.append(cir.run_state_vector())

# Call the Bloch sphere display function, enter the state parameter, and display the vector.
plot_state_in_bloch_sphere(state, show_arrow=True, save_gif=True)

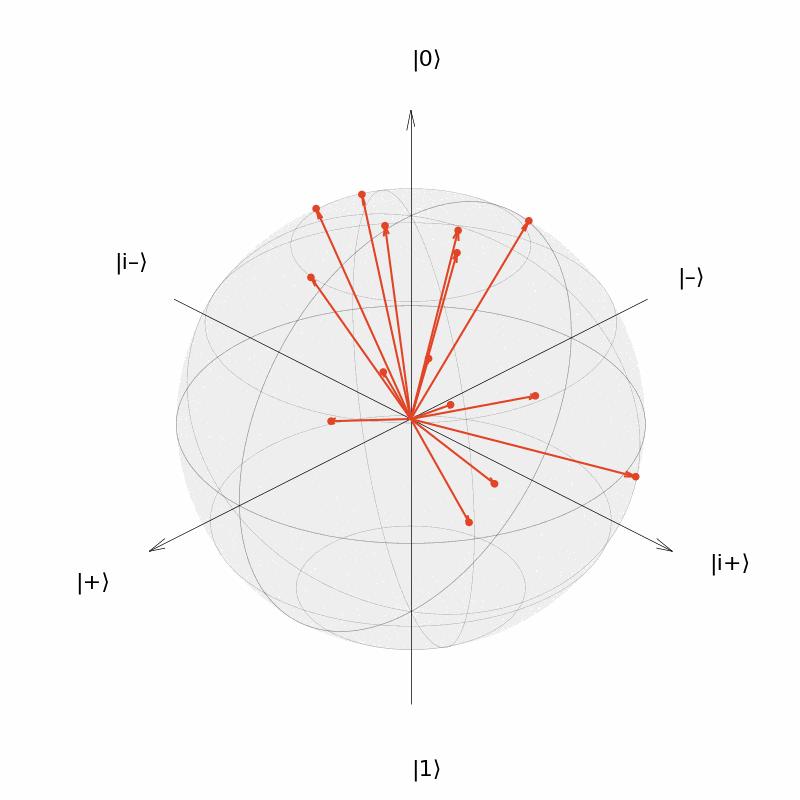
Như trong hình trên, mình đã lấy mẫu ngẫu nhiên 15 lần để tạo ra 15 trạng thái lượng tử qubit đơn khác nhau và hiển thị lần lượt 15 trạng thái lượng tử này trên quả cầu Bloch.

Làm thế nào để mô tả "quỹ đạo" chuyển động quay của một trạng thái lượng tử qubit đơn trên quả cầu Bloch? Lấy ví dụ toán tử đơn nhất của một qubit là phép quay một vectơ trên hình cầu Bloch. Trạng thái ban đầu của mạch lượng tử tương ứng với vị trí ban đầu của vectơ đầu trên quả cầu Bloch, và trạng thái cuối cùng của mạch lượng tử tương ứng với vị trí cuối cùng của vectơ sau khi quay trên quả cầu Bloch. Ta xét trạng thái lượng tử của $\ket{0}$ qua cổng quay $R_y(\frac{\pi}{4})$ và $R_z(\frac{\pi}{2})$ là trạng thái ban đầu, và trạng thái sau khi qua cổng $U3(\theta = \frac{\pi}{2}, \phi = \frac{7\pi}{8}, \lambda = 2\pi)$ là cuối cùng. Code mô tả chuyển động của vector:

# Set the initial state of the quantum state
cir.ry(paddle.to_tensor(np.pi/4, dtype="float64"), 0)
cir.rz(paddle.to_tensor(np.pi/2, dtype="float64"), 0)
init_state = cir.run_density_matrix()

# Unitary operator operation to be performed
theta = np.pi/2
phi = 7*np.pi/8
lam = 2*np.pi
rotating_angle = [theta, phi, lam]

# Call Bloch sphere display function，input init_state，rotating_angle
plot_rotation_in_bloch_sphere(init_state, rotating_angle)

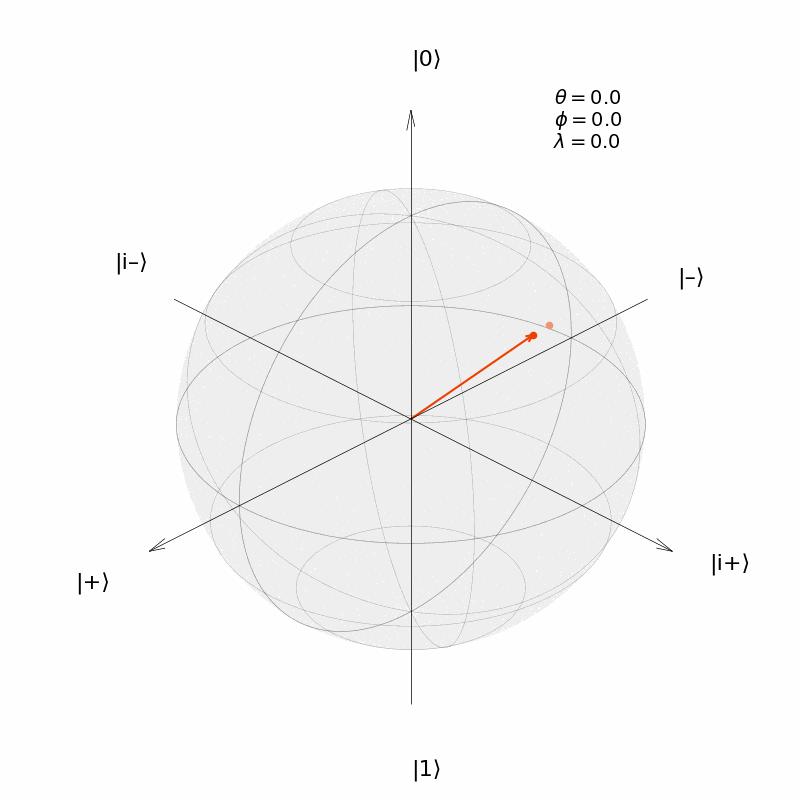
Cổng Logic Quantum

Trong máy tính cổ điển, chúng ta có thể áp dụng các phép toán logic cơ bản (cổng NOT, cổng NAND, cổng XOR, cổng AND và cổng OR) trên các bit cổ điển và kết hợp chúng thành các phép toán phức tạp hơn. Máy tính lượng tử có một tập hợp các phép toán logic hoàn toàn khác, chúng được gọi là các cổng lượng tử và chúng ta không thể biên dịch các chương trình C ++ hiện có trên máy tính lượng tử. Bởi vì máy tính cổ điển và máy tính lượng tử có cấu trúc cổng logic khác nhau, các thuật toán lượng tử cần được xây dựng bằng cách sử dụng cổng lượng tử. Về mặt toán học, một cổng lượng tử có thể được biểu diễn như một ma trận đơn nguyên. Các phép toán đơn nguyên có thể bảo toàn độ dài vectơ - đây là thuộc tính mà chúng ta mong muốn. Ma trận đơn nguyên được định nghĩa như sau:

$U^{\dagger}U = UU^{\dagger} = I, \quad \text{và} \quad \Vert |\psi\rangle \Vert = \Vert U|\psi\rangle\Vert = 1. \tag{6}$

Trong đó $U^{\dagger}$ là chuyển vị liên hợp của $U$ và là đại diện cho ma trận đơn vị.

Vậy ý nghĩa vật lý của việc biểu diễn các cổng lượng tử dưới dạng ma trận đơn nguyên là gì? Điều này ngụ ý rằng tất cả các cổng lượng tử đều có thể đảo ngược. Đối với bất kỳ cổng logic $U$ nào, người ta luôn có thể tìm thấy cổng đảo $U^{\dagger}$ tương ứng. Ngoài ra, ma trận đơn nguyên phải là ma trận vuông, vì đầu vào và đầu ra của phép toán lượng tử yêu cầu cùng một lượng qubit. Cổng lượng tử tác động lên $n$ qubit có thể được viết dưới dạng $2^n \times 2^n$ ma trận đơn nguyên. Các cổng lượng tử phổ biến nhất hoạt động trên một hoặc hai qubit, giống như các cổng logic cổ điển.

Cổng đơn qubit

Tiếp theo đây mình sẽ giới thiệu đến các bạn bộ 3 ma trận Pauli $\{X, Y, Z\}$ tương ứng với 3 cổng quay $\{R_x, R_y, R_z\}$ và sau đó sẽ là cổng Hadamard $H$ . Đầu tiên chúng ta nói qua về cổng NOT - một cổng khá cơ bản và quan trọng ở cả tính toán cổ điển và lượng tử,

$X := \begin{bmatrix} 0 &1 \\ 1 &0 \end{bmatrix}. \tag{7}$

Cổng Pauli $X$ còn được gọi là cổng NOT. Cổng này có ý nghĩa là tạo ra trang thái "ngược" với trạng thái $\ket{0}$ hoặc $\ket{1}$ đầu vào, tương đương với việc quay trạng thái qubit trên mặt cầu Bloch sang điểm đối diện với nó trên mặt cầu và các thao tác tính toán với cổng này đơn giản chỉ là nhân ma trận với vector cột :

$X |0\rangle := \begin{bmatrix} 0 &1 \\ 1 &0 \end{bmatrix} \begin{bmatrix} 1 \\0 \end{bmatrix} =\begin{bmatrix} 0 \\1 \end{bmatrix} = |1\rangle, \quad \text{và} \quad X |1\rangle := \begin{bmatrix} 0 &1 \\ 1 &0 \end{bmatrix} \begin{bmatrix} 0 \\1 \end{bmatrix} =\begin{bmatrix} 1 \\0 \end{bmatrix}=|0\rangle.$

Xét trên quả cầu bloch, khi ma trận $X$ này tính toán với trạng thái của 1 qubit thì tương ứng với một phép quay ở trục $x$ của quả cầu với góc $\pi$ . Điều này lý giải tại sao ma trận $X$ được biểu diễn dưới dạng $R_x(\pi)$ ( được phân biệt với pha toàn cục $e^{-i\pi/2} = -i$ ). Hai ma trận Pauli khác là $Y \text{ và } Z$ cũng có thể được giải thích theo cách tương tự (đại biểu cho phép quay quanh trục $y \text{ và } z$ với góc $\pi$ :

$Y := \begin{bmatrix} 0 &-i \\ i &0 \end{bmatrix}, \quad \text{ và} \quad Z := \begin{bmatrix} 1 &0 \\ 0 &-1 \end{bmatrix}. \tag{9}$

Nói chung, bất kỳ cổng lượng tử nào quay một góc $\theta$ quanh trục tương ứng trên hình cầu Bloch có thể được biểu thị như sau :

$R_x(\theta) := \begin{bmatrix} \cos \frac{\theta}{2} &-i\sin \frac{\theta}{2} \\ -i\sin \frac{\theta}{2} &\cos \frac{\theta}{2} \end{bmatrix} ,\quad R_y(\theta) := \begin{bmatrix} \cos \frac{\theta}{2} &-\sin \frac{\theta}{2} \\ \sin \frac{\theta}{2} &\cos \frac{\theta}{2} \end{bmatrix} ,\quad R_z(\theta) := \begin{bmatrix} e^{-i\frac{\theta}{2}} & 0 \\ 0 & e^{i\frac{\theta}{2}} \end{bmatrix}. \tag{10}$

Mình sẽ ví dụ tạo cổng $R_x$ với paddle, các cổng $R_y,R_z$ hoàn toàn tương tự:

# Set the angle parameter theta = pi
theta = np.pi

# Set the number of qubits required for calculation
num_qubits = 1

# Initialize the single-bit quantum circuit
cir = Circuit(num_qubits)

# Apply an Rx rotation gate to the first qubit (q0), the angle is pi
cir.rx(0, param=theta)

# Convert to numpy.ndarray
# Print out this quantum gate
print('The matrix representation of quantum gate is:')
print(cir.unitary_matrix().numpy())

Output:


The matrix representation of quantum gate is:
[[-4.371139e-08+0.j  0.000000e+00-1.j]
 [ 0.000000e+00-1.j -4.371139e-08+0.j]]

Ngoài các cổng xoay nói trên, cổng đơn qubit cuối cùng và cũng là quan trọng nhất mà mình muốn nói đến là cổng Hadamard. Xét trên quả cầu Bloch thì cổng này bao gồm hai phép quay riêng biệt, đầu tiên quay một góc $\pi$ quanh trục $z$ và sau đó quay góc $\pi/2$ quanh trục $y$ . Cổng này có ý nghĩa là tạo ra trang thái "trộn" đều từ trạng thái $\ket{0}$ hoặc $\ket{1}$ đầu vào. Biểu diễn ma trận của nó như sau :

$H := \frac{1}{\sqrt{2}}\begin{bmatrix} 1 &1 \\ 1 &-1 \end{bmatrix}. \tag{11}$

Một mạch lượng tử tạo bởi các cổng Hadamard như hình trên được gọi là mạch khởi tạo thanh ghi lượng tử. Đầu ra của mạch này là:

$\ \ket{\psi} =\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})...\frac{1}{\sqrt{2}}(\ket{0}+\ket{1}) \\ =\frac{1}{2^{N/2}}(\ket{00...0}+\ket{00...1}+...+\ket{11...1})$

Ở đây, $N$ là số qubit đầu vào. Như vậy đầu ra của mạch khởi tạo thanh ghi lượng tử, với đầu vào $N$ qubit ở trạng thái $\ket{0}$ , là trạng thái "trộn" đều của tất cả các véc tơ trong hệ cơ sở của không gian $2^N$ chiều chứa các trạng thái của $N$ qubit.

Cổng đa qubit

Như đã nói ở bài trước thì multiple qubit chính là sự kết hợp của nhiều qubit đơn lẻ tạo thành một hệ đa qubit và một hệ đa qubit như vậy cần các cổng đa qubit để có thể tương tác với nhau. Chúng ta sẽ bắt đầu phần này với việc tìm hiểu một cổng logic khá cơ bản đó là CNOT.

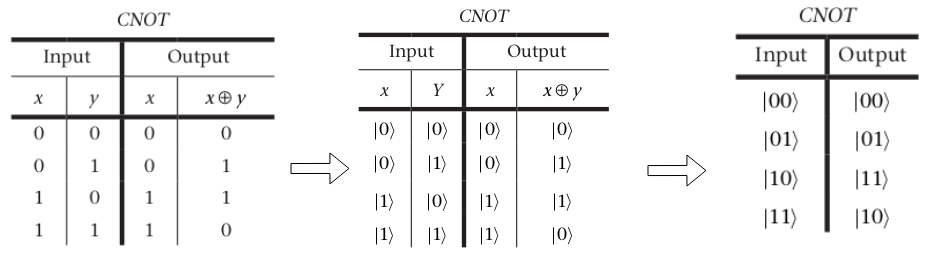
Untitled Diagram.drawio(1).png

$\text{CNOT} |00\rangle = |00\rangle, \quad \text{CNOT} |01\rangle = |01\rangle, \quad \text{CNOT} |10\rangle = |11\rangle, \quad \text{CNOT} |11\rangle = |10\rangle.$

Cách hoạt động của cổng CNOT khá dễ hình dung, đầu vào của cổng CNOT gồm 2 Qubit: qubit thứ nhất là qubit Điều khiển (control), qubit thứ hai là qubit mục tiêu (target). Qubit Điều khiển sẽ không bị thay đổi sau khi qua cổng CNOT, qubit Mục tiêu sẽ bị đảo ngược khi và chỉ khi Qubit Điều khiển là 1, giá trị của Qubit Mục tiêu chính là kết quả của phép XOR giữa hai Qubit đầu vào. Nhưng vẫn có một điều mà chúng ta cần lưu tâm, nếu qubit điều khiển là $\ket{0}$ hoặc $\ket{1}$ thì những điều mình nói ở trên là đúng. Vậy nếu nó nằm ngoài 2 trường hợp trên thì sao ? Cùng xem qua 3 ví dụ này nhé!

Ví dụ 1: Xét qubit $|\psi\rangle=a|0\rangle+b|1\rangle=\left[\begin{array}{}a \\ b\end{array}\right]$ là qubit mục tiêu và $\ket{1}$ là qubit điều khiển. Ta sẽ dùng ma trận để tính kết quả của CNOT $\ket{1, \psi}$
$\text{Ta có: }|1, \psi\rangle=a|10\rangle+b|11\rangle=\left[\begin{array}{l}0 \\ 0 \\ a \\ b\end{array}\right]$

$~~~~~~~~~$ $\mathrm{CNOT}$ $|1, \psi\rangle=\left[\begin{array}{llll}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0\end{array}\right]\left[\begin{array}{l}0 \\ 0 \\ a \\ b\end{array}\right]=\left[\begin{array}{l}0 \\ 0 \\ b \\ a\end{array}\right]=|1, \phi\rangle$ . Với $|\phi\rangle=b|0\rangle+a|1\rangle$ .

$~~~~~~~~~~$ Vậy $\ket{1, \psi}$ sau khi đi qua CNOT sẽ thành $\ket{1, \phi}$

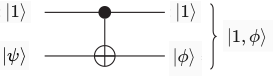
Untitled Diagram.drawio(2).png

Ví dụ 2 : Xét qubit $\ket{1}$ là qubit mục tiêu và $\psi = \frac{1}{\sqrt{2}}\ket{0}+\frac{1}{\sqrt{2}}\ket{1}$ là qubit điều khiển.
$\text{Ta có: }|\psi, 1\rangle=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\otimes|1\rangle=\frac{1}{\sqrt{2}}(|01\rangle+|11\rangle)=\left[\begin{array}{c}0 \\ \frac{1}{\sqrt{2}} \\ 0 \\ \frac{1}{\sqrt{2}}\end{array}\right] .$

$~~~~~~~~~\mathrm{CNOT}|\psi, 1\rangle=\left[\begin{array}{cccc}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0\end{array}\right]\left[\begin{array}{c}0 \\ \frac{1}{\sqrt{2}} \\ 0 \\ \frac{1}{\sqrt{2}}\end{array}\right]=\left[\begin{array}{c}0 \\ \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ 0\end{array}\right]=|\phi\rangle$
$~~~~~~~~~~\ket{\phi}=\frac{1}{\sqrt{2}}(\ket{01}+\ket{10})$ . Như vậy hệ $\ket{\psi}$ đã bị rối lượng tử sau khi đi qua cổng CNOT

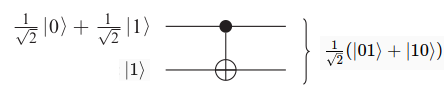
Untitled Diagram.drawio(3).png

Ví dụ 3 : Xét hệ rối lượng tử $|\phi\rangle=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)=\left[\begin{array}{c}\frac{1}{\sqrt{2}} \\ 0 \\ 0 \\ \frac{1}{\sqrt{2}}\end{array}\right]$ . Cho hệ đi qua cổng CNOT:
$\mathrm{CNOT}|\phi\rangle=\left[\begin{array}{cccc}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0\end{array}\right]\left[\begin{array}{c}\frac{1}{\sqrt{2}} \\ 0 \\ 0 \\ \frac{1}{\sqrt{2}}\end{array}\right]=\left[\begin{array}{c}\frac{1}{\sqrt{2}} \\ 0 \\ \frac{1}{\sqrt{2}} \\ 0\end{array}\right]=|\psi\rangle$ .

$~~~~~~~~~~|\psi\rangle=\frac{1}{\sqrt{2}}(|00\rangle+|10\rangle)=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)|0\rangle$ . Như vậy hệ $\phi$ đã được gỡ rối.

Ba ví dụ trên đã minh họa cho chúng ta 3 cách sử dụng của cổng CNOT đó là : đảo bit có điều kiện, tạo rối lượng tử, gỡ rối lượng tử. Ngoài ra còn một số cổng nữa mình không tiện đề cập ở đây, các bạn có thể vào link wiki này để tìm hiểu.

$~~~~~~~~~~~~~~~~~~~~~~~~$ https://en.wikipedia.org/wiki/Quantum_logic_gate

Measurement

Đối với hệ lượng tử hai cấp, chẳng hạn như spin của electron, nó có thể quay lên $\uparrow$ hoặc quay xuống $\downarrow$ , tương ứng với trạng thái $\ket{0}$ và $\ket{1}$ . Như đã đề cập trước đây, electron có thể ở trạng thái chồng chất của spin $\uparrow$ và $\downarrow$ : $|\psi\rangle =\alpha |0\rangle + \beta |1\rangle$ và phép measurement sẽ giúp chúng ta hiểu thêm về trạng thái chồng chất là gì. Cần lưu ý rằng phép measurement trong cơ học lượng tử thường mang tính thống kê xác suất hơn là một phép measurement đơn lẻ. Điều này là do bản chất của các phép measurement trong vật lý lượng tử, nó làm sụp đổ trạng thái lượng tử quan sát được. Ví dụ, nếu chúng ta measure một electron ở trạng thái $|\psi\rangle =\alpha |0\rangle + \beta |1\rangle$ , chúng ta sẽ có xác suất $|\alpha|^2$ thu được kết quả measure spin up, và sau khi measure, trạng thái lượng tử chuyển sang trạng thái sau đo $|0\rangle$ . Tương tự, chúng ta cũng có xác suất $|\beta|^2$ để có được trạng thái $|1\rangle$ quay xuống sau khi measure. Vì vậy, nếu chúng ta muốn nhận được giá trị chính xác của $\alpha$ , chỉ một thử nghiệm thì rõ ràng là không đủ. Chúng ta cần chuẩn bị rất nhiều electron ở trạng thái chồng chất, measure spin của từng electron, rồi đếm tần số. Phép measure có một vị trí đặc biệt trong cơ học lượng tử và mạng neuron lượng tử. Nếu bạn đọc cảm thấy khó hiểu, các bạn có thể tham khảo link Measurement in quantum mechanics để tìm hiểu kỹ hơn

Quantum Neural Network

Mạng nơron lượng tử là một lớp con của các thuật toán biến đổi lượng tử , bao gồm các mạch lượng tử có chứa các hoạt động cổng lượng tử tham số hóa. Dữ liệu đầu tiên được mã hóa thành trạng thái lượng tử thông qua các cổng lượng tử hoặc bản đồ đặc trưng. Việc lựa chọn bản đồ đặc trưng thường hướng tới việc nâng cao hiệu suất của mô hình lượng tử và thường không được tối ưu hóa cũng như không được training. Khi dữ liệu được mã hóa sang trạng thái lượng tử, một mô hình biến thể chứa các cổng tham số hóa sẽ được áp dụng và tối ưu hóa cho một task cụ thể. Điều này được thực hiện thông qua tối thiểu hàm mất mát tương tự như những bài toán machine learning thông thường, sau đó đầu ra của mô hình lượng tử được measure thông qua hàm Hamiltonian như là các cổng Pauli chẳng hạn.

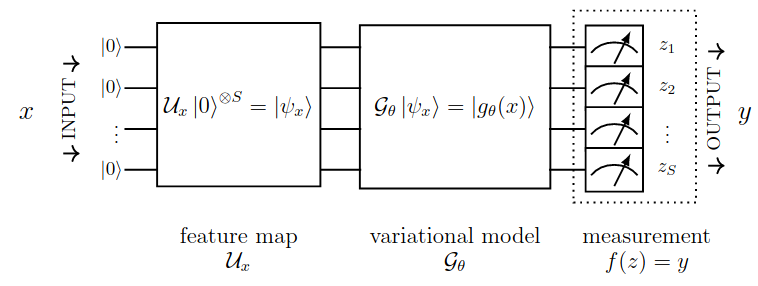
Tổng quan về quantum neural network: đầu vào $x \in \mathbb{R}^{s_{\text {in }}}$ đầu tiên được mã hóa vào không gian lượng tử $Hilbert$ $S$ -qubit thông qua khối feature mapping $\left|\psi_{x}\right\rangle:=\mathcal{U}_{x}|0\rangle^{\otimes S}$ (một mạch tham số hóa lượng tử được định nghĩa sẵn). Dữ liệu sau khi mã hóa sẽ được "học" bởi khối variational model hay cũng chính là các mạch tham số hóa lượng tử $| g _ { \theta } \left ( x \right ) \rangle : = G _ { \theta } | \psi _ { x } \rangle$ . Đầu ra cuối cùng được đưa qua phép measurement và hậu xử lý để trích xuất output của model và mapping về dạng classical.

QClassifier

Như vậy là chúng ta đã đi qua những phần lý thuyết cơ bản và cần thiết để có thể xây dựng một mạng neuron lượng tử đơn giản, bây giờ sẽ đi vào ví dụ để có thể trực quan hóa những gì chúng ta vừa tìm hiểu nhé !

Mình sẽ tiến hành xây dựng pipeline cho bài toán adhoc phân loại đơn giản. Đầu tiên ta cần import các thư viện cần thiết:

# Import numpy,paddle and paddle_quantum
import numpy as np
import paddle
import paddle_quantum

# To construct quantum circuit
from paddle_quantum.ansatz import Circuit

# Some functions
from numpy import pi as PI
from paddle import matmul, transpose, reshape  # paddle matrix multiplication and transpose
from paddle_quantum.qinfo import pauli_str_to_matrix # N qubits Pauli matrix
from paddle_quantum.linalg import dagger  # complex conjugate

# Plot figures, calculate the run time
from matplotlib import pyplot as plt
import time

Khai báo các tham số được sử dụng cho model :

# Parameters for generating the data set
Ntrain = 200        # Specify the training set size
Ntest = 100         # Specify the test set size
boundary_gap = 0.5  # Set the width of the decision boundary
seed_data = 2       # Fixed random seed required to generate the data set
# Parameters for training
N = 4               # Number of qubits required
DEPTH = 1           # Circuit depth
BATCH = 20          # Batch size during training
EPOCH = int(200 * BATCH / Ntrain)
                    # Number of training epochs, the total iteration number "EPOCH * (Ntrain / BATCH)" is chosen to be about 200
LR = 0.01           # Set the learning rate
seed_paras = 19     # Set random seed to initialize various parameters

Data processing

Ở ví dụ này mình sẽ dùng bộ dữ liệu của paper Supervised learning with quantum enhanced feature spaces Hàm khởi tạo dữ liệu cho bài toán phân loại nhị phân:

# Generate a binary classification data set with circular decision boundary
def circle_data_point_generator(Ntrain, Ntest, boundary_gap, seed_data):
    """
    :param Ntrain: number of training samples
    :param Ntest: number of test samples
    :param boundary_gap: value in (0, 0.5), means the gap between two labels
    :param seed_data: random seed
    :return: 'Ntrain' samples for training and
             'Ntest' samples for testing
    """
    # Generate "Ntrain + Ntest" pairs of data, x for 2-dim data points, y for labels.
    # The first "Ntrain" pairs are used as training set, the last "Ntest" pairs are used as testing set
    train_x, train_y = [], []
    num_samples, seed_para = 0, 0
    while num_samples < Ntrain + Ntest:
        np.random.seed((seed_data + 10) * 1000 + seed_para + num_samples)
        data_point = np.random.rand(2) * 2 - 1  # 2-dim vector in range [-1, 1]

        # If the modulus of the data point is less than (0.7 - gap), mark it as 0
        if np.linalg.norm(data_point) < 0.7-boundary_gap / 2:
            train_x.append(data_point)
            train_y.append(0.)
            num_samples += 1

        # If the modulus of the data point is greater than (0.7 + gap), mark it as 1
        elif np.linalg.norm(data_point) > 0.7 + boundary_gap / 2:
            train_x.append(data_point)
            train_y.append(1.)
            num_samples += 1
        else:
            seed_para += 1

    train_x = np.array(train_x).astype("float64")
    train_y = np.array([train_y]).astype("float64").T

    print("The dimensions of the training set x {} and y {}".format(np.shape(train_x[0:Ntrain]), np.shape(train_y[0:Ntrain])))
    print("The dimensions of the test set x {} and y {}".format(np.shape(train_x[Ntrain:]), np.shape(train_y[Ntrain:])), "\n")

    return train_x[0:Ntrain], train_y[0:Ntrain], train_x[Ntrain:], train_y[Ntrain:]

Ở đây mình sẽ tạo training set là 200 mẫu và test set là 100 mẫu, sau đó visualize dữ liệu để dễ hình dung hơn nhé :

def data_point_plot(data, label):
    """
    :param data: shape [M, 2], means M 2-D data points
    :param label: value 0 or 1
    :return: plot these data points
    """
    dim_samples, dim_useless = np.shape(data)
    plt.figure(1)
    for i in range(dim_samples):
        if label[i] == 0:
            plt.plot(data[i][0], data[i][1], color="r", marker="o")
        elif label[i] == 1:
            plt.plot(data[i][0], data[i][1], color="b", marker="o")
    plt.show()
# Generate data set
train_x, train_y, test_x, test_y = circle_data_point_generator(
        Ntrain, Ntest, boundary_gap, seed_data)

# Visualization
print("Visualization of {} data points in the training set: ".format(Ntrain))
data_point_plot(train_x, train_y)
print("Visualization of {} data points in the test set: ".format(Ntest))
data_point_plot(test_x, test_y)

The dimensions of the training set x (200, 2) and y (200, 1)

The dimensions of the test set x (100, 2) and y (100, 1)

Visualization of 200 data points in the training set:

Visualization of 100 data points in the test set:

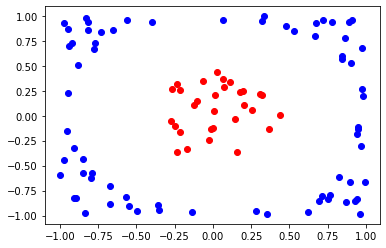
Khác với học máy cổ điển, mạng neuron lượng tử cần phải xem xét nhiều hơn đến việc tiền xử lý dữ liệu. Chúng ta cần thêm một bước để chuyển đổi dữ liệu cổ điển thành dữ liệu lượng tử trước khi chạy mô phỏng thuật toán. Tiếp theo đây mình sẽ sử dụng phương pháp "Angle Encoding" để mã hóa dữ liệu sang không gian $Hilbert$ .

Đầu tiên chúng ta cần quyết định xem cần sử dụng bao nhiêu qubit, bởi vì dữ liệu mình sử dụng chỉ có 2 chiều $\{x^{k} = (x^{k}_0, x^{k}_1)\}$ , theo như paper Quantum Circuit Learning thì mình sẽ cần ít nhất 2 qubit để mã hóa dữ liệu. Sau đó đưa $\{x^{k}\}$ qua một tổ hợp cổng lượng tử $U(x^{k})$ và xử lý dựa trên trạng thái khởi tạo $|00\rangle$ . Thông qua cách này, mình đã mã hóa được dữ liệu $|\psi_{\rm in}\rangle$ từ không gian 2 chiều ở hệ $Descartes$ sang không gian lượng tử $Hilbert$ :

$|\psi_{\rm in}\rangle = U(x)|00\rangle = \frac{1}{2} \begin{bmatrix} 1-i &0 &-1+i &0 \\ 0 &1+i &0 &-1-i \\ 1-i &0 &1-i &0 \\ 0 &1+i &0 &1+i \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} = \frac{1}{2} \begin{bmatrix} 1-i \\ 0 \\ 1-i \\ 0 \end{bmatrix}.$

# Gate: rotate around Y-axis, Z-axis with angle theta
def Ry(theta):
    """
    :param theta: parameter
    :return: Y rotation matrix
    """
    return np.array([[np.cos(theta / 2), -np.sin(theta / 2)],
                     [np.sin(theta / 2), np.cos(theta / 2)]])

def Rz(theta):
    """
    :param theta: parameter
    :return: Z rotation matrix
    """
    return np.array([[np.cos(theta / 2) - np.sin(theta / 2) * 1j, 0],
                     [0, np.cos(theta / 2) + np.sin(theta / 2) * 1j]])

# Classical -> Quantum Data Encoder
def datapoints_transform_to_state(data, n_qubits):
    """
    :param data: shape [-1, 2]
    :param n_qubits: the number of qubits to which
    the data transformed
    :return: shape [-1, 1, 2 ^ n_qubits]
        the first parameter -1 in this shape means can be arbitrary. In this tutorial, it equals to BATCH.
    """
    dim1, dim2 = data.shape
    res = []
    for sam in range(dim1):
        res_state = 1.
        zero_state = np.array([[1, 0]])
        # Angle Encoding
        for i in range(n_qubits):
            # For even number qubits, perform Rz(arccos(x0^2)) Ry(arcsin(x0))
            if i % 2 == 0:
                state_tmp=np.dot(zero_state, Ry(np.arcsin(data[sam][0])).T)
                state_tmp=np.dot(state_tmp, Rz(np.arccos(data[sam][0] ** 2)).T)
                res_state=np.kron(res_state, state_tmp)
            # For odd number qubits, perform Rz(arccos(x1^2)) Ry(arcsin(x1))
            elif i% 2 == 1:
                state_tmp=np.dot(zero_state, Ry(np.arcsin(data[sam][1])).T)
                state_tmp=np.dot(state_tmp, Rz(np.arccos(data[sam][1] ** 2)).T)
                res_state=np.kron(res_state, state_tmp)
        res.append(res_state)
    res = np.array(res, dtype=paddle_quantum.get_dtype())
    
    return res

Dữ liệu sau khi được encode :

print("As a test, we enter the classical information:")
print("(x_0, x_1) = (1, 0)")
print("The 2-qubit quantum state output after encoding is:")
print(datapoints_transform_to_state(np.array([[1, 0]]), n_qubits=2))

Build Quantum Neural Network

Để thuận tiện thì chúng ta sẽ gọi mạng lượng tử tham số hóa là $U(\boldsymbol{\theta})$ . Tương tự như các mạng neuron cổ điển, chúng ta hoàn toàn có thể tự định nghĩa cấu trúc của mạng neuron lượng tử thông qua các cổng logic lượng tử. Sau khi có được dữ liệu đã qua mã hóa $|\psi_{\rm in}\rangle$ ta sẽ đưa nó vào mạng neuron lượng tử, thực chất chỉ là một phép nhân ma trận đơn nhất với vector đầu vào để lấy trạng thái quantum đầu ra $|\varphi\rangle$

$|\psi_{\rm out}\rangle = U(\boldsymbol{\theta})|\psi_{\rm in}\rangle.$

Giả sử toàn bộ tham số $\theta = \pi$ ta sẽ có trạng thái đầu ra như sau :

$|\psi_{\rm out}\rangle = U(\boldsymbol{\theta} =\pi)|\psi_{\rm in}\rangle = \begin{bmatrix} 0 &0 &-1 &0 \\ -1 &0 &0 &0 \\ 0 &1 &0 &0 \\ 0 &0 &0 &1 \end{bmatrix} \cdot \frac{1}{2} \begin{bmatrix} 1-i \\ 0 \\ 1-i \\ 0 \end{bmatrix} = \frac{1}{2} \begin{bmatrix} -1+i \\ -1+i \\ 0 \\ 0 \end{bmatrix}.$

Measurement

Sau khi đi qua PQC $U(\theta)$ , dữ liệu lượng tử trở thành $\lvert \psi_{\rm out}\rangle^k = U(\theta)\lvert \psi_{\rm in} \rangle^k$ . Để có được nhãn của dữ liệu, chúng ta cần measure trạng thái lượng tử mới để thu được dữ liệu classical. Những dữ liệu classica này sau đó sẽ được sử dụng để tính toán hàm mất mát $\mathcal{L}(\boldsymbol{\theta})$ . Cuối cùng, dựa trên thuật toán gradient descent, ta liên tục cập nhật các thông số PQC và tối ưu hóa hàm mất mát. Giá trị mà chúng ta đạt được sau phép measure :

$\langle Z \rangle = \langle \psi_{\rm out} |Z\otimes I| \psi_{\rm out}\rangle = \frac{1}{2} \begin{bmatrix} -1-i \quad -1-i \quad 0 \quad 0 \end{bmatrix} \begin{bmatrix} 1 &0 &0 &0 \\ 0 &1 &0 &0 \\ 0 &0 &-1 &0 \\ 0 &0 &0 &-1 \end{bmatrix} \cdot \frac{1}{2} \begin{bmatrix} -1+i \\ -1+i \\ 0 \\ 0 \end{bmatrix} = 1.$

Thông thường đầu ra $\langle Z \rangle$ sẽ nằm trong khoảng $[-1,1]$ . Để đầu ra này khớp với nhãn đã định nghĩa trước $y^{k} \in \{0,1\}$ , ta sẽ cần 1 hàm ánh xạ đơn giản:

$\tilde{y}^{k} = \frac{\langle Z \rangle}{2} + \frac{1}{2} + bias \quad \in [0, 1].$

Sau khi ánh xạ, chúng ta có thể coi $\tilde{y}^{k}$ là nhãn mà cần tìm với $\tilde{y}^{k}< 0.5$ tương ứng nhãn 0 và $\tilde{y}^{k}\geq 0.5$ tương ứng nhãn 1. Toàn bộ quá trình từ bước xử lý dữ liệu đến tính toán đầu ra có thể mô tả như sau:

$x^{k} \rightarrow |\psi_{\rm in}\rangle^{k} \rightarrow U(\boldsymbol{\theta})|\psi_{\rm in}\rangle^{k} \rightarrow |\psi_{\rm out}\rangle^{k} \rightarrow ^{k}\langle \psi_{\rm out} |Z\otimes I\cdots \otimes I| \psi_{\rm out} \rangle^{k} \rightarrow \langle Z \rangle \rightarrow \tilde{y}^{k}.$

Loss function

Hàm loss được tính toán như sau :

$\mathcal{L}_{i} = \sum_{k=1}^{BATCH} \frac{1}{BATCH} |y^{i,k} - \tilde{y}^{i,k}|^2$

Quantum Neural Network:

# Generate Pauli Z operator that only acts on the first qubit
# Act the identity matrix on rest of the qubits
def Observable(n):
    r"""
    :param n: number of qubits
    :return: local observable: Z \otimes I \otimes ...\otimes I
    """
    Ob = pauli_str_to_matrix([[1.0, 'z0']], n)

    return Ob

# Build the computational graph
class Opt_Classifier(paddle_quantum.gate.Gate):
    """
    Construct the model net
    """
    def __init__(self, n, depth, seed_paras=1):
        # Initialization, use n, depth give the initial PQC
        super(Opt_Classifier, self).__init__()
        self.n = n
        self.depth = depth
        # Initialize bias
        self.bias = self.create_parameter(
            shape=[1],
            default_initializer=paddle.nn.initializer.Normal(std=0.01),
            dtype='float32',
            is_bias=False)
        
        self.circuit = Circuit(n)
        # Build a generalized rotation layer
        for i in range(n):
            self.circuit.rz(qubits_idx=i)
            self.circuit.ry(qubits_idx=i)
            self.circuit.rz(qubits_idx=i)

        # The default depth is depth = 1
        # Build the entangleed layer and Ry rotation layer
        for d in range(3, depth + 3):
            # The entanglement layer
            for i in range(n-1):
                self.circuit.cnot(qubits_idx=[i, i + 1])
            self.circuit.cnot(qubits_idx=[n-1, 0])
            # Add Ry to each qubit
            for i in range(n):
                self.circuit.ry(qubits_idx=i)

    # Define forward propagation mechanism, and then calculate loss function and cross-validation accuracy
    def forward(self, state_in, label):
        """
        Args:
            state_in: The input quantum state, shape [-1, 1, 2^n] -- in this tutorial: [BATCH, 1, 2^n]
            label: label for the input state, shape [-1, 1]
        Returns:
            The loss:
                L = 1/BATCH * ((<Z> + 1)/2 + bias - label)^2
        """
        # Convert Numpy array to tensor
        Ob = paddle.to_tensor(Observable(self.n))
        label_pp = reshape(paddle.to_tensor(label), [-1, 1])

        # Build the quantum circuit
        Utheta = self.circuit.unitary_matrix()

        # Because Utheta is achieved by learning, we compute with row vectors to speed up without affecting the training effect
        state_out = matmul(state_in, Utheta)  # shape:[-1, 1, 2 ** n], the first parameter is BATCH in this tutorial

        # Measure the expectation value of Pauli Z operator <Z> -- shape [-1,1,1]
        E_Z = matmul(matmul(state_out, Ob), transpose(paddle.conj(state_out), perm=[0, 2, 1]))

        # Mapping <Z> to the estimated value of the label
        state_predict = paddle.real(E_Z)[:, 0] * 0.5 + 0.5 + self.bias  # |y^{i,k} - \tilde{y}^{i,k}|^2
        loss = paddle.mean((state_predict - label_pp) ** 2)  # Get average for "BATCH" |y^{i,k} - \tilde{y}^{i,k}|^2: L_i：shape:[1,1]

        # Calculate the accuracy of cross-validation
        is_correct = (paddle.abs(state_predict - label_pp) < 0.5).nonzero().shape[0]
        acc = is_correct / label.shape[0]

        return loss, acc, state_predict.numpy(), self.circuit

Training Process

# Draw the figure of the final training classifier
def heatmap_plot(Opt_Classifier, N):
    # generate data points x_y_
    Num_points = 30
    x_y_ = []
    for row_y in np.linspace(0.9, -0.9, Num_points):
        row = []
        for row_x in np.linspace(-0.9, 0.9, Num_points):
            row.append([row_x, row_y])
        x_y_.append(row)
    x_y_ = np.array(x_y_).reshape(-1, 2).astype("float64")

    # make prediction: heat_data
    input_state_test = paddle.to_tensor(
        datapoints_transform_to_state(x_y_, N))
    loss_useless, acc_useless, state_predict, cir = Opt_Classifier(state_in=input_state_test, label=x_y_[:, 0])
    heat_data = state_predict.reshape(Num_points, Num_points)

    # plot
    fig = plt.figure(1)
    ax = fig.add_subplot(111)
    x_label = np.linspace(-0.9, 0.9, 3)
    y_label = np.linspace(0.9, -0.9, 3)
    ax.set_xticks([0, Num_points // 2, Num_points - 1])
    ax.set_xticklabels(x_label)
    ax.set_yticks([0, Num_points // 2, Num_points - 1])
    ax.set_yticklabels(y_label)
    im = ax.imshow(heat_data, cmap=plt.cm.RdBu)
    plt.colorbar(im)
    plt.show()

# Learn the PQC via Adam

def QClassifier(Ntrain, Ntest, gap, N, DEPTH, EPOCH, LR, BATCH, seed_paras, seed_data):
    """
    Quantum Binary Classifier
    Input:
        Ntrain         # Specify the training set size
        Ntest          # Specify the test set size
        gap            # Set the width of the decision boundary
        N              # Number of qubits required
        DEPTH          # Circuit depth
        BATCH          # Batch size during training
        EPOCH          # Number of training epochs, the total iteration number "EPOCH * (Ntrain / BATCH)" is chosen to be about 200
        LR             # Set the learning rate
        seed_paras     # Set random seed to initialize various parameters
        seed_data      # Fixed random seed required to generate the data set
        plot_heat_map  # Whether to plot heat map, default True
    """
    # Generate data set
    train_x, train_y, test_x, test_y = circle_data_point_generator(Ntrain=Ntrain, Ntest=Ntest, boundary_gap=gap, seed_data=seed_data)
    # Read the dimension of the training set
    N_train = train_x.shape[0]
    
    paddle.seed(seed_paras)
    # Initialize the registers to store the accuracy rate and other information
    summary_iter, summary_test_acc = [], []

    # Generally, we use Adam optimizer to get relatively good convergence
    # Of course, it can be changed to SGD or RMSprop
    myLayer = Opt_Classifier(n=N, depth=DEPTH)  # Initial PQC
    opt = paddle.optimizer.Adam(learning_rate=LR, parameters=myLayer.parameters())


    # Optimize iteration
    # We divide the training set into "Ntrain/BATCH" groups
    # For each group the final circuit will be used as the initial circuit for the next group
    # Use cir to record the final circuit after learning.
    i = 0  # Record the iteration number
    for ep in range(EPOCH):
        # Learn for each group
        for itr in range(N_train // BATCH):
            i += 1  # Record the iteration number
            # Encode classical data into a quantum state |psi>, dimension [BATCH, 2 ** N]
            input_state = paddle.to_tensor(datapoints_transform_to_state(train_x[itr * BATCH:(itr + 1) * BATCH], N))

            # Run forward propagation to calculate loss function
            loss, train_acc, state_predict_useless, cir \
                = myLayer(state_in=input_state, label=train_y[itr * BATCH:(itr + 1) * BATCH])  # optimize the given PQC
            # Print the performance in iteration
            if i % 30 == 5:
                # Calculate the correct rate on the test set test_acc
                input_state_test = paddle.to_tensor(datapoints_transform_to_state(test_x, N))
                loss_useless, test_acc, state_predict_useless, t_cir \
                    = myLayer(state_in=input_state_test,label=test_y)
                print("epoch:", ep, "iter:", itr,
                      "loss: %.4f" % loss.numpy(),
                      "train acc: %.4f" % train_acc,
                      "test acc: %.4f" % test_acc)
                # Store accuracy rate and other information
                summary_iter.append(itr + ep * N_train)
                summary_test_acc.append(test_acc) 

            # Run back propagation to minimize the loss function
            loss.backward()
            opt.minimize(loss)
            opt.clear_grad()
            
    # Print the final circuit
    print("The trained circuit:")
    print(cir)
    # Draw the decision boundary represented by heatmap
    heatmap_plot(myLayer, N=N)

    return summary_test_acc

def main():
    """
    main
    """
    time_start = time.time()
    acc = QClassifier(
        Ntrain = 200,    # Specify the training set size
        Ntest = 100,     # Specify the test set size
        gap = 0.5,       # Set the width of the decision boundary
        N = 4,           # Number of qubits required
        DEPTH = 1,       # Circuit depth
        BATCH = 20,      # Batch size during training
        EPOCH = int(200 * BATCH / Ntrain),
                        # Number of training epochs, the total iteration number "EPOCH * (Ntrain / BATCH)" is chosen to be about 200
        LR = 0.01,       # Set the learning rate
        seed_paras = 19, # Set random seed to initialize various parameters
        seed_data = 2,   # Fixed random seed required to generate the data set
    )
    
    time_span = time.time()-time_start
    print('The main program finished running in ', time_span, 'seconds.')

if __name__ == '__main__':
    main()

The dimensions of the training set x (200, 2) and y (200, 1)
The dimensions of the test set x (100, 2) and y (100, 1) 

epoch: 0 iter: 4 loss: 0.2750 train acc: 0.7000 test acc: 0.6700

epoch: 3 iter: 4 loss: 0.2471 train acc: 0.2500 test acc: 0.5500
epoch: 6 iter: 4 loss: 0.1976 train acc: 0.8000 test acc: 0.9200
epoch: 9 iter: 4 loss: 0.1639 train acc: 1.0000 test acc: 1.0000
epoch: 12 iter: 4 loss: 0.1441 train acc: 1.0000 test acc: 1.0000
epoch: 15 iter: 4 loss: 0.1337 train acc: 1.0000 test acc: 1.0000
epoch: 18 iter: 4 loss: 0.1287 train acc: 1.0000 test acc: 1.0000
The trained circuit:
--Rz(3.490)----Ry(5.436)----Rz(3.281)----*--------------x----Ry(0.098)--
                                         |              |               
--Rz(1.499)----Ry(2.579)----Rz(3.496)----x----*---------|----Ry(1.282)--
                                              |         |               
--Rz(5.956)----Ry(3.158)----Rz(3.949)---------x----*----|----Ry(1.418)--
                                                   |    |               
--Rz(1.604)----Ry(0.722)----Rz(5.037)--------------x----*----Ry(2.437)--

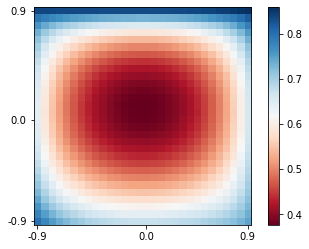
The main program finished running in  7.628719806671143 seconds.

Tổng kết

Như vậy chúng ta đã đi qua một loạt các khái niệm cơ bản về Quantum Computing và Quantum Neural Network, đồng thời xây dựng một mạng neuron lượng tử đơn giản. Theo như những nghiên cứu gần đây thì mặc dù đã có nhiều bước phát triển trong lĩnh vực học máy lượng tử thế nhưng câu hỏi liệu mạng nơ-ron lượng tử có mạnh hơn mạng nơ-ron cổ điển hay không vẫn còn bỏ ngỏ. Đây là một công nghệ khá non trẻ nhưng tiềm năng của nó lại rất lớn trong ngành trí tuệ nhân tạo. Bài viết cũng đã dài, cảm ơn các bạn dành thời gian đọc, nếu có sai sót hoặc thắc mắc các bạn có thể comment ở bên dưới và mình sẽ cố gắng giải đáp nếu trong tầm hiểu biết của mình 😅. Hẹn các bạn trong bài viết tiếp theo.

References

deeplearning Quantum Neural Network Quantum Computing

Một số kiến thức cần nắm

Đặt vấn đề

Qubit là gì?

Biểu diễn toán học

Biểu diễn bloch sphere

Cổng Logic Quantum

Cổng đơn qubit

Cổng đa qubit

Measurement

Quantum Neural Network

QClassifier

Data processing

Build Quantum Neural Network

Measurement

Loss function

Tổng kết

References

Mục lục