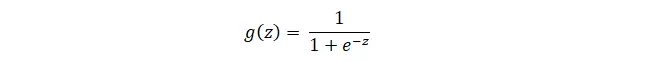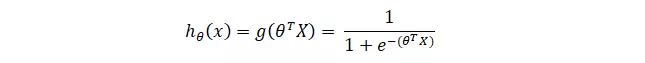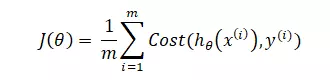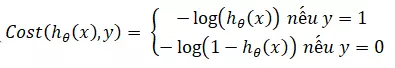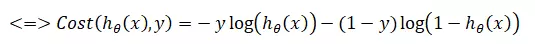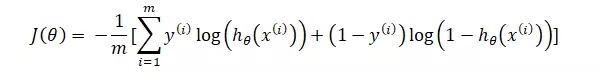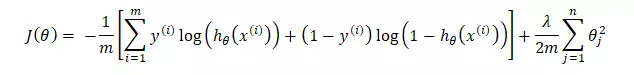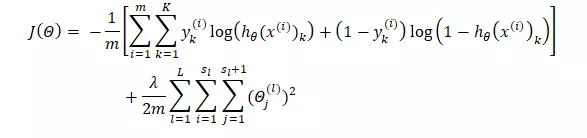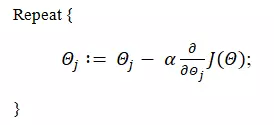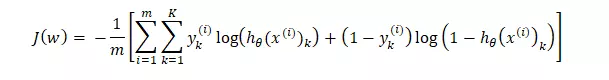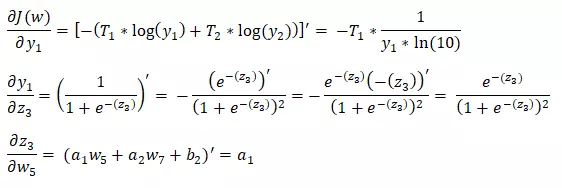SƠ LƯỢC VỀ ARTIFICIAL NEURAL NETWORK

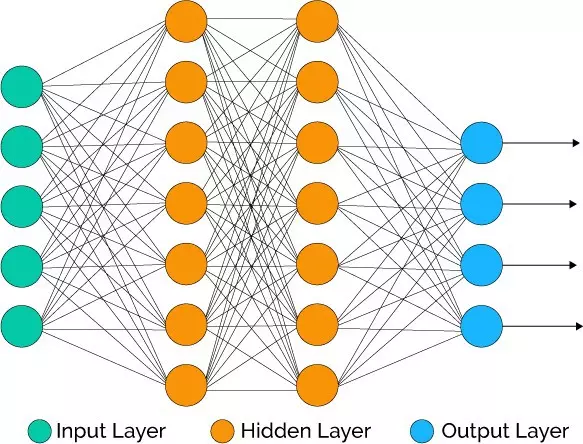
Artificial Neural Network (ANN) gồm 3 thành phần chính: Input layer và output layer chỉ gồm 1 layer , hidden layer có thể có 1 hay nhiều layer tùy vào bài toán cụ thể. ANN hoạt động theo hướng mô tả lại cách hoạt động của hệ thần kinh với các neuron được kết nối với nhau
Trong ANN, trừ input layer thì tất cả các node thuộc các layer khác đều full-connected với các node thuộc layer trước nó. Mỗi node thuộc hidden layer nhận vào ma trận đầu vào từ layer trước và kết hợp với trọng số để ra được kết quả. Ở trong course của Andrew Ng trên coursera, thầy sử dụng Logistic Regression ở các node.

Sơ qua về Logistic Regression:

Logistic Regression có activation function là hàm sigmoid :

Hàm hypothesys :

Đồ thị có dạng :

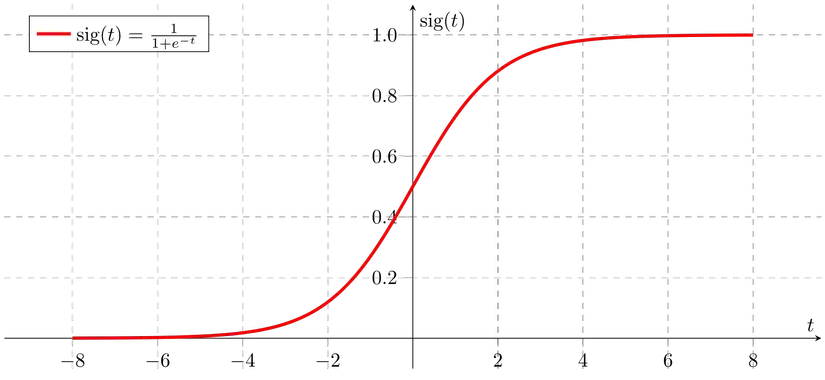
Cost function:

Với :

Vậy ta có cost function :

Kết hợp với Regurlarization:

Vậy với ANN với mỗi node thuộc layer khác input layer đều là một Logistic Regression ta sẽ có :

Công việc của chúng ta hiện tại là tìm ra được $\Theta$ sao cho $J(\Theta)$ min.
Để tìm cực tiểu của $J(\Theta)$ ta áp dụng thuật toán Gradient Descent.

Với α là learning rate.
Để thực hiện được thì cần phải tính được $\frac{∂}{∂\Theta_{j}}J(\Theta)$, để tính được đạo hàm này là việc tương đối khó và ta cần thực hiện một thuật toán được gọi là backpropagation để tính.

FORWARD PROPAGATION

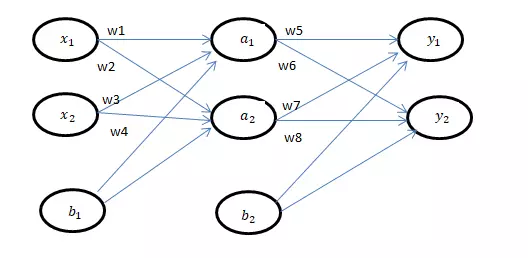
Ta có mạng neural như sau :

Chú thích :
$x_{1},x_{2}$ là các features của input.
$y_{1},y_{2}$ là các output.
$b_1,b_2$ là các bias.
$w_1,w_2,…,w_8$ là các trọng số.
Như cái tên của forward propagation , ta sẽ tiến hành tính toán $a_{1},a_{2},y_{1},y_{2}$ từ trái qua phải.

$z_{1}=x_{1} w_{1}+x_{2} w_{3}+b_{1}$
$a_{1}=sigmoid(z_{1} )=\frac{1}{1+e^{x_{1} w_{1}+x_{2} w_{3}+b_{1}}}$

Tương tự :

$z_{2}=x_{1} w_{2}+ x_{2} w_{4}+b_{2}$
$a_{2}=\frac{1}{1+e^{x_{1} w_{2}+ x_{2} w_{4}+b_{2}}}$
$z_{3}=a_{1} w_{5}+a_{2} w_{7}+b_{2}$
$y_{1}=\frac{1}{1+e^{a_{1} w_{5}+a_{2} w_{7}+b_{2}}}$
$z_{4}=a_{1} w_{6}+a_{2} w_{8}+b_{2}$
$y_{2}=\frac{1}{1+e^{a_{1} w_{6}+a_{2} w_{8}+b_{2}}}$

Forward propagation là một công đoạn tính toán giá trị tại từng node để phục vụ việc tính toán trong Back propagation.

BACK PROPAGATION

Như đã nói ở trên, mục tiêu của back propagation là đi tính $\frac{∂}{∂\Theta_{j}} J(\Theta)$.
Giả sử ta đang cần tính $\frac{∂}{∂\Theta_{5}} J(\Theta)$.
Áp dụng chain rule ta tách $\frac{∂}{∂\Theta_{5}} J(\Theta)$thành :
$\frac{∂}{∂w_{5}} J(w)= \frac{∂J(w)}{∂y_1}* \frac{∂y_1}{∂z_3}* \frac{∂z_3}{∂w_5 }$
Để cho dễ hiểu chúng ta sẽ bỏ qua regularization và giả sử m = 1 với tập kết quả trong training set ứng với $y_1,y_2 $ là $T_1=1,T_2=0$ :

Tất cả các kết quả của $\frac{∂J(w)}{∂y_1},\frac{∂y_1}{∂z_3},\frac{∂z_3}{∂w_5}$ đều có thể tính được thông qua kết quả thu được từ forward propagation. Vậy ta có thể tính được $\frac{∂}{∂w_5} J(w)$.
Tương tự như vậy ta có thể lần lượt tính được giá trị $\frac{∂}{∂w_j} J(w)$ với j = 1, 2, …, 8 trong trường hợp này.
Như vậy nhờ vào back propagation ta đã có thể tính được $\frac{∂}{∂w_j} J(w)$ từ đó giúp thuật toán Gradient descent có thể hoạt động và ta có thể tìm ra tập $\Theta$ sao cho Cost function là nhỏ nhất.