Tìm hiểu về từ khoá "tailrec" trong Kotlin để viết hàm tính 1.000.000 giai thừa

Tailrec là một từ khoá được thêm vào Kotlin từ phiên bản 1.0, nó là viết tắt của cụm từ "tail recursion" - tức đệ quy đuôi. Hiểu và biết cách sử dụng từ khoá tailrec trong Kotlin sẽ giúp công việc lập trình của bạn trở nên thú vị hơn nhiều. Vì có thể có những bạn chưa biết đệ quy và đệ quy đuôi là gì nên trước hết chúng ta hãy nói sơ qua về đệ quy đã nhé.

Đệ quy là gì ?

Theo Wikipedia tiếng Việt:

Đệ quy (tiếng Anh: recursion) là phương pháp dùng trong các chương trình máy tính trong đó có một hàm tự gọi chính nó.

Một ví dụ với đệ quy đó là hàm tính giai thừa. Ta luôn biết n! = n * (n - 1)! vì vậy ta có thể viết một hàm đệ quy như sau:

fun factorial(n: Long): Long {
    return if (n == 1L) 1 else n * factorial(n - 1)
}

Đệ quy đuôi là gì ?

Ở ví dụ ở trên khi gọi factorial(5) chương trình sẽ thực hiện như sau:

factorial(5)
5 * factorial(4)
5 * (4 * factorial(3))
5 * (4 * (3 * factorial(2)))
5 * (4 * (3 * (2 * factorial(1))))
5 * (4 * (3 * (2 * 1)))
5 * (4 * (3 * 2))
5 * (4 * 6)
5 * 24
120

Ta dễ thấy rằng factorial(5) phải chờ kết quả của factorial(4) thì mới tiếp tục tính toán được, factorial(4) thì lại phải chờ kết quả của factorial(3)... Do việc gọi đệ quy được thực hiện trước việc tính toán nên đây được gọi là một hàm đệ quy đầu (head recursion). Chính vì mỗi lần gọi đệ quy lại phải lưu trạng thái hàm hiện tại vào call stack để chờ tính toán tiếp nên trong trường hợp call stack quá lớn chương trình sẽ gặp lỗi stack over flow.

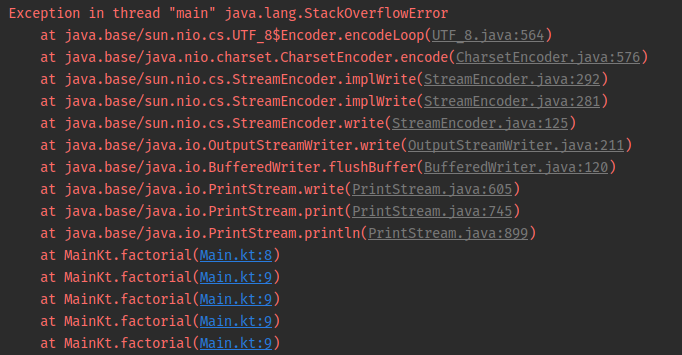
Với đệ quy đuôi (tail recursion), tất cả các phép toán sẽ được thực hiện trước khi gọi đệ quy. Hàm trên có thể viết lại bằng đệ quy đuôi như sau:

fun factorial(n: Long, a: Long = 1): Long {
    return if (n == 1L) a else factorial(n - 1, a * n)
}

Khi chạy chương trình trên với factorial(5), nó sẽ thực hiện như sau:

factorial(5, 1)
factorial(4, 5)
factorial(3, 20)
factorial(2, 60)
factorial(1, 120)
120

Do việc tính toán được xử lý dứt điểm nên khi gọi đệ quy trạng thái của hàm hiện tại không cần phải lưu vào call stack để tính toán tiếp nên sẽ hạn chế được stack over flow.

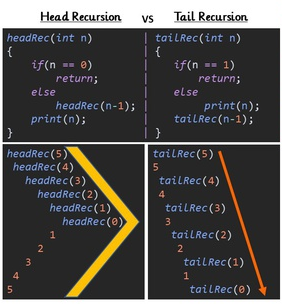
Điều này có nghĩa là đệ quy đuôi chạy một mạch từ hàm đầu tiên đến hàm cuối cùng và lấy được kết quả, trong khi đệ quy đầu phải chạy từ hàm đầu tiên đến hàm cuối cùng rồi lại quay trở về hàm đầu tiên để lấy được kết quả (xem hình minh hoạ). Chính vì vậy về bản chất, đệ quy đuôi giống như một vòng lặp và đây là lý do từ khoá tailrec trong Kotlin ra đời.

Từ khoá "tailrec" trong Kotlin là gì ?

Do là một ngôn ngữ ra đời sau và vẫn đang trong quá trình hoàn thiện nên Kotlin đã (đang và sẽ tiếp tục) học hỏi và thừa hưởng các tính năng hay ho từ các ngôn ngữ đi trước. tailrec trong Kotlin cũng được học hỏi từ annotation @tailrec của Scala. Vậy thì từ khoá tailrec của Kotlin có chức năng gì ?

Ngay cả với đệ quy đuôi, khi gọi đệ quy, một vùng nhớ mới vẫn được tạo mới để thực thi lần gọi đệ quy này, trong khi các vùng nhớ cũ vẫn chưa được giải phóng. Vì vậy số vùng nhớ được cấp phát sẽ tăng lên theo số bước gọi đệ quy. Tuy không cần lưu trạng thái của các hàm trước đó nhưng số lượng vùng nhớ bị cấp phát quá nhiều thì vẫn có thể bị stack over flow, nếu không thì cũng là vô cùng lãng phí do vùng nhớ ở các lần gọi trước đó tuy không còn cần đến nữa nhưng vẫn chưa được giải phóng ngay. Chính vì vậy, từ khoá tailrec được tạo ra giúp tận dụng lại vùng nhớ hiện có cho lần gọi đệ quy tiếp theo. Tức là ta chỉ cần duy nhất một vùng nhớ cho n lần gọi đệ quy bất kỳ.

Sao lại kỳ diệu như thế ? Thực ra ta không có sự kỳ diệu nào ở đây cả. Từ khoá tailrec trong Kotlin về bản chất cũng vẫn chỉ là một annotation thông báo với trình biên dịch rằng với các hàm được áp dụng với từ khoá này, sẽ chuyển đổi nó từ dạng đệ quy về dạng vòng lặp, tức là khi thực hiện nó chỉ chạy bên trong hàm đó mà thôi.

Theo đó, hàm đệ quy đuôi được thêm từ khoá tailrec dưới đây

tailrec fun factorial(n: Long, a: Long = 1): Long {
    return if (n == 1L) a else factorial(n - 1, a * n)
}

sau khi biên dịch sẽ trở thành đại loại như sau:

fun factorial(n: Long): Long {
    var n1 = n
    var a = 1L
    while (true) {
        if (n1 == 1L) {
            return a
        } else {
            a = a * n1
            n1 = n1 - 1
        }
    }
}

Như bạn thấy, hàm đệ quy đuôi ban đầu đã được convert hoàn toàn thành một hàm thông thường với một vòng lặp (khử đệ quy). Đồng thời khi bạn áp dụng tailrec cho một hàm không phải viết theo dạng đệ quy đuôi, trình biên dịch cũng sẽ báo lỗi, với IntelliJ và Android Studio thì sẽ có live warning luôn cho bạn.

Viết lại hàm giai thừa bằng Kotlin

Hàm dưới đây có thể tính được 1.000.000! mà không bị stack over flow bất kể số lần đệ quy là siêu siêu nhiều do đã áp dụng từ khoá tailrec. Tuy nhiên nó chạy lâu vãi nồi.

tailrec fun factorial(n: Long, a: BigInteger = BigInteger.ONE): BigInteger {
    return if (n == 1L) a else factorial(n - 1, a * n.toBigInteger())
}

Kết quả của factorial(1000_000) là

"The contents may not be greater than 70000 characters." nên các bạn tự chạy và xem thử nhé. =))

Cập nhật trong phiên bản 1.4

Theo issues KT-31540, từ phiên bản 1.4, tailrec sẽ được chỉnh sửa lại một chút vì một số case tương tự như sau:

var counter = 0
fun inc() = counter++

tailrec fun test(x: Int = 0, y: Int = inc(), z: Int = inc()) {
    println("y: $y, z: $z")
    if (x > 0) test(x - 1)
}

fun main() {
    test(1)
}

Khi ta chạy, sẽ thấy kết quả

y: 0, z: 1
y: 3, z: 2

Điều này khiến người dùng cảm thấy vô lý do đúng ra kết quả phải là như sau (khi bỏ từ khoá tailrec):

y: 0, z: 1
y: 2, z: 3

Điều này là do z = inc() đã được gọi trước y = inc() do các dev của JetBrains đã thực hiện gán từ tham số cuối trở về đầu. Trong khi đúng ra nó nên được gán từ đầu tới cuối. Vì vậy hiện tại nếu bạn gán default value cho tham số ghi nhớ giá trị của hàm tailrec là một giá trị không phải hằng, bạn sẽ nhận được một warning cho việc này.

Tổng kết

Bài viết này giới thiệu một cách tổng quan và dễ hiểu nhất về từ khoá tailrec trong Kotlin. Hy vọng sẽ có ích với các bạn trong việc lập trình với ngôn ngữ Kotlin thân yêu. Nếu có bất kỳ thắc mắc nào hãy để lại bình luận phía dưới bài viết này nhé.

Tham khảo thêm tại: https://kotlinlang.org/docs/reference/functions.html#tail-recursive-functions