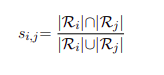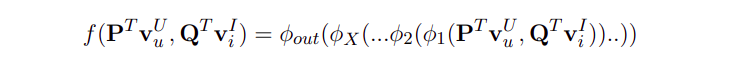Tìm hiểu phương pháp lọc cộng tác với mạng nơ-ron (NCF)

Lâu lắm rồi mình mới tìm hiểu tiếp về Hệ gợi ý ha . Chủ đề này mặc dù không liên quan trực tiếp đến công việc hiện tại của mình nhưng mình thích thì mình tìm hiểu thôi. Vì vậy nếu có gì thiếu sót thì mọi người góp ý cho mình nhé. Và chủ đề mà mình muốn chia sẻ trong bài này là phương pháp Neural Collaborative Filtering (NCF) - lọc cộng tác bằng mạng nơ-ron.

Thực ra đợt này mình cũng muốn chia sẻ nhiều thứ khác nữa cơ nhưng mà chờ Viblo MayFest nhé! Cùng cố gắng để rinh được một em áo Viblo về tủ đồ nào

Một số nhược điểm của mô hình MF

Trong bài viết về RS gần nhất thì mình đã chia sẻ về phương pháp phân rã ma trận Matrix Factorization (MF). Vì vậy, trước khi đến với NCF thì mình sẽ nói qua một chút về một số hạn chế của MF nhé:

Phương pháp MF mô hình hóa tương tác hai chiều giữa các thuộc tính ẩn của người dùng và sản phẩm. MF giả sử các chiều trong không gian ẩn đó là độc lập và tính ra giá trị tương tác bằng cách tổ hợp các chiều đó lại với cùng một trọng số. Như vậy, MF có thể coi là một mô hình tuyến tính của các thuộc tính ẩn.

Ví dụ (1):

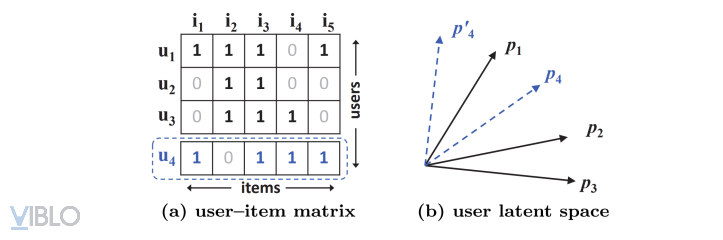
Ví dụ (1) chứng minh rằng hàm tích trong (inner product function) có thể giới hạn chất lượng của MF. Do MF chiếu người dùng và sản phẩm lên cùng một không gian ẩn, độ tương đồng giữa 2 người dùng có thể được đánh giá bằng cách sử dụng phép nhân vô hướng hoặc có thể sử dụng độ đo Cosine giữa 2 vector ẩn được tạo. Để không làm mất tính tổng quát, ta cũng có thể sử dụng độ đo Jaccard để đo độ tương tự giữa 2 người dùng trong dữ liệu ban đầu mà sau đó MF cần có khả năng nắm bắt được.

Độ đo Jaccard: Đặt $R_u$ là tập các items mà user u có tương tác, khi đó độ đo tương đồng Jaccard của hai user i và j được định nghĩa là:

Từ số liệu của ba dòng đầu tiên của hình (a) của Ví dụ (1), ta sẽ tính được $s_{2,3}$(0.66) > $s_{1,2}$(0.5) > $s_{1,3}$(0.4). Như vậy, quan hệ trên không gian của $p_1$, $p_2$, $p_3$ có thể được vẽ như trong hình (b) của ví dụ (1).

Xét user $u_4$ có $s_{4,1}$(0.6) > $s_{4,3}$(0.4) > $s_{4,2}$(0.2), điều này có nghĩa là user $u_4$ tương tự nhất với $u_1$, tiếp theo là $u_3$ và $u_2$. Tuy nhiên, do mô hình MF đưa vector người dùng lên cùng một không gian ẩn, nên với MF, có 2 cách đặt vector của user $u_4$ thỏa mãn gần $u_1$ nhất như hình vẽ trên (2 đường $p^{\prime}_4$ và $p_4$). Nhưng cả hai trường hợp này đều không thể thỏa mãn được tính chất thực tế, đó là $u_4$ gần $u_3$ hơn $u_2$. Từ đó, có thể thấy rằng MF không thể mô tả được độ đo Jaccard hay chính là độ đo sự tương tự giữa các người dùng trong trường hợp này.

Qua ví dụ trên, ta có thể thấy được MF có một số giới hạn nhất định khi cố định sử dụng một hàm tích trong (inner product) đơn giản để dự đoán cho một tương tác phức tạp giữa người dùng và sản phẩm. Một trong những cách khắc phục điều này đó là sử dụng hệ số ẩn K lớn hơn, tuy nhiên, việc này sẽ làm mất tính tổng quát của mô hình, hay chính là vấn đề overfitting, đặc biệt là trong ma trận thưa.

Phương pháp Neural Collaborative Filtering (NCF)

Do MF còn hạn chế nên việc phải thiết kế một hàm tương tác tốt hơn để mô hình hóa việc tương tác giữa các thuộc tính ẩn (latent features) của user và item là rất cần thiết. Phép toán inner product, đơn giản chỉ là việc kết hợp bằng cách nhân các thuộc tính ẩn tuyến tính, như vậy có thể không đủ để nắm bắt cấu trúc dữ liệu tương tác phức tạp của người dùng. Mô hình NCF đi khai thác phương pháp MF theo hướng này và thực hiện nó bằng mạng nơ-ron.

Mô hình NCF được nhóm tác giả Xiangnan He và cộng sự đưa ra vào năm 2017. Cấu trúc NCF tổng quát được thể hiện như trong hình vẽ:

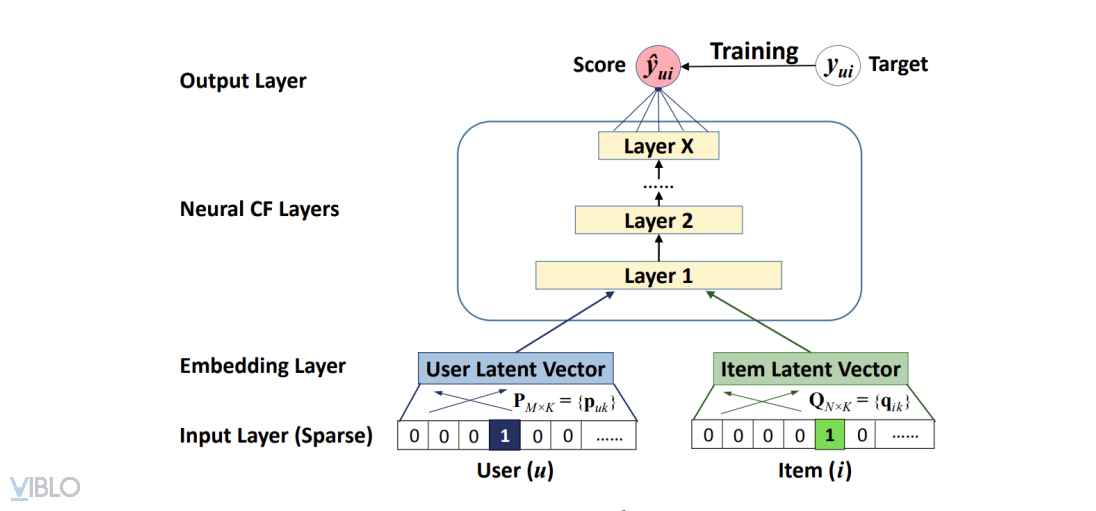
Ta có thể thấy, trong hình vẽ trên, đi từ dưới lên, mô hình NCF gồm những tầng sau:

• Tầng input: bao gồm các thuộc tính vector của user và item. Như trong hình vẽ trên, các vector đó là biểu diễn dang one-hot (vector với chỉ một trường có giá trị bằng 1, các trường còn lại có giá trị 0) dùng để biểu diễn định danh của user (userID)) và item (itemID).
• Tầng embedding: là tầng kết nối đầy đủ (fully connected) với tầng input. Qua tầng embedding, biểu diễn one-hot (dạng thưa) của user và item được biểu diễn thành vector dầy đặc (dense vector). Biểu diễn này có thể xem là biểu diễn người dùng và vật phẩm bằng các thuộc tính ẩn.
• Các tầng thuộc mạng nơ-ron (tầng 1 đến N) - Tầng neural collaborative: các tầng này có nhiệm vụ ánh xạ từ các vector embedding đến vector đầu vào của tầng output.
• Tầng output: tầng chứa điểm số dự đoán $\hat{y}_{ui}$

Việc huấn luyện NCF được thực hiện bằng cách tối thiểu hóa hàm lỗi giữa điểm số dự đoán $y^{ui}$ với giá trị mục tiêu (target) yui tương ứng.

Điểm số dự đoán được tính như sau:

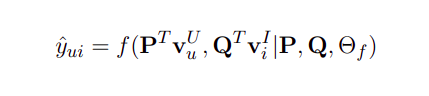
, trong đó:

• $v_u^U$, $v_i^U$ lần lượt là các ma trận hàng (vector) one-hot biểu diễn cho user u và item i.
• $P\in R^{M×K}$ và $Q \in R^{K×N}$ lần lượt là các ma trận tầng embedding chiếu $v_u^U$, $v_i^U$ vào không gian các thuộc tính ẩn. P và Q là ma trận trọng số giữa tầng input và tầng embedding.
• $\Theta_f$ là tập các tham số mô hình của hàm f. Do hàm f ở đây là ánh xạ đầu vào đầu ra của một mạng nơ-ron nên ta có thể viết f theo công thức sau: , trong đó:
• $\phi_{out}$ là hàm ánh xạ đầu vào tới đầu ra của tầng output.
• • $\phi_n, \phi_{n-1}, ..., \phi_2, \phi_1$ lần lượt là các hàm ánh xạ đầu vào tới đầu ra tại các tầng n, n-1,. . . , 2, 1 trong mạng nơ-ron.

Hàm mục tiêu NCF

Giả sử trong các tương tác người dùng và sản phẩm, ta kí hiệu Y là tập các tương tác xảy ra và quan sát được, Y− là tập các tương tác không quan sát được hay chính là các tương tác không xảy ra trong thực tế, $w_{ui}$ là hệ số của cặp học (u,i). Ta có hàm mục tiêu là hàm độ lệch bình phương giữa điểm dự đoán và điểm thực tế:

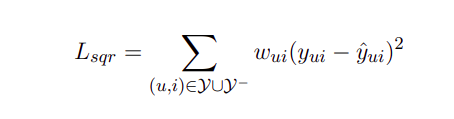
Hàm mục tiêu là hàm cực tiểu bình phương sẽ thường phù hợp cho các bài toán mà tập dữ liệu có phân phôi gần, như phân phối Gauss, mà loại phân phối này thì thường không phù hợp với dữ liệu sinh ra từ tương tác người dùng và sản phẩm. Bởi vì tương tác người dùng chỉ có thể nhận một trong 2 giá trị 0 hoặc 1, 1 nếu có xảy ra tương tác, và 0 nếu không có bất cứ tương tác nào giữa người dùng và sản phẩm. Giá trị của hàm chỉ có thế là 0 hoặc 1, chính vì vậy, ta cần một độ đo khác đặc biệt và phù hợp cho loại dữ liệu như trên.

Ta sẽ nhận được đầu ra nằm trong khoảng (0, 1) nhờ hàm activate của lớp cuối cùng. Giá trị của đầu ra thể hiện độ liên quan giữa người dùng và sản phẩm. Điểm càng cao thì độ liên quan càng cao. Để học tham số của mô hình, ta sử dụng hàm likelihood có công thức như sau:

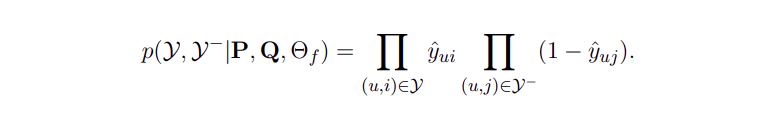
Lấy logarithm của hàm và đổi dấu, ta được:

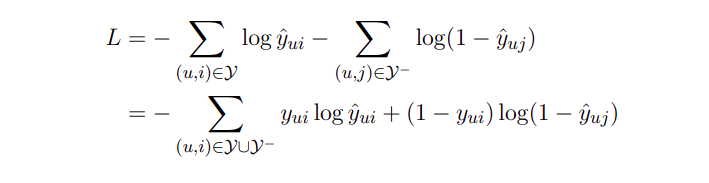
Đây chính là hàm mục tiêu của các mô hình xây dựng theo phương pháp NCF. Hàm mục tiêu này có thể được tối ưu dựa vào các phương pháp tối ưu truyền thống như SGD hay Adam. Nó tương tự như hàm mục tiêu binary cross-entropy loss (hay còn gọi là log-loss).

Tài liệu tham khảo: Neural Collaborative Filtering - Xiangnan He