Thuật toán Chia Để Trị ( Divide And Conquer ) và sắp xếp Quicksort

1.Giới thiệu

Chia để trị (Divide and conquer) là một phương pháp áp dụng cho các bài toán có thể giải quyết bằng cách chia nhỏ ra thành các bài toán con từ việc giải quyết các bài toán con này. Sau đó lời giải của các bài toán nhỏ được tổng hợp lại thành lời giải cho bài toán ban đầu. Tóm gọn lại nó gồm ba bước : Chia, trị và kết hợp

Thuật toán Quicksort là một thuật toán có đặc trưng như tên của nó đặt ra - sắp xếp nhanh. Quicksort được lựa chọn trong các cuộc thi bởi tính hiệu quả và uyển chuyển và dễ thao tác. Thuật toán có thời gian thực thi worst-case là O(n^2) ( trường hợp tồi nhất ) và hiệu quả đáng kể của nó ở mức trung bình là O(nlogn). Quicksort giống như Merge sort, áp dụng mô hình chia để trị .

2.Phân tích

Sau đây là 3 bước xử lý Quicksort cho việc sắp xếp một mảng con A[l..r] ( l - left chỉ số đầu , r - right chỉ số cuối )

Chia (Divide):

Chia mảng A[l..r] thành 2 mảng con A[l..p-1] và A[p+1..r] ( p - pivot là chỉ số chốt được lựa chọn để chia mảng, có thể là chỉ số đầu, chỉ số cuối, chỉ số trung bình hoặc ngẫu nhiên ) . Mảng con cho phép rỗng. Sao cho các phần tử bên phải pivot có giá trị lớn hơn hoặc bằng pivot cho trường hợp sắp xếp tăng dần ( ngược lại với giảm dần ) , các phàn tử bên trái pivot có giá trị nhỏ hơn hoặc bằng pivot. Tính chỉ số pivot là một phần trong bước xử lý này.

Trị (Conquer):

Sắp xếp 2 mảng con A[l...p-1] và A[p+1..r] bằng cách gọi đệ quy lại hàm trên ( Giải thuật đệ quy mình để ở link đính kèm phía dưới)

Kết hợp (Combine):

Bởi vì các mảng con đã được sắp xếp nên không cần thiết để kết hợp chúng lại nữa.

Sau đây là mô hình code tiến trình thực hiện

-Quicksort

def Quicksort(A,l,r):
    if l < r:
       p = Partition(A,l,r)
       Quicksort(A,l,p-1)
       Quicksort(A,p+1,r)

Để sắp xếp toàn bộ mảng A, ta khởi tạo hàm Quicksort(A,1,A.length)

-Partition (hàm chia)

def Partitition(A,l,r):
    pivot_value = A[r]
    i = l - 1
    for j in range(l,r):
        if A[j] <= pivot_value:
            i = i + 1
            swap(A[i],A[j])
    swap(A[i+1],A[r])
    return i+1

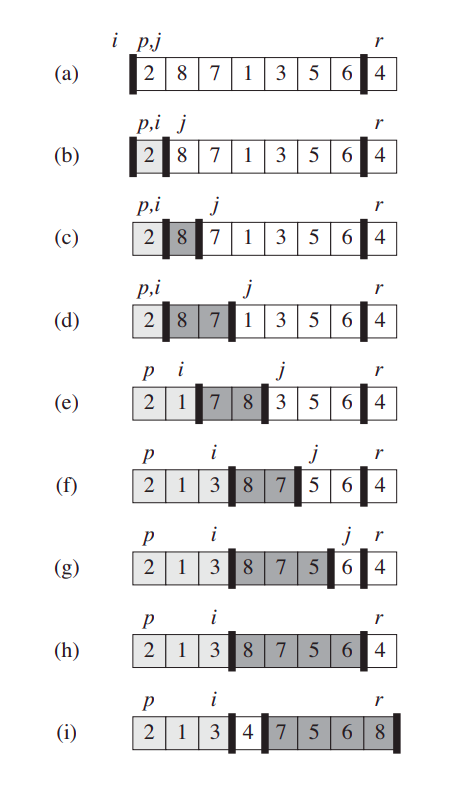
hàm Partition trên luôn lựa chọn điểm cuối mảng làm pivot ( pivot_value = A[r]) . Khi hàm chạy nó sẽ chia mảng thành 4 phần ( phần có thể không chứa phần tử nào ) . Sau mỗi lần lặp sắp xếp ta được một mảng mới có các đặc trưng sau, tại mỗi phần tử có chỉ số k bất kì thì :

1. if l <= k <= i, thì A[k] <= pivot_value
   

2. if i + 1 <= k <= j - 1, thì A[k] > pivot_value
   

3. if k = r thì A[k] = pivot_value
   

- Ví dụ minh hoạ

3.Kết luận

Như vậy chúng ta đã tìm hiểu và nắm được các bước cơ bản của giải thuật Quicksort, khi áp dụng thực tế chúng ta cần điều chỉnh các tham số đầu vào cho phù hợp với ý định của bài toán. Tuy nhiên, chỉ cần nắm được 3 bước cơ bản trên thì ta đã có thể giải quyết được hầu hết các bài toán sắp xếp. Chúc các bạn học tập tốt.

Tài Liệu tham khảo : Introduction to algorithms book