Đơn giản hoá bài toán với Kỹ thuật Chia Để Trị ( Divide And Conquer )

1.Giới thiệu

Như các bạn đã làm quen với Đệ quy, một giải thuật phổ biến. Để giải quyết một vấn đề , chúng ta gọi chúng một cách đệ quy một hoặc nhiều lần để giải quyết các vấn đề con có liên quan chặt chẽ với nhau. Thực chất, để đệ quy được một bài toán, chúng ta sẽ định hướng từ một bài toán lớn có khả năng chia thành các bài toán con mà các bài toán con có thể giải theo cách giải bài toán lớn nhưng với kích thước nhỏ hơn. Sau khi giải các bài toán con, ta kết hợp chúng lại sẽ là kết quả của bài toán lớn. Cách tiếp cận này, được gọi tên là Chia để trị ( Divide and conquer ) chúng ta cùng nhau tìm hiểu về như sau.

2. Kỹ Thuật Chia Để Trị

Lược đồ chung

Cấu trúc giải quyết bài toán gồm 3 bước :
Bước 1 - Chia ( Divide ) Chia bài toán mẹ thành các bài toán con với kích thước nhỏ hơn và có cùng cách giải quyết.
Bước 2 - Trị ( Conquer ) Trị các bài toán con lần lượt bằng cách đệ quy chúng. Chú ý chia được bài toán con càng nhỏ thì 'dạy dỗ' nó càng dễ
Bước 3 - Kết hợp ( Combine ) Kết hợp các lời giải con vào lời giải của bài toán ban đầu.

3. Vận dụng vào thuật toán Merge Sort

Lược đồ chung

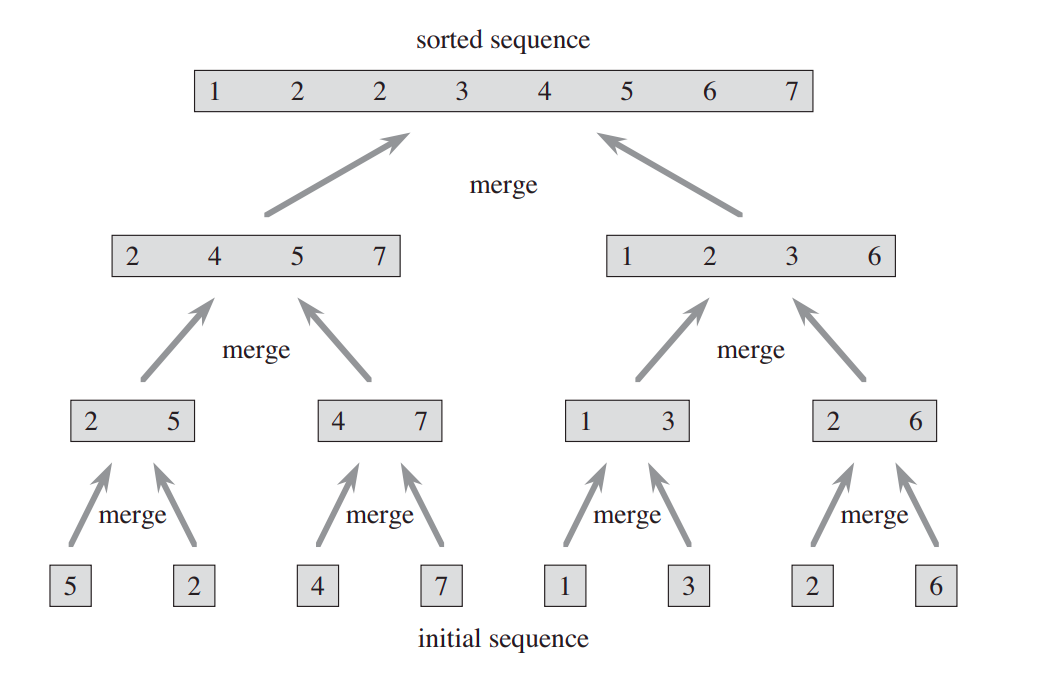
Cụ thể hoá mô hình chia để trị trên, thuật toán merge sort hay còn gọi là thuật toán sắp xếp trộn gồm có các bước :
Bước 1 : Chia mỗi chuỗi n phần tử được sắp xếp thành hai dãy con có kích thước n/2 phần tử.
Bước 2 : Sắp xếp đệ quy hai dãy con bằng cách sử dụng sắp xếp trộn
Bước 3 : Kết hợp hai chuỗi con đã sắp xếp để tạo ra chuỗi cần sắp xếp ban đầu.

• Việc đệ quy ' chạm đáy ' khi chuỗi được sắp xếp có kích thước bằng 1, trong trường hợp này không có công việc nào được thực hiện, bởi vì chuỗi có 1 phần tử thì cần gì sắp xếp nữa phải không nào ^^

• Hoạt động chính của thuật toán merge sort là trộn 2 chuỗi đã sắp xếp trong bước 2. Chúng ta trộn chúng bằng cách gọi một hàm phụ trợ Merge(A,p,q,r), trong đó A là một mảng, p , q và r là chỉ số của mảng với điều kiện p <= q < r . Ở đây, ta đã giả sử rằng 2 chuỗi con A[p..q] và A[q + 1..r] đã được sắp xếp theo đúng thứ tự. Hàm phụ trợ sẽ có nhiệm vụ trộn 2 chuỗi con này thành một chuỗi A[p..r].

• Hàm phụ trợ Merge có thời gian O(n), trong đó n = r - q + 1 là tổng số phần tử được trộn.
  Mô tả hàm Merge

   Merge(A,p,q,r)
1  n1 = q - p + 1
2  n2 = r - q
3  Khởi tạo 2 mảng rỗng mới L[1..n1+1] và R[1..n2 + 1] 
4  for i = 1 to n1
5     L[i] = A[p + i - 1]
6  for j = 1 to n2
7     R[j] = A[q + j]
8  L[n1 + 1] = vô cùng
9  R[n2 + 1] = vô cùng
10 i = 1
11 j = 1
12 for k = p to r
13     if L[i] <= R[j]
14         A[k] = L[i]
15         i = i + 1
16     else A[k] = R[j]
17         j = j + 1

Giải thích cụ thể, hàm trên sẽ thực hiện như sau: Dòng 1 tính độ dài của chuỗi con A[p..q], và dòng 2 tính độ dài của chuỗi con A[q+1..r]. Chúng ta tạo 2 mảng L và R ( left và right) lần lượt có kích thước là n1 + 1 và n2 + 1, phần tử cuối cùng của mảng sẽ đóng vai trò như cột mốc đánh dấu. Chúng ta copy mảng A[p..q] vào L[1..n1] và A[q+1..r] vào R[1..n2] như dòng 4 đến 7. Dòng 8 và 9 đặt giá trị cột mốc đánh dấu cho sự kết thúc của mảng L và R. Dòng 10-17 được minh hoạ thông qua ví dụ Merge(A,9,12,16): Giải thích : Mảng con A[9..16] chứa chuỗi < 2,4,5,7,1,2,3,6 >. Sau đó được copy vào 2 mảng chia và chèn cột mốc ( vô cùng ) như hình (a) . Ô phần tử in đậm thể hiện phần tử chưa được copy trở lại vào mảng A ( dòng 12-17) Khi được copy từ L hoặc R vào A thì ô đó được tô nhạt. Làm tương tự với các hình b , c , d ta thấy rằng, một khi chỉ số i hoặc j của mảng L và R chạm tới cột mốc ( vô cùng ) thì mảng nào còn phần tử dư nó sẽ copy trở lại vào mảng A. Như vậy, tại mỗi vòng lặp từ 12-17, mảng con A[p..k-1] sẽ chứa ít nhất k - p phần tử đúng thứ tự.

Để thấy rằng Merge chạy trong O(n) thời gian, trong đó n = r - q + 1, quan sát rằng mỗi dòng 1-3 và 8-11 lấy một thời gian cố định ( giả sử mỗi dòng có giá trị là 1), vòng lặp for từ 4-7 lấy O(n1+n2) = O(n) và có n lần lặp của vòng for ở dòng 12-17 , mỗi dòng trong đó lấy thời gian không đổi.

Bây giờ chúng ta sẽ gán hàm hỗ trợ Merge như một tiến trình con của thuật toán sắp xếp trộn. Như sau:

  Merge_sort(A,p,r)
1 if p < r:
2    q = [(p+r)/2]
3    Merge_sort(A,p,q)
4    Merge_sort(A,q+1,r)
5    Merge(A,p,q,r)

Để sắp xếp toàn bộ chuỗi A[1..n], ta gọi hàm Merge_sort(A,1,A.length)

4. Kết luận

Vừa rồi chúng ta điểm qua các nét chính của kỹ thuật chia để trị và thuật toán sắp xếp trộn. Mọi thắc mắc xin vui lòng để lại bình luận phía dưới. Chúc các bạn học tập tốt.

5. Tài liệu tham khảo

Book : Introduction to algorithm
Web : geekforgeek