TẠI SAO LẠI SỬ DỤNG ACTIVATION FUNCTION TRONG NEURAL NETWORK

Khi mọi người làm việc với mạng neural thì chắc hẳn thành phần activation function chắc hẳn không còn xa lạ gì nữa với những hàm kích hoạt như Sigmoid, Relu, softmax,.. Nhưng tại sao nó lại cần ở trong mạng Neural network. Hôm nay mình sẽ trình bày những lý do mình cho là cơ bản nhất tại sao nó được sử dụng trong mang Neural network.

1. Mạng neural network hoạt động như thế nào.

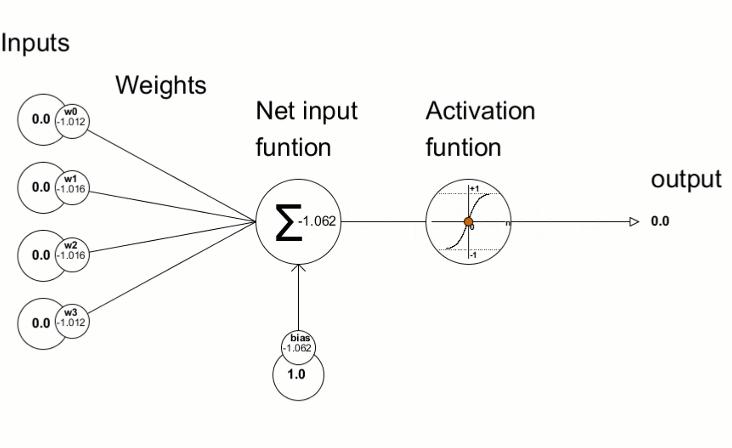
Trước khi đi vào phần giải thích thì mình sẽ qua một chút về cách mà mạng neural hoạt động. Mạng neural network sẽ lấy đầu ra của các layer phía trước sau đó nhân với các trọng số (weight) và tính tổng rồi công thêm bias và cuối cùng là đưa qua activation function để tạo ra đầu ra cho các layer hiện tại và đầu ra của một layer hiện tại sẽ tiếp tục làm đầu vào cho layer tiếp theo, như hình gif minh họa phía dưới. Từ đó giúp mạng có thể học được những biển diễn phức tạp của data. Công thức tính ouput của một layer khi nhận input từ layer phía trước là:

$A^{l}=activation(W^lA^{l-1}+B^l)$

2. Tại sao sử activation function lại cần thiết.

2.1 Tạo sự phi tuyến cho mô hình.

Như các bạn đã biết thì một bài toán đơn giản trong học máy là linear regression ở đó sử dụng một đường thẳng hoặc một siêu phẳng để biểu diễn mô hình nhưng thực tế thì data sẽ có phân bố phức tạp và sử dụng một hàm tuyến tính là không đủ mạnh để có thể biểu diễn. Như hình trên bạn có thể thấy rằng việc sử dụng một hàm tuyến tính không cho một biểu diễn tốt như hàm bậc hai. Và đối với những vấn đề lớp khác như xử lý ngôn ngữ tự nhiên, computer vision thì việc sử dụng một hàm tuyến tính để mô hình hóa là gần như không thể và ta cần phải mô hình hóa bằng sự phi tuyến. Xét một mô hình với n layer và ta giả sử tất cả các layer là tuyến tính (ko sử dụng activation function). Khi đó đầu ra của layer thứ l sẽ là:

$A^l=W^lA^{l-1}+B^l=W^l(W^{l-1}A^{l-2}+B^{l-1})+B^{l}=W^lW^{l-1}A^{l-2}+W^lB^{l-1}+B^{l}=W_dA^{l-2}+B_d$

Từ công thức trên bạn có thể thấy được rằng nếu giữa các layer đơn giản chỉ là tuyến tính thì khi đó cho dù một mô hình rất sâu đi chăng nữa thì nó thực chất vẫn là không có hidden layer và những gì bạn train nó chỉ làm tốn thời gian mà model không học được những gì đặc biệt 😂.

2.2 Giữ các giá trị output trong khoảng nhất định.

Giả sử chúng ta không sử dụng activation function và với một model với hàng triệu tham số thì kết quả của phép nhân tuyến tính từ phương trình (1) sẽ có thể là một giá trị rất lớn (dương vô cùng) hoặc rất bé (âm vô cùng) và có thể gây ra những vấn đề về mặt tính toán (nan) và mạng rất khó để có thể hội tụ. Việc sử dụng activation có thể giới hạn đầu ra ở một khoảng giá trị nào đó, ví dụ như hàm sigmoid, softmax giới hạn giá trị đầu ra trong khoảng (0, 1) cho dù kết quả của phép nhân tuyến tính là bao nhiêu đi chăng nữa.

3. Một số hàm activation function

3.1 Sigmoid

Nếu bạn tìm hiểu về machine learing thì bạn không còn xa lạ gì với hàm sigmoid trong bài toán hồi quy logic. Hàm sigmoid có dạng đường cong "S" khá đẹp. Đây là một hàm liên tục, khả vi và bị chặn trong khoảng (0, 1). Công thức của hàm sigmoid như sau:

$f(x)=\frac{1}{1+e^{-x}}$

Đây là một hàm được ưa chuộng trong quá khứ với đặc điểm có tính đạo hàm tại mọi điểm nhưng hiện nay nó ít được sử dụng hơn do một số lí do như giá trị đạo hàm của nó bị chặn trong khoảng (0, 0.25) do đó nó dễ gây hiện tượng vanishing gradient. Ngoài ra việc sử dụng hàm mũ khiến cho việc tính toán trở nên lâu hơn. Nói chung hàm sigmoid thường được sử dụng trong các bài toán hồi quy logic hoặc sử dụng trong các cơ chế attention như CBAM, SEblock,...

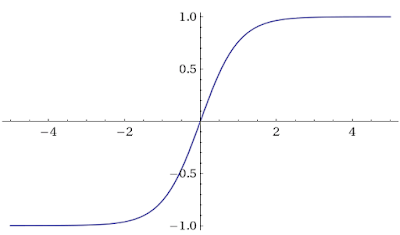
3.2 Tanh

Hàm tanh thì có hình dáng tương tự như hàm sigmoid nhưng nó khác với hàm sigmoid là nó có tính đối xứng qua gốc tọa độ và cũng có các tính chất tương tự như hàm sigmoid. Công thức của hàm Tanh như sau:

$f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$

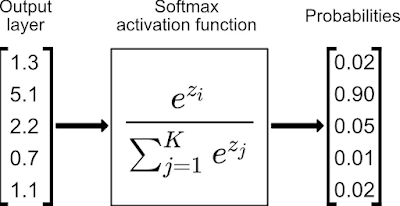
3.3 Softmax

Đây là một hàm activation thường được sử dụng ở layer cuối cùng của bài classification. Ở đó đầu ra sẽ là xác suất dự đoán rơi vào các class. Công thức hàm softmax như sau:

$f_i(z)=\frac{e^{z_i}}{\sum_{j=1}^{C}e^{z_j}}$

3.4 ReLu

Đây là một hàm activation rất được ưa chuộng sử dụng. Công thức hàm Relu như sau:

$f(x)=\max(0, x)$

Ưu điểm của hàm Relu là tính đơn giản của nó và nó đã được chứng minh là giúp tăng tốc quá trình training. Tiếp theo là nó không bị chặn như hàm sigmoid hay Tanh nên nó không phải là nguyên nhân gây ra hiện tượng vanishing gradient. Mặc dù vậy thì tại những điểm có giá trị âm thì giá trị của Relu sẽ bằng 0 (dying relu) và theo lý thuyết nó sẽ không có đạo hàm tại các điểm 0 nhưng thực tế thì người ta thường bổ sung thêm đạo hàm của relu tại 0 bằng 0 và bằng thực nghiệm người ta cũng thấy rằng xác suất để input relu rơi vào điểm 0 là rất nhỏ. Và do nó ko được chặn trên nên cũng có một nhược điểm là gây ra hiện tượng exploding gradient nhưng thường sẽ relu sẽ hoạt động tốt trong thực tế.

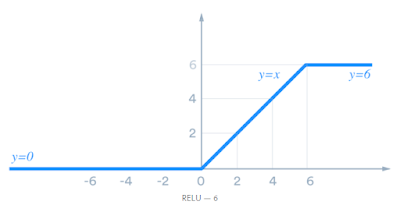
3.5 ReLu6

Như đã nói phần trên thì ReLu do không bị chặn trên nên có thể gây ra hiện tượng exploding gradient vì vậy ReLu6 đã giới hạn bên trên của hàm relu là 6 đối với input > 6. Các tính chất khác tương tự hàm ReLu như đã trình bày phía trên. Công thức hàm ReLu6 như sau:

$f(x)=\min(\max(0,x),6)$

3.6 LeakyRelu

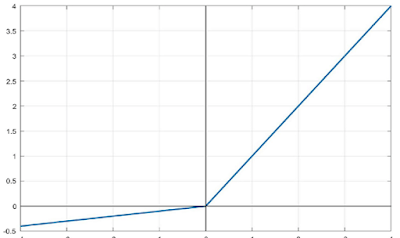
Như đã nói bên trên thì Relu có một nhược điểm là nếu input < 0 thì ouput của relu sẽ bằng 0 (dying relu) dẫn đến một số node tèo ngay lập tức và không học được gì trong quá trình training cả. Do vậy leakyRelu đã khăc phục nhược điểm trên bằng cách sử dụng một siêu tham số alpha. Công thức hàm leakyRelu như sau:

$f(x)=\max(\alpha x, x)$

Từ công thức trên ta thấy rằng alpha bằng 1 thì nó trở thành hàm kích hoạt tuyến tính và như đã thảo luận phía trên thì hàm kích hoạt tuyến tính sẽ thường không được sử dụng. Mặc định alpha thường bằng 0.01 nhưng bạn hoàn toàn có thể đặt cho alpha những giá trị mà bạn muốn.