Selection Sort
Bài đăng này đã không được cập nhật trong 2 năm
Đây là bài viết đầu tiên trong series về các thuật toán sắp xếp và tìm kiếm căn bản của mình.
Tại bài viết này, mình xin giới thiệu các bạn thuật toán sắp xếp Selection Sort.
Mình sẽ cố trình bày mọi thứ theo cách dễ hiểu nhất nhé.
Có một câu nói của Einstein dưới đây, khiến mình thực sự tâm đắc:
"Nếu bạn không giúp được một đứa trẻ 6 tuổi hiểu ra vấn đề, thị thật ra... bạn chẳng hiểu gì cả!" - Einstein
Nên nếu bạn không hiểu, thì đó là lỗi của mình nhé. Mình khuyến khích các bạn hỏi tất cả mọi thứ mà bản thân thắc mắc luôn ha.
Vậy nhé, mình bắt đầu nè...
Vấn đề đặt ra
Nếu ai đó cho bạn một dãy số gồm N phần tử lộn xộn, thì bạn sẽ làm như thế nào để sắp xếp tăng dần nó nhỉ?
Ý tưởng đơn giản nhất
có thể nghĩ ra là:
- Bước 1. Đầu tiên, mình sẽ tìm ra giá trị nhỏ nhất của dãy số từ vị trí 1..N.
- Bước 2. Sau đó, đổi chỗ giá trị nhỏ nhất đó cho vị trí đầu tiên của dãy.
- Bước 3. Lặp lại bước 1 và bước 2, nhưng là từ vị trí số 2 (vì giờ đây ta đã có giá trị đầu tiên là giá trị nhỏ nhất rồi, nên có thể bỏ qua nó).
Nhận xét: Mình để ý rằng, khi đến bước 3, thực sự ta đã thu hẹp được bài toán. Từ dãy số 1..N, giờ đây chỉ còn 2..N. Và cứ như thế thì ta cứ thu hẹp dần cho đến N..N thì coi như xong. Và đây chính là thuật toán selection sort.
Trên một số tài liệu có thể code sẽ khác, nhưng nhìn chung vẫn là ý tưởng đó nhưng lại diễn giải theo một cách khác mà thành.
Dưới đây là hình minh họa cho thuật toán này (nguồn ảnh):
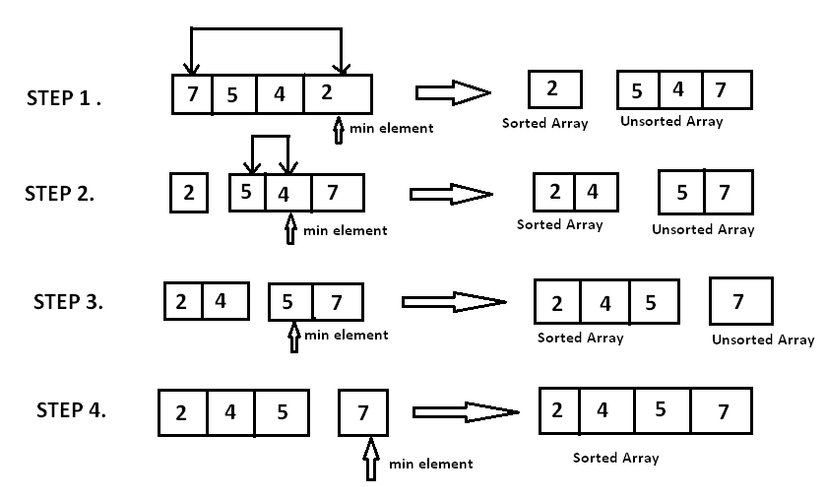
Dưới đây là đoạn code mẫu mình đã chuẩn bị:
for (int i=0; i<n-1; i++) {
// Tìm vị trí giá trị nhỏ nhất trong đoạn từ i..n
int minPosition = i;
for (int j=i+1; j<n; j++) {
if (arr[minPosition] > arr[j]) {
minPosition = j;
}
}
// Đổi chổ giá trị nhỏ nhất đó cho arr[i]
swap(arr[i], arr[minPosition]);
}
Full chương trình bạn có thể xem ở đây: https://ideone.com/YGIeFC
Độ phức tạp
của thuật toán này là:
(Nếu bạn chưa biết cách để xác định độ phức tạp của một thuật toán thì mình có thể nói sơ qua là: số lượng phép gán và so sánh được dùng để xây dựng thuật toán. Nếu các bạn muốn tìm hiểu thêm, xin hãy để lại comment, để mình có thể viết bài về cách đánh giá độ phức tạp của thuật toán này).
Ứng dụng
Như ta đã thấy ở trên, độ phức tạp thuật toán là:
Ta có thể hình dung: Máy tính đời nay có thể xử lý tầm phép tính/giây, thì thời gian để sắp xếp dãy số kích thước N là: (s).
Dưới đây là bảng ví dụ về thời gian chạy của thuật toán này:
| N | Time |
|---|---|
| 100 | 0,00(s) |
| 10.000 | 0,10(s) |
| 1.000.000 | 1.000(s) |
| 100.000.000 | 10.000.000(s) |
Với độ phức tạp cao như vậy thì lúc nào ta nên sử dụng nó?
- Khi bạn cần sắp xếp một dãy các phần tử có kích thước nhỏ (tầm 50-100 phần tử) thì đây là một thuật toán dễ hiểu, dễ implement.
- Khi bạn chỉ cần lấy K số nhỏ nhất (hoặc lớn nhất) đầu tiên của dãy. Nếu bạn chỉ cần lấy K phần tử nhỏ nhất đầu tiên của dãy (với K và N nhỏ) mà lại dùng đến các thuật toán to bự như: QuickSort thì thật là không nên.
All rights reserved