Quick Sort

Chào các bạn!
Tiếp theo chuỗi series về các thuật toán sắp xếp và tìm kiếm căn bản, thì ở bài viết này mình sẽ trình bày các bạn phần thuật toán Sắp xếp nhanh - Quick Sort.
Được mệnh danh là một trong các thuật toán sắp xếp nhanh, hiệu quả và dễ implement! Chúng ta cùng tìm hiểu xem nó sao nhé!

Đặt vấn đề

Cho một dãy số kích thước N phần tử, hãy sắp xếp dãy số đó theo thứ tự tăng dần.

Ở bài viết trước, mình đã trình bày về giải thuật Selection Sort, thì ta đã thấy rằng, nhược điểm của nó là... quá chậm. Và trong một số ứng dụng, điều này là không thể chấp nhận.
Vậy nên từ đó, người ta đã nghĩ ra một giải pháp chạy nhanh hơn, thay thế cho Selection Sort với độ phức tạp thuật toán nhỏ hơn - $O(n*logn)$ (tuy nhiên, không phải lúc nào cũng đúng bằng $n*logn$ nhé mn).

Ý tưởng thuật toán

Thuật toán chia làm 3 bước sau đây:

Nếu dãy số đã cho có không quá 1 phần tử, thì coi như dãy số đã được sắp xếp. Không cần làm gì thêm.
Trong trường hợp dãy số nhiều hơn 1 phần tử thì, chia dãy số đã cho ra làm 2 nửa:
- Nửa bên trái bao gồm các số $\lt X$
- Nửa bên phải bao gồm các số $\geq X$
với $X$ là một giá trị nào đó (thuộc dãy số đã cho).
Tiếp tục, lặp lại bước 1, bước 2 ở trên với 2 dãy con vừa chia đôi một cách độc lập.

Dưới đây là hình minh họa cho thuật toán này (nguồn ảnh)

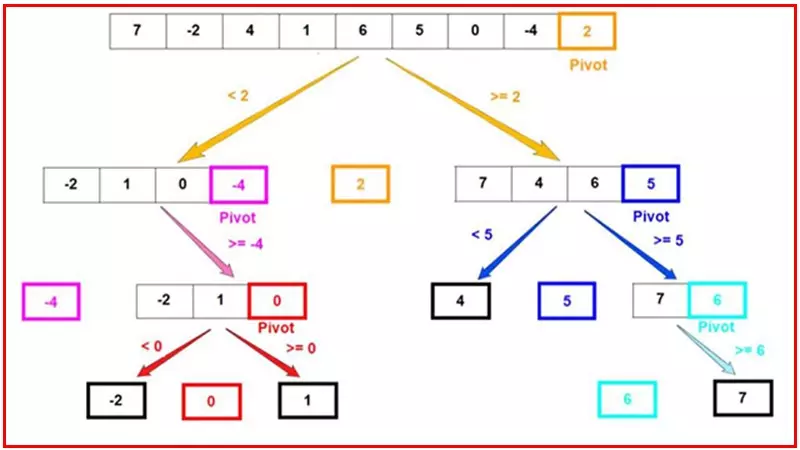
Có 2 điểm quan trọng nhất của thuật toán này mà bạn cần nắm chắc. Chỉ cần nắm chắc nó, thì coi như bạn đã hiểu rõ thuật toán QuickSort, để rồi không cần phải học thuộc hay copy code gì nữa... 2 điểm đó là:

Ý tưởng chính của thuật toán là: chia để trị (chia dãy số ra làm 2)
Nhưng chia như thế nào? Cách chọn giá trị $X$ là điểm mấu chốt

Dưới đây là đoạn code mẫu mình đã chuẩn bị:


void quickSort(int *arr, int l, int r) {
    // Nếu dãy số không quá 1 phần tử
    if (l >= r) return;

    // Nếu dãy số >1 phần tử
    int i = l, j = r;
    // Chọn X là giá trị ngẫu nhiên trong arr
    int X = arr[random(l, r)];
    
    // Phân đôi dãy số
    while (i < j) {
        while (arr[i] < X) i++;
        while (arr[j] > X) j--;
        if (i <= j) swap(arr[i++], arr[j--]);
    }
    // Sau vòng lặp while ở trên, ta đã có: 
    // [l..j] bao gôm những giá trị <= X
    // [i..r] bao gồm những giá trị >= X
    // Tuy nhiên, không đảm bảo rằng các phần tử trong 2 dãy con này đã được sắp xếp.
    // Do đó, ta cần gọi lại đệ quy để xử lý 2 dãy con.
    quickSort(arr, i, r);
    quickSort(arr, l, j);
}

Xem full code chương trình: https://ideone.com/hI4NQB

Đoạn code trên, mình đã lựa chọn điểm $X$ chính là giá trị ngẫu nhiên trong dãy số. Lí do vì sao thì là để cho dãy số được chia 2 dựa trên một yếu tố ngẫu nhiên (lưu ý: một số tài liệu khác có thể chọn giá trị cố định như ở đầu hoặc ở cuối hoặc giữa). Và điều này, theo mình là hoàn toàn không liên quan đến tốc độ chạy của thuật toán, do dãy số đã cho ban đầu cũng sẽ có một thứ tự ngẫu nhiên không biết trước được, dẫn đến cách chọn nào cũng sẽ có ưu và nhược điểm. Nhưng ở đây, mình vẫn lựa chọn vị trí ngẫu nhiên, để ý muốn nói rằng, chúng ta hoàn toàn tự do trong việc lựa chọn giá trị $X$ .

Đánh giá độ phức tạp

Độ phức tạp của thuật toán Quick sort đã được chứng minh đạt giá trị trung bình là: $O(N*logN)$ . Khi các bạn nhấm vào link full code ở trên: các bạn sẽ tìm thấy dòng

Success #stdin #stdout 0.14s 7508KB

Nó mô tả Memory và Thời gian xử lý của đoạn code: mình đã tạo ra ngẫu nhiên 1.000.000 số và sắp xếp lại nó, nhưng thời gian sắp xếp chỉ có 0.14s. Cho thấy độ mạnh mẽ của thuật toán.

Kết luận

Trên đây, mình đã trình bày các bạn về thuật toán Quick Sort. Hi vọng bài viết sẽ giúp bạn phần nào hiểu được ý tưởng cũng như cài đặt nó mà không cần học thuộc bất cứ dòng code nào.

Nếu bạn có bất cứ ý kiến nào đóng góp, xin hãy gửi comment, mình sẽ trả lời và khắc phục cho những lần sau.

Đặt vấn đề

Ý tưởng thuật toán

Đánh giá độ phức tạp

Kết luận

Mục lục