7.4K 447 29

Đã đăng vào thg 12 14, 2017 11:55 SA 12 phút đọc

55.4K

Random() có thực sự ngẫu nhiên ?

Bài đăng này đã không được cập nhật trong 5 năm

Không, trên đời chẳng có gì là ngẫu nhiên cả!

Tất cả đều là những quy luật được ẩn giấu, chỉ là chúng ta có phát hiện hay hiểu được nó hay không mà thôi; bởi đôi khi nó đơn giản, đôi khi phức tạp, thậm chí siêu phức tạp.

Random() cũng vậy. Bản thân máy tính do con người tạo ra, nên những quy tắc hoạt động của nó đều dựa trên những gì mà con người thiết kế. Tuỳ vào các hệ thống khác nhau mà random sẽ được thiết kế với các thuật toán khác nhau, nhưng ít nhất cần đảm bảo được các tiêu chí sau:

Tính ngẫu nhiên của kết quả tạo ra
Tính bảo mật của thuật toán

Quá trình sinh ra random trong máy tính được gọi là Pseudo Random Number Generation (PRNG).

1. PRNG Concept

Ta sẽ có 3 khái niệm chung trong PRNG:

Seed: giá trị khởi tạo của PRNG.
Internal State: trạng thái của PRNG, lưu trữ các biến số để có thể dự đoán được giá trị và trạng thái tiếp theo của PRNG.
Period: chu kỳ của random, random sẽ lặp lại mỗi khi chu kỳ kết thúc.

2. Random Distribution Types

Tuỳ vào mục đích sử dụng, Random() trong các ngôn ngữ lập trình sẽ sinh ra các số ngẫu nhiên theo các phân phối khác nhau.

Thông thường nhất là phân phối đều (Uniform Distribution) với xác suất xuất hiện các số là gần như nhau, hoặc phân phối chuẩn (Normal Distribution) để sinh ra các giá trị xung quanh một giá trị nào đó.

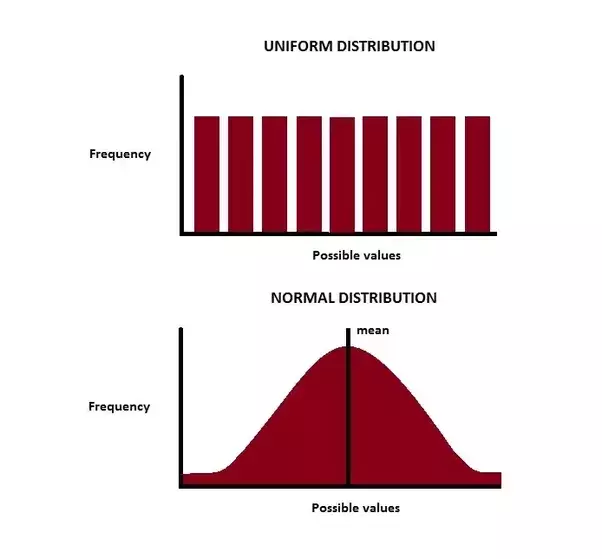
Distribution

Đó, rõ ràng Random() không phải là dùng tuỳ tiện được mà phải phụ thuộc vào việc vào chúng ta muốn dữ liệu như thế nào nữa.

3. PRNG Algorithms

Có rất nhiều thuật toán trong PRNG, các bạn có thể tham khảo thêm tại đây Trong bài này mình sẽ giới thiệu qua 3 thuật toán được sử dụng trong các ngôn ngữ lập trình.

3.1. Linear Congruential Generator (LCG)

Đây là thuật toán sinh ngẫu nhiên cổ điển nhất và phổ biến nhất được sử dụng trong PRNG. LCG là thuật toán built-in trong Pascal, C/C++, Java và C#.

LCG rất đơn giản, rất trực quan và dễ hiểu, sử dụng chỉ một hàm:

$X_{n+1} = (aX_{n} + c)\ mod\ m$

Trong đó:

$m,\ 0 < m$ : Mô đun, thường sẽ là một số đủ lớn, ví dụ $2^{32}, 2^{31} - 1, 2^{48}, 2^{64}$
$a,\ 0 < a < m$ : Hằng số nhân mutiplier
$c,\ 0 \leq c < m$ : Hằng số cộng thêm increment
$X_{0},\ 0 \leq X_{0} < m$ : seed, giá trị khởi tạo

Chu kỳ của LCG lớn nhất là m, và để LCG sinh ra tất cả các giá trị trong chu kỳ với mọi giá trị khởi tạo (full-period) thì sẽ cần những điều kiện ràng buộc như sau (các bạn hãy thử tự chứng minh bằng toán học xem sao ):

$m$ và $c$ là nguyên tố cùng nhau.
$a-1$ chia hết cho mọi thừa số nguyên tố của $m$ .
$a-1$ chia hết cho 4 nếu $m$ chia hết cho 4.

Về giá trị mặc định của các hằng số với các ngôn ngữ lập trình khác nhau, các bạn có thể tham khảo thêm tại đây.

Dưới đây là vài ví dụ về LCG:

Ưu điểm: Rất nhanh và tốn ít bộ nhớ (32 hoặc 64 bits).

Nhược điểm: Tính chất ngẫu nhiên chưa cao, và do đó với những hệ thống thực sự cần độ ngẫu nhiên rất cao, người ta không khuyến khích sử dụng LCG. Và thay vào đó là sử dụng Mersenne Twister (sẽ được nói tới trong phần sau).

3.2. Multiply with Carry (MWC)

Để tạo ra chu kỳ random lớn hơn, George Marsaglia đã đề xuất một thuật toán PRNG khác với tên gọi Multiply with Carry (MWC). Trong MWC thì ta sẽ dùng một set gồm từ hai cho tới hàng ngàn giá trị cho seed.

Và chu kỳ của MWC cũng rất lớn, từ $2^{60}$ cho tới $2^{2000000}$ , nghĩa là lớn hơn rất rất nhiều so với LCG.

Trong MWC chúng ta sẽ có một giá trị r, gọi là lag của MWC. Và cũng giống như LCG, chúng ta cũng sẽ có mutiplier và mô đun, nhưng sẽ không còn increment, mà thay vào đó là một giá trị carry. Công thức sẽ như sau:

$x_{n} = (ax_{n-r} + c_{n-1})\ \ mod \ \ b,\ n\geq r$

Trong đó, cũng giống như trên, a sẽ là mutiplier, và ở đây b sẽ là mô đun, thường là $2^{32}$ . Điểm khác biệt là giá trị carry c, giá trị này sẽ được dùng để tính toán giá trị x tiếp theo. Công thức của c là:

$c_{n} = \left\lfloor \frac{ax_{n-r} + c_{n-1}}{b} \right\rfloor,\ n\geq r$

người ta thường chọn giá trị của a sao cho $ab-1$ là Safe Prime, tức $ab-1$ và $\frac{ab}{2}-1$ đều là nguyên tố, khi đó chu kì của MWC sẽ là $\frac{ab}{2}-1$

Các bạn có thể tham khảo bảng giá trị chu kì của MWC như dưới đây:

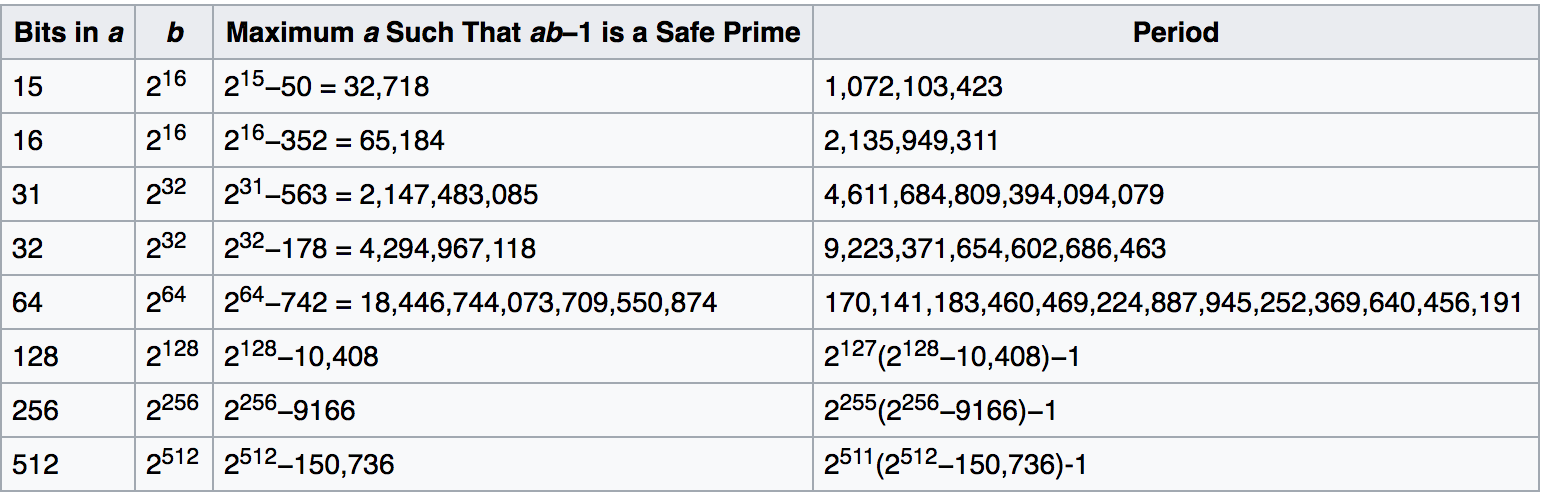
3.3 Mersenne Twister

Mersenne Twister là một thuật toán PRNG được Makoto Matsumoto và Takuji Nishimura phát triển vào năm 1997. Đây là một thuật toán thực sự tuyệt vời. Rất nhanh và tạo ra được dãy số với chất lượng ngẫu nhiên rất cao.

Mersenne Twister được sử dụng như là built-in PRNG cho Python, Ruby, PHP và R.

Cái tên Mersenne Twister được chọn vì chu kì của số ngẫu nhiên tạo ra bởi thuật toán này luôn là một số nguyên tố Mersenne

FYI: Số nguyên tố Mersenne có dạng $M_{n} = 2^{n} - 1$ , ví dụ 31.

Số nguyên tố Mersenne thường được sử dụng trong thuật toán sinh random là $2^{19937} - 1$ , đó cũng là nguồn gốc của cái tên MT19937 - standard implement của Mersene Twister. Kết quả đưa ra số tự nhiên 32 bits.

Ưu điểm:

Đưa ra được dải số rất lớn $2^{19937} - 1$
Pass rất nhiều các bài kiểm tra về tính ngẫu nhiên, có thể nói MT là một thuật toán vô cùng tốt.

Nhược điểm: MT có nhược điểm cơ bản về performance, có thể coi là chậm và tốn bộ nhớS

3.3a. Algorithm Overview

Một cách tổng quát, thuật toán Mersenne Twister được triển khai bằng đệ quy, biểu thức như sau:

$\mathbf{x_{k+n}} := \mathbf{x_{k+m}} ~~ \oplus ~~((\mathbf{x_{k}^{w-r}}~ \mid ~\mathbf{x_{k+1}^r})\mathbf{A})$

trong đó:

$w$ : word-length, độ dài của vector đầu ra x
$\mathbf{x}$ : là một vector $w$ bits, chính là đầu ra của MT
$n$ : Độ dài dãy $\mathbf{x_i}$
$r$ : điểm chia vector ra làm 2 phần, phần trái tương ứng với $w-r$ bits (upper bits), và phần phải tương ứng với $r$ bits (lower bits)
$m$ : một offset dùng cho tính toán
$A$ : ma trận vuông kích thước $w \times w$
$\mathbf{x_k^{w-r}}$ : w-r bit bên trái của $\mathbf{x_k}$
$\mathbf{x_{k+1}^r}$ : r bit bên phải của $\mathbf{x_{k+1}}$
$\mathbf{x_{k}^{w-r}}~ \mid ~\mathbf{x_{k+1}^r}$ : phép toán OR, chính là ghép w-r bit bên trái của $\mathbf{x_k}$ với r bit bên phải của $\mathbf{x_{k+1}}$ để đưa ra một vector độ dài w
$\oplus$ : phép toán XOR

Với điều kiện ràng buộc $2^{nw - r} - 1$ là số nguyên tố Mersenne.

📌 Các bạn lưu ý là mình viết vector và ma trận bằng kí tự in đậm, còn số là ký tự in thường.

Biểu thức trên chính là biểu thức Twist trong MT, mình hay gọi nó là biểu thức xoắn quẩy =))

Ma trận A được chọn lựa sao cho phép nhân ma trận trở nên đơn giản và nhanh chóng:

$\mathbf{A} = \left[\begin{matrix} 0 & 1 & 0 & \ldots & 0\\ 0 & 0 & 1 & \ldots & 0\\ \ldots & \ldots & \ldots & \ddots & \ldots \\ 0 & 0 & 0 & \ldots & 1\\ a_{w-1} & a_{w-2} & a_{w-3} & \ldots & a_{0}\\ \end{matrix} \right]$

Theo đó khi nhân một vector $\mathbf{x} = [x_{w-1}, x_{w-2},\ldots,x_{0}]$ với $A$ thì ta có thể tính toán đơn giản chỉ bằng XOR và dịch bit như sau:

$\mathbf{xA} = \left\{ \begin{matrix} \mathbf{x}~\gg~1 & x_0=0~~~ \\ (\mathbf{x}~\gg~1) \oplus \mathbf{a} & x_0=1~~~ \end{matrix} \right.$

Trong đó $\mathbf{a} = [a_{w-1}, a_{w-2},\ldots,a_{0}]$ chính là vector hàng cuối cùng của ma trận $A$ . Trông có vẻ vi diệu nhưng thực chất vẫn là nhân ma trận mà thôi, các bạn có thể khai triển thử và kiểm chứng kết quả.

Sau khi đã xây dựng được dãy các vector $\mathbf{x_0}, \mathbf{x_1}, \ldots, \mathbf{x_{n-1}}$ , để điều chỉnh phân phối của kết quả, người ta chọn một ma trận $T$ với kích thước $w \times w$ và nhân tiếp vào để ra một vector $\mathbf{z=xT}$ . Quá trình này gọi là tempering transform.

Tương tự như trên, để đơn giản hóa cho việc tính toán, người ta chọn T sao cho kết quả có thể nhận được chỉ bằng các phép XOR, AND và dịch bit thông thường

$\begin{matrix} \mathbf{y} := \mathbf{x} \oplus ((\mathbf{x} \gg u) \& \mathbf{d}) \\ \mathbf{y} := \mathbf{y} \oplus ((\mathbf{y} \ll s) \& \mathbf{b}) \\ \mathbf{y} := \mathbf{y} \oplus ((\mathbf{y} \ll t) \& \mathbf{c}) \\ \mathbf{z} := \mathbf{y} \oplus (\mathbf{y} \gg l) \end{matrix}$

trong đó:

$l, s, t, u$ : bitshift, số nguyên, thể hiện số bit dịch đi
$\mathbf{d, b, c}$ : bitmask, là các vector độ dài $w$

Và cuối cùng là đưa $w$ bit cuối cùng của $\mathbf{z}$ ra làm kết quả.

Nếu thấy hơi xoắn não, các bạn có thể xem hình bên dưới để hiểu một cách trực quan hơn cách dịch trái-phải của quá trình trên:

Initialization

Ta cần bước khởi tạo các giá trị $\mathbf{x}$ trước khi thuật toán bắt đầu. Với một giá trị đầu vào seed gán cho $\mathbf{x_0}$ .

$x_i = f \times (x_{i-1} \oplus (x_{i-1} \gg (w-2))) + i$

f là một hằng số. Với MT19937 thì $f=1812433253$

💡 Vậy là ta có cái nhìn tổng quan về Mersenne Twister, hãy ngồi xuống, nghe một ca khúc và làm một ly cà phê trước khi đến với phần code

3.3b. MT19937

MT19937 là standard implement của Mersene Twister, sử dụng với các tham số như sau:

$(w, n, m, r)$ = (32, 624, 397, 31)
$\mathbf{a}$ = $ 9908B0DF_{16} $
$(u, \mathbf{d})$ = $(11, FFFFFFFF_{16})$
$(s, \mathbf{b})$ = $(7, 9D2C5680_{16})$
$(t, \mathbf{c})$ = $(15, EFC60000_{16})$
$l$ = 18
$f$ = 1812433253

MT19937 implement code:

def _int32(x):
  # Get the 32 least significant bits.
  return int(0xFFFFFFFF & x)

class MT19937:

  def __init__(self, seed):
    # Initialize the index to 0
    self.index = 624
    self.mt = [0] * 624
    self.mt[0] = seed  # Initialize the initial state to the seed
    for i in range(1, 624):
      self.mt[i] = _int32(
        1812433253 * (self.mt[i - 1] ^ self.mt[i - 1] >> 30) + i)

  def extract_number(self):
    if self.index >= 624:
      self.twist()

    y = self.mt[self.index]

    # Right shift by 11 bits
    y = y ^ y >> 11
    # Shift y left by 7 and take the bitwise and of 2636928640
    y = y ^ y << 7 & 2636928640
    # Shift y left by 15 and take the bitwise and of y and 4022730752
    y = y ^ y << 15 & 4022730752
    # Right shift by 18 bits
    y = y ^ y >> 18

    self.index = self.index + 1

    return _int32(y)

  def twist(self):
    for i in range(624):
      # Get the most significant bit and add it to the less significant
      # bits of the next number
      y = _int32((self.mt[i] & 0x80000000) +
         (self.mt[(i + 1) % 624] & 0x7fffffff))
      self.mt[i] = self.mt[(i + 397) % 624] ^ y >> 1

      if y % 2 != 0:
        self.mt[i] = self.mt[i] ^ 0x9908b0df
    self.index = 0

a = MT19937(1000)
print a.extract_number()
print a.extract_number()
print a.extract_number()
print a.extract_number()

4. Conclusion

Vậy là rõ ràng random() không phải là ngẫu nhiên, đó đều là kết quả do máy tính (hay chính xác hơn là con người) tạo ra mà thôi.

Nếu biết được trạng thái hiện tại của thuật toán và seed, thì hoàn toàn chúng ta có thể tính toán được trạng thái tiếp theo, tức kết quả tiếp theo của random(). Tuy nhiên điều này đôi khi không dễ dàng và cần một số những điều kiện nhất định, đôi khi thấy xuất hiện trong các cuộc thi CTF.

Vậy nên, nếu bạn chưa có bạn gái, hay chưa giàu, hay chưa trúng Vietlot, hãy luôn tin rằng đó chỉ là do chưa tới lượt mà thôi, ngày ngày làm một tấm vé, dù sớm hay muộn thì may mắn cũng sẽ đến.

Good luck!