Phát hiện xâm nhập mạng bằng phát hiện bất thường dựa trên phương pháp SVM_Phần 3_Giới thiệu máy hỗ trợ véctơ SVM.

Hôm nay mình sẽ tiếp tục giới thiệu về phần máy học SVM tiếp tục với bài lần trước. Vì bài hôm nay toàn công thức toán lên khá là khó đọc mọi nguời thông cảm!!!! Nhưng nếu hiểu về tổng quát của bài toán, thì mình thấy sẽ có một cách tiếp cận với các thuật toán học máy trong môi trường mà AI đang phát triển như hiện hay. Mặc dù đc ra đời sớm nhưng mình thấy cơ chế của nó vẫn được aps dụng trong rất nhiều bài toán..

1. Tổng quan SVM.

Máy vector là một thuật toán học máy nổi tiếng được sử dụng để giải quyết bài toán phân lớp.

Thuật toán SVM ban đầu được phát minh bởi Vladimir N. Vapnik còn thuật toán SVM tiêu chuẩn hiện nay được đề xuất bởi Vladimir N. Vapnik và Corinna Cortes vào năm 1995.

SVM đã được áp dụng rất thành công trong việc giải quyết các vấn đề của thực tế xã hội như nhận dạng văn bản , nhận dạng hình ảnh, nhận dạng chữ viết tay , phân loại thư rác điện tử, phát hiện xâm nhập mạng ,...

Ban đầu bài toán SVM được viết cho bài toán phân lớp nhị phân.

Ý tưởng của nó như sau :

Cho X={xi} là tập hợp các vector trong không gian R^D(đây là R mũ D :v trong đây mình ko biết làm sao để viết công thức toán) và xi thuộc 1 trong 2 lớp yi= 1 hoặc yi= -1. Ta có tập điểm dữ liệu huấn luyện được biểu diễn như sau : {xi ,yi} với i=1,....n với yi ∈{-1 , 1}, n là số điểm dữ liệu huấn luyện.

Giả sử rằng dữ liệu là phân tách tuyến tính, nghĩa là có thể tìm được ít nhất một đường thẳng trên đồ thị của x1 và x2 phân tách 2 lớp khi D=2 và một siêu phẳng trên đồ thị của x1 , x2 , x3, ..., xD phân tách 2 lớp khi D>2.

=> Mục tiêu của SVM là xây dựng một siêu phẳng giữa 2 lớp sao cho khoảng cách từ nó tới các điểm gần siêu phẳng nhất của 2 lớp là cực đại. Siêu phẳng có thể được miêu tả bởi phương trình : ω.x + b = 0 trong đó :

• "." là phép nhân vô hướng véctơ.
• "ω" là véctơ pháp tuyến của siêu phẳng.
• b / || ω|| là khoảng cách vuông góc từ siêu phẳng đến gốc tọa độ.

Khi đó vector hỗtrợ (support vector) là những điểm dữ liệu gần siêu phẳng phân tách nhất. 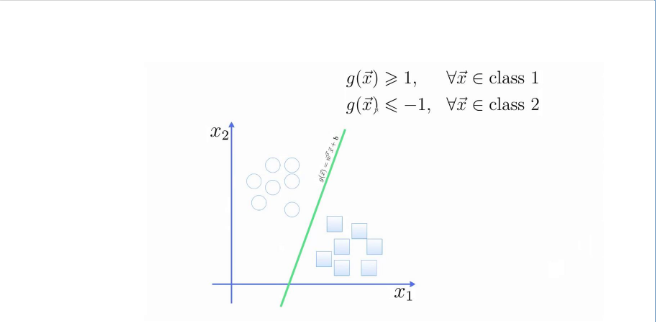Trên đây là đồ thị miêu tả về bài toán phân 2 lớp SVN.

Gọi z là khoảng cách từ các điểm gần mặt phân cách nhất của 2 lớp đến mặt phân cách ( hay còn gọi là lề). 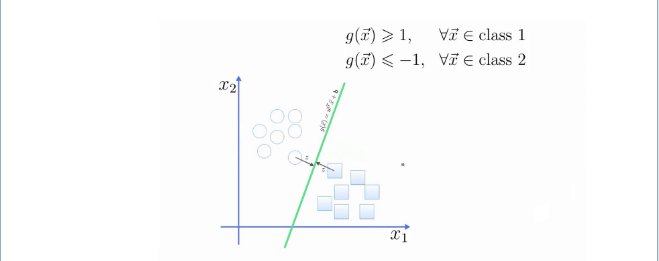Trên đây là mô tả của lề trong đồ thị của bài toán phân 2 lớp SVN.

Theo hình học không gian thì z=|g(x)| / ||ω||

• với lớp 1 thì g(x) ≥1 => z = 1||ω||. Tương tự như vậy với lớp 2.

và để z là cực đại thì ||ω || phải là cực tiểu => bài toán trở thành :

Tìm min || ω || thỏa mãn yi ( xi.ω+b) -1 ≥ 0 ∀xi.

Khi đã tìm được ω0 , b0 thỏa mãn điều kiện trên, một mẫu x’ sẽ được phân lớp.

Người ta chỉ ra rằng nếu các vector huấn luyện được phân tách mà không có lỗi bởi một siêu phẳng thì xác suất lỗi mắc phải trên một mẫu kiểm tra được giới hạn bởi tỉ lệ giữa giá trị kì vọng của số lượng vector hỗ trợ và sốlượng vector huấn luyện:

E[Pr(error)] = E[số vector hỗ trợ ] / số vector huấn luyện.

2.Lý thuyết nhân tử Lagrange

Vấn đề cực đại hàm f(x) thỏa điều kiện g(x) ≥ 0 sẽ được viết lại dưới dạng tối ưu của hàm Lagrange như sau:

                                      L(x,λ) ≡ f(x) + λg(x)

Trong đó x và λ phải thỏa điều kiện Karush-Kuhn-Tucker (KKT) như sau:

• g(x) ≥ 0

• λ ≥ 0

• λg(x) = 0

Nếu là cực tiểu hàm f(x) thì hàm Lagrange sẽ là

                                       L(x,λ) ≡ f(x) − λg(x)

====================================================================

Trên đây là phần giới thiệu về bài toán và các lý thuyết áp dụng cho phần sau Mô hình SVM cho bài toán 2 lớp.

Lần này mình tạm dừng ở đây để tiêu hóa phần này làm nền cho bài sau sẽ tiếp tục giới thiệu đến mọi nguời.

Cảm ơn vì đã quan tâm theo dõi!!!