Đã đăng vào thg 1 16, 8:00 SA 10 phút đọc

Paper reading | X3D: Expanding Architectures for Efficient Video Recognition

Đóng góp của bài báo

Ý tưởng cơ bản để xây dựng model cho các bài toán liên quan tới video đó là mở rộng kiến trúc mạng cho ảnh từ 2D theo chiều thời gian lên 3D. Bằng cách này, ta sẽ phải mở rộng input, filter, feature,... theo chiều thời gian. Tuy nhiên, điều này sẽ làm cho model trở nên rất lớn và yêu cầu nhiều tài nguyên tính toán.

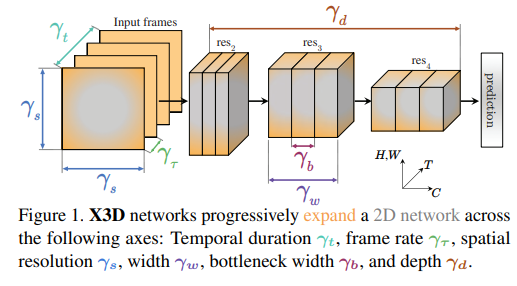
Bài báo đề xuất một kiến trúc mô hình có tên là X3D (Expand 3D), tên của mô hình mang ý nghĩa mở rộng từ không gian 2D sang không gian 3D Ý tưởng cốt lõi của mô hình là, trong khi việc mở rộng một mô hình nhỏ theo chiều thời gian (temporal axis) có thể làm tăng độ chính xác, tuy nhiên nếu xét trên khía cạnh cân bằng giữa độ chính xác và tài nguyên tính toán thì không phải lúc nào cũng là tốt nhất nếu ta so sánh với việc mở rộng mô hình theo các chiều khác. Xuất phát từ kiến trúc mô hình 2D nhỏ nhẹ sử dụng cho hình ảnh, nhóm tác giả mở rộng dần dần mô hình theo các chiều khác nhau (xem hình trên). Các chiều được nhóm tác giả đề xuất là: temporal duration $\gamma_t$ , frame rate $\gamma_\tau$ , spatial resolution $\gamma_s$ , network width $\gamma_w$ , bottleneck width $\gamma_b$ và depth $\gamma_d$ . Kết quả của việc mở rộng này là ta thu được một chuỗi các kiến trúc mô hình không thời gian (spatiotemporal) đảm bảo sự cân bằng và hiệu quả giữa độ chính xác và tài nguyên tính toán, có thể sử dụng cho nhiều trường hợp khác nhau.

Phương pháp

Các kiến trúc phân loại hình ảnh thường được phát triển bằng cách mở rộng các chiều như độ sâu của mạng (network depth), input resolution, độ rộng channel (channel width) từ mô hình trước đó. Tuy nhiên, cách này không được áp dụng cho các mô hình xử lý dữ liệu video trước đây, lý do là video khác ảnh là có thêm chiều thời gian và các mô hình thường mở rộng trực tiếp theo chiều thời gian này. Câu hỏi đặt ra là liệu việc mở rộng một kiến trúc 2D cố định thành 3D có phải là lý tưởng, hay là việc mở rộng hoặc thu hẹp theo các chiều khác có thể đạt được hiệu suất tốt nhất trong việc nhận diện video hay không?

Đối với việc phân loại video, chiều thời gian (temporal) đặt ra một vấn đề phụ khác, nó tạo ra nhiều khả năng mới nhưng cũng yêu cầu xử lý theo cách khác so với các chiều không gian (spatial). Cụ thể, nhóm tác giả đặt ra một số câu hỏi nghiên cứu như sau:

Chiến lược sampling theo chiều temporal tốt nhất trong một mô hình 3D là gì? Liệu sử dụng đầu vào dài và lấy mẫu thưa (ít hình ảnh trong một đoạn video) có tốt hơn là lấy mẫu tập trung từ các đoạn video ngắn?
Có cần thiết sử dụng độ phân giải không gian lớn cho việc phân loại video hay không? Một số nghiên cứu trước đó đã sử dụng độ phân giải thấp để tăng hiệu suất tính toán.
Nên sử dụng mạng với tốc độ khung hình cao (high frame-rate) nhưng độ phân giải kênh (channel resolution) thấp hơn, hay xử lý video một cách chậm rãi bằng một mô hình rộng hơn. Ví dụ như ta nên sử dụng các layer nặng hơn hay các layer có độ rộng nhỏ nhẹ hơn? Hay có cách nào cân bằng hơn không?
Khi tăng độ rộng mạng thì cách tốt nhất là tăng độ rộng mạng toàn cục hay là tăng độ rộng bottleneck bên trong?
Việc tăng độ sâu của mạng nên đi cùng với việc mở rộng input resolution để giữ cho kích thước receptive field đủ lớn và tỉ lệ mở rộng gần như không thay đổi hay là có cách mở rộng theo chiều khác tốt hơn?

Basis instantiation

Ta sẽ bắt đầu với mô hình X2D làm baseline. Mô hình X2D được thể hiện trong bảng trên nếu như $\gamma_\tau, \gamma_t, \gamma_s, \gamma_w, \gamma_b, \gamma_d$ đều có giá trị là 1.

Chi tiết kiến trúc X2D như sau:

Network resolution và channel capacity. Mô hình nhận đầu vào là một video clip thô được lấy mẫu với frame rate là $1/ \gamma_\tau$ . Mô hình sẽ nhận từng frame có kích thước là $T \times S^2 = 1 \times 112^2$ làm input, do $T = 1$ nên ta có thể coi đây là một mô hình phân loại hình ảnh. Độ rộng của từng layer được tăng lên gấp đôi sau mỗi phép lấy mẫu không gian (spatial sub-sampling) với bước (stride) = $1, 2^2$ tại từng stage sau (res2 đến res5). Mô hình cũng duy trì temporal input resolution cho tất cả các feature. Do đó, các tensor kích hoạt (activation tensors) chứa tất cả các frame theo chiều temporal, bảo toàn tần số thời gian đầy đủ trong tất cả các đặc trưng.
Network stages. Mô hình X2D bao gồm một chuỗi các stage và thiết kế bottleneck giống như mạng MobileNet sử dụng channel-wise separable convolution. Vì dữ liệu là video nên ta cần mở rộng spatial $3 \times 3$ convolution trong bottleneck block thành $3×3×3$ (hay $3×3^2$ ) spatiotemporal convolution.

Expansion operations

Sau khi định nghĩa xong kiến trúc X2D baseline, ta sẽ mở rộng lên thành kiến trúc X3D, là một spatiotemporal network bằng cách thay đổi các giá trị $\gamma_\tau, \gamma_t, \gamma_s, \gamma_w, \gamma_b, \gamma_d$ . Cụ thể:

X-Fast mở rộng temporal activation size $\gamma_t$ bằng cách tăng frame-rate $1/\gamma_\tau$ do đó tăng độ phân giải thời gian, nhưng duy trì thời lượng của đoạn video không đổi.
X-Temporal mở rộng temporal size $\gamma_t$ bằng cách lấy mẫu một đoạn video thời gian dài hơn và tăng frame rate $1/\gamma_\tau$ , nhằm mở rộng cả thời lượng và độ phân giải thời gian.
X-Spatial mở rộng độ phân giải không gian (spatial resolution) $\gamma_s$ bằng cách tăng độ phân giải không gian của mẫu video đầu vào.
X-Depth tăng độ sâu của mạng bằng cách tăng số lượng layer trên mỗi stage lên $\gamma_d$ lần.
X-Width mở rộng số lượng kênh (channel) đầu vào của tất cả các layer trong mạng bằng một hệ số mở rộng toàn cục $\gamma_w$ .
X-Bottleneck mở rộng kích thước kênh bên trong (inner channel width) $\gamma_b$ của convolutional filter trung tâm.

Progressive Network Expansion

Trong phần này, nhóm tác giả giới thiệu thuật toán để mở rộng mô hình một cách hiệu quả. Cụ thể ta có 2 hướng như sau:

Forward Expansion: Ban đầu, mô hình bắt đầu với X2D, là một phiên bản cơ bản với một tập hợp các hệ số mở rộng đơn vị $\mathcal{X}_0$ với số phần tử $a$ . Ta có $a = 6$ với $\mathcal{X} = {γ_τ, γ_t, γ_s, γ_w, γ_b, γ_d}$ , nhưng vẫn có thể bổ sung thêm các chiều khác. Mục tiêu của quá trình mở rộng là tìm các hệ số mở rộng $\mathcal{X}$ tạo ra sự cân bằng tốt nhất giữa hiệu suất (được đo bằng $J(\mathcal{X})$ ) và độ phức tạp (được đo bằng $C(\mathcal{X})$ ). Quá trình này tìm kiếm các hệ số mở rộng $\mathcal{X}$ với trade-off tốt nhất giữa hiệu suất và độ phức tạp. Ngoài ra, ta chỉ thay một trong số các hệ số mở rộng $a$ trong mỗi lần sửa đổi để đánh giá từng tập con khả thi $\mathcal{Z}$ .
Backward Contraction: Nếu việc mở rộng theo hướng Forward Expansion đến việc tăng độ phức tạp vượt quá mục tiêu ban đầu, một bước Backward Contraction được thực hiện để đảm bảo đạt được mức độ phức tạp mong muốn. Quá trình này đơn giản là giảm thiểu một phần cuối cùng của việc mở rộng gần nhất để phù hợp với mức độ phức tạp mong muốn. Ví dụ, nếu bước cuối cùng tăng frame-rate lên gấp đôi thì backward contraction sẽ giảm frame-rate đi <2 lần để đạt được độ phức tạp mong muốn.

Coding

import math
from functools import partial

import torch
import torch.nn as nn
import torch.nn.functional as F


class SubBatchNorm3d(nn.Module):
    """ FROM SLOWFAST """
    def __init__(self, num_splits, **args):
        super(SubBatchNorm3d, self).__init__()
        self.num_splits = num_splits
        self.num_features = args["num_features"]
        # Keep only one set of weight and bias.
        if args.get("affine", True):
            self.affine = True
            args["affine"] = False
            self.weight = torch.nn.Parameter(torch.ones(self.num_features))
            self.bias = torch.nn.Parameter(torch.zeros(self.num_features))
        else:
            self.affine = False
        self.bn = nn.BatchNorm3d(**args)
        args["num_features"] = self.num_features * self.num_splits
        self.split_bn = nn.BatchNorm3d(**args)

    def _get_aggregated_mean_std(self, means, stds, n):
        mean = means.view(n, -1).sum(0) / n
        std = (
            stds.view(n, -1).sum(0) / n
            + ((means.view(n, -1) - mean) ** 2).view(n, -1).sum(0) / n
        )
        return mean.detach(), std.detach()

    def aggregate_stats(self):
        """Synchronize running_mean, and running_var. Call this before eval."""
        if self.split_bn.track_running_stats:
            (
                self.bn.running_mean.data,
                self.bn.running_var.data,
            ) = self._get_aggregated_mean_std(
                self.split_bn.running_mean,
                self.split_bn.running_var,
                self.num_splits,
            )

    def forward(self, x):
        if self.training:
            n, c, t, h, w = x.shape
            x = x.view(n // self.num_splits, c * self.num_splits, t, h, w)
            x = self.split_bn(x)
            x = x.view(n, c, t, h, w)
        else:
            x = self.bn(x)
        if self.affine:
            x = x * self.weight.view((-1, 1, 1, 1))
            x = x + self.bias.view((-1, 1, 1, 1))
        return x


class Swish(nn.Module):
    """ FROM SLOWFAST """
    """Swish activation function: x * sigmoid(x)."""
    def __init__(self):
        super(Swish, self).__init__()

    def forward(self, x):
        return SwishEfficient.apply(x)


class SwishEfficient(torch.autograd.Function):
    """ FROM SLOWFAST """
    """Swish activation function: x * sigmoid(x)."""
    @staticmethod
    def forward(ctx, x):
        result = x * torch.sigmoid(x)
        ctx.save_for_backward(x)
        return result

    @staticmethod
    def backward(ctx, grad_output):
        x = ctx.saved_variables[0]
        sigmoid_x = torch.sigmoid(x)
        return grad_output * (sigmoid_x * (1 + x * (1 - sigmoid_x)))


def conv3x3x3(in_planes, out_planes, stride=1):
    return nn.Conv3d(in_planes,
                     out_planes,
                     kernel_size=3,
                     stride=(1,stride,stride),
                     padding=1,
                     bias=False,
                     groups=in_planes
                     )


def conv1x1x1(in_planes, out_planes, stride=1):
    return nn.Conv3d(in_planes,
                     out_planes,
                     kernel_size=1,
                     stride=(1,stride,stride),
                     bias=False)


class Bottleneck(nn.Module):
    def __init__(self, in_planes, planes, stride=1, downsample=None, index=0, base_bn_splits=8):
        super(Bottleneck, self).__init__()

        self.index = index
        self.base_bn_splits = base_bn_splits
        self.conv1 = conv1x1x1(in_planes, planes[0])
        self.bn1 = SubBatchNorm3d(num_splits=self.base_bn_splits, num_features=planes[0], affine=True) #nn.BatchNorm3d(planes[0])
        self.conv2 = conv3x3x3(planes[0], planes[0], stride)
        self.bn2 = SubBatchNorm3d(num_splits=self.base_bn_splits, num_features=planes[0], affine=True) #nn.BatchNorm3d(planes[0])
        self.conv3 = conv1x1x1(planes[0], planes[1])
        self.bn3 = SubBatchNorm3d(num_splits=self.base_bn_splits, num_features=planes[1], affine=True) #nn.BatchNorm3d(planes[1])
        self.swish = Swish() #nn.Hardswish()
        self.relu = nn.ReLU(inplace=True)
        if self.index % 2 == 0:
            width = self.round_width(planes[0])
            self.global_pool = nn.AdaptiveAvgPool3d((1,1,1))
            self.fc1 = nn.Conv3d(planes[0], width, kernel_size=1, stride=1)
            self.fc2 = nn.Conv3d(width, planes[0], kernel_size=1, stride=1)
            self.sigmoid = nn.Sigmoid()
        self.downsample = downsample
        self.stride = stride

    def round_width(self, width, multiplier=0.0625, min_width=8, divisor=8):
        if not multiplier:
            return width

        width *= multiplier
        min_width = min_width or divisor
        width_out = max(
            min_width, int(width + divisor / 2) // divisor * divisor
        )
        if width_out < 0.9 * width:
            width_out += divisor
        return int(width_out)


    def forward(self, x):
        residual = x

        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)

        out = self.conv2(out)
        out = self.bn2(out)
        # Squeeze-and-Excitation
        if self.index % 2 == 0:
            se_w = self.global_pool(out)
            se_w = self.fc1(se_w)
            se_w = self.relu(se_w)
            se_w = self.fc2(se_w)
            se_w = self.sigmoid(se_w)
            out = out * se_w
        out = self.swish(out)

        out = self.conv3(out)
        out = self.bn3(out)

        if self.downsample is not None:
            residual = self.downsample(x)

        out += residual
        out = self.relu(out)

        return out


class ResNet(nn.Module):

    def __init__(self,
                 block,
                 layers,
                 block_inplanes,
                 n_input_channels=3,
                 shortcut_type='B',
                 widen_factor=1.0,
                 dropout=0.5,
                 n_classes=400,
                 base_bn_splits=8,
                 task='class'):
        super(ResNet, self).__init__()

        block_inplanes = [(int(x * widen_factor),int(y * widen_factor)) for x,y in block_inplanes]
        self.index = 0
        self.base_bn_splits = base_bn_splits
        self.task = task

        self.in_planes = block_inplanes[0][1]

        self.conv1_s = nn.Conv3d(n_input_channels,
                               self.in_planes,
                               kernel_size=(1, 3, 3),
                               stride=(1, 2, 2),
                               padding=(0, 1, 1),
                               bias=False)
        self.conv1_t = nn.Conv3d(self.in_planes,
                               self.in_planes,
                               kernel_size=(5, 1, 1),
                               stride=(1, 1, 1),
                               padding=(2, 0, 0),
                               bias=False,
                               groups=self.in_planes)
        self.bn1 = SubBatchNorm3d(num_splits=self.base_bn_splits, num_features=self.in_planes, affine=True) #nn.BatchNorm3d(self.in_planes)
        self.relu = nn.ReLU(inplace=True)
        self.layer1 = self._make_layer(block,
                                       block_inplanes[0],
                                       layers[0],
                                       shortcut_type,
                                       stride=2)
        self.layer2 = self._make_layer(block,
                                       block_inplanes[1],
                                       layers[1],
                                       shortcut_type,
                                       stride=2)
        self.layer3 = self._make_layer(block,
                                       block_inplanes[2],
                                       layers[2],
                                       shortcut_type,
                                       stride=2)
        self.layer4 = self._make_layer(block,
                                       block_inplanes[3],
                                       layers[3],
                                       shortcut_type,
                                       stride=2)
        self.conv5 = nn.Conv3d(block_inplanes[3][1],
                               block_inplanes[3][0],
                               kernel_size=(1, 1, 1),
                               stride=(1, 1, 1),
                               padding=(0, 0, 0),
                               bias=False)
        self.bn5 = SubBatchNorm3d(num_splits=self.base_bn_splits, num_features=block_inplanes[3][0], affine=True) #nn.BatchNorm3d(block_inplanes[3][0])
        if task == 'class':
            self.avgpool = nn.AdaptiveAvgPool3d((1, 1, 1))
        elif task == 'loc':
            self.avgpool = nn.AdaptiveAvgPool3d((None, 1, 1))
        self.fc1 = nn.Conv3d(block_inplanes[3][0], 2048, bias=False, kernel_size=1, stride=1)
        self.fc2 = nn.Linear(2048, n_classes)
        self.dropout = nn.Dropout(dropout)

        for m in self.modules():
            if isinstance(m, nn.Conv3d):
                nn.init.kaiming_normal_(m.weight,
                                        mode='fan_out',
                                        nonlinearity='relu')

    def _downsample_basic_block(self, x, planes, stride):
        out = F.avg_pool3d(x, kernel_size=1, stride=stride)
        zero_pads = torch.zeros(out.size(0), planes - out.size(1), out.size(2),
                                out.size(3), out.size(4))
        if isinstance(out.data, torch.cuda.FloatTensor):
            zero_pads = zero_pads.cuda()

        out = torch.cat([out.data, zero_pads], dim=1)

        return out

    def _make_layer(self, block, planes, blocks, shortcut_type, stride=1):
        downsample = None
        if stride != 1 or self.in_planes != planes[1]:
            if shortcut_type == 'A':
                downsample = partial(self._downsample_basic_block,
                                     planes=planes[1],
                                     stride=stride)
            else:
                downsample = nn.Sequential(
                    conv1x1x1(self.in_planes, planes[1], stride),
                    SubBatchNorm3d(num_splits=self.base_bn_splits, num_features=planes[1], affine=True) #nn.BatchNorm3d(planes[1])
                    )

        layers = []
        layers.append(
            block(in_planes=self.in_planes,
                  planes=planes,
                  stride=stride,
                  downsample=downsample,
                  index=self.index,
                  base_bn_splits=self.base_bn_splits))
        self.in_planes = planes[1]
        self.index += 1
        for i in range(1, blocks):
            layers.append(block(self.in_planes, planes, index=self.index, base_bn_splits=self.base_bn_splits))
            self.index += 1

        self.index = 0
        return nn.Sequential(*layers)


    def replace_logits(self, n_classes):
        self.fc2 = nn.Linear(2048, n_classes)


    def update_bn_splits_long_cycle(self, long_cycle_bn_scale):
        for m in self.modules():
            if isinstance(m, SubBatchNorm3d):
                m.num_splits = self.base_bn_splits * long_cycle_bn_scale
                m.split_bn = nn.BatchNorm3d(num_features=m.num_features*m.num_splits, affine=False).to(m.weight.device)
        return self.base_bn_splits * long_cycle_bn_scale


    def aggregate_sub_bn_stats(self):
        """find all SubBN modules and aggregate sub-BN stats."""
        count = 0
        for m in self.modules():
            if isinstance(m, SubBatchNorm3d):
                m.aggregate_stats()
                count += 1
        return count


    def forward(self, x):
        x = self.conv1_s(x)
        x = self.conv1_t(x)
        x = self.bn1(x)
        x = self.relu(x)

        x = self.layer1(x)
        x = self.layer2(x)
        x = self.layer3(x)
        x = self.layer4(x)

        x = self.conv5(x)
        x = self.bn5(x)
        x = self.relu(x)

        x = self.avgpool(x)

        x = self.fc1(x)
        x = self.relu(x)

        if self.task == 'class':
            x = x.squeeze(4).squeeze(3).squeeze(2) # B C
            x = self.dropout(x)
            x = self.fc2(x).unsqueeze(2) # B C 1
        if self.task == 'loc':
            x = x.squeeze(4).squeeze(3).permute(0,2,1) # B T C
            x = self.dropout(x)
            x = self.fc2(x).permute(0,2,1) # B C T

        return x


def replace_logits(self, n_classes):
        self.fc2 = nn.Linear(2048, n_classes)


def get_inplanes(version):
    planes = {'S':[(54,24), (108,48), (216,96), (432,192)],
              'M':[(54,24), (108,48), (216,96), (432,192)],
              'XL':[(72,32), (162,72), (306,136), (630,280)]}
    return planes[version]


def get_blocks(version):
    blocks = {'S':[3,5,11,7],
              'M':[3,5,11,7],
              'XL':[5,10,25,15]}
    return blocks[version]


def generate_model(x3d_version, **kwargs):
    model = ResNet(Bottleneck, get_blocks(x3d_version), get_inplanes(x3d_version), **kwargs)
    return model

Thực nghiệm

Biểu đồ dưới thể hiện độ chính xác và độ phức tạp của mô hình khi mở rộng theo các chiều khác nhau từ model base X2D ban đầu.

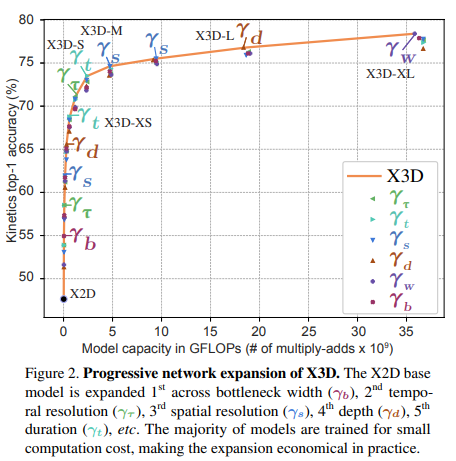
Cụ thể hơn, các phiên bản model được thể hiện trong bảng sau:

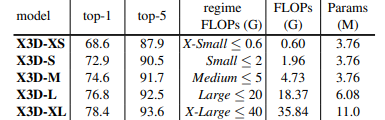
Kiến trúc cụ thể của từng phiên bản model X3D được thể hiện trong hình dưới.

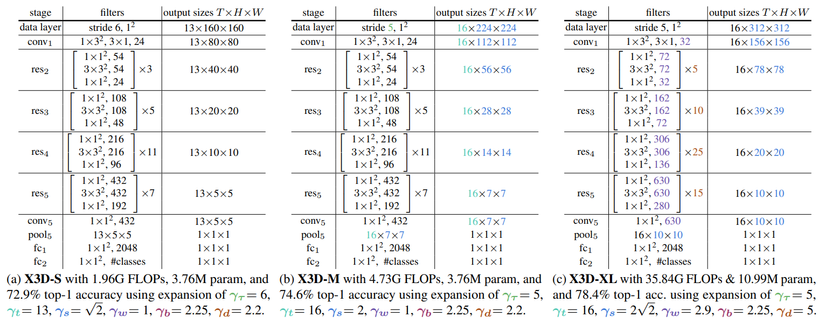
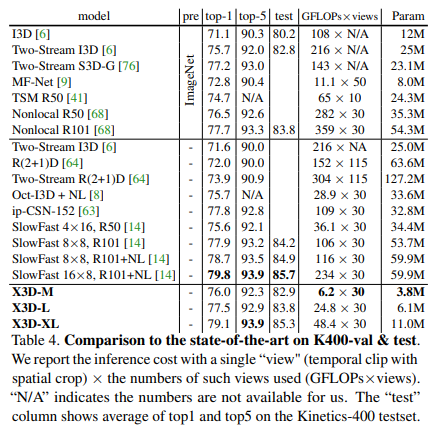
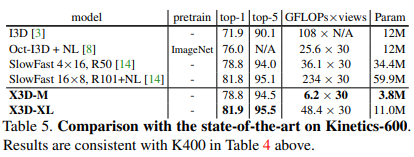
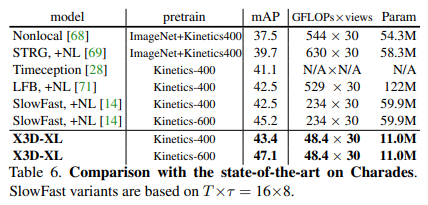
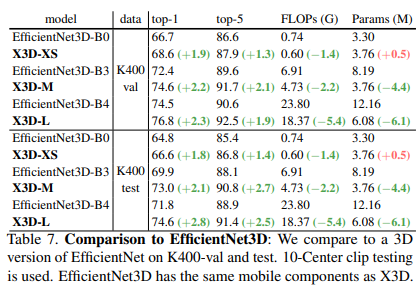
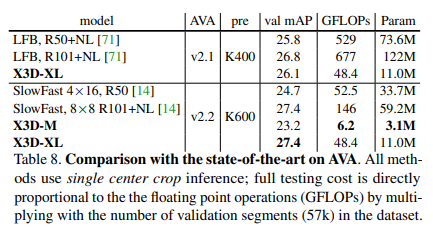
Một số so sánh kết quả giữa mô hình X3D và các model SOTA trước đó trên bộ dữ liệu Kinetic-400, Kinetic-600 và AVA dataset được thể hiện trong các bảng sau: