[Paper Explained] Triple-Sigmoid Activation Function for Deep Open-Set Recognition
Bài đăng này đã không được cập nhật trong 3 năm
1. Bài toán Open-Set Recognition
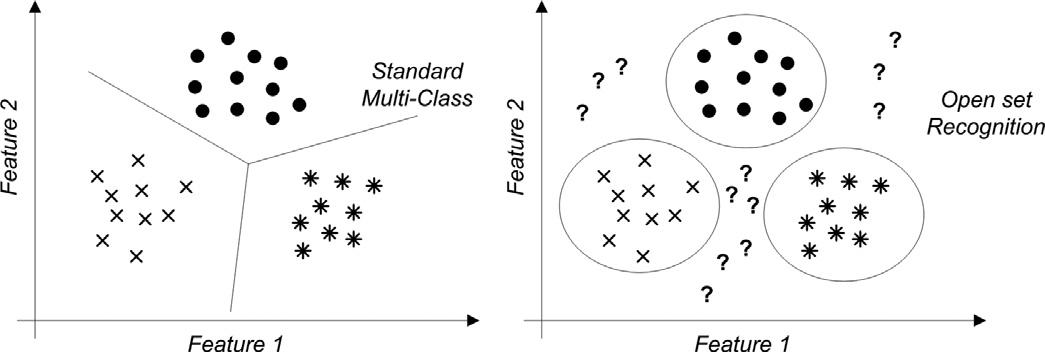
Thông thường, với các bài toán classification, ta thường hay train một mô hình học máy học có giám sát trên một bộ training set với số lượng class nhất định và test mô hình đó trên một bộ test set có cùng các class với bộ đã được dùng để train. Khi đó, model sẽ chỉ thực hiện được task Closed-Set Recognition, nghĩa là classify một input vào một trong những class mà model đã được huấn luyện. Nếu gặp một input có class không nằm trong bộ train, model sẽ dự đoán class của input là một trong những class đã được train, từ đó đưa ra kết quả sai. Điều này làm cho việc deploy model trong thực tế gặp khó khăn bởi ngoài việc model classify được các class đã được train, ta cần nó phải phân biệt được một input có thuộc vào các class mà nó đã được train hay không để từ đó đưa ra các quyết định hợp lý. Task này được gọi là Open-Set Recognition.
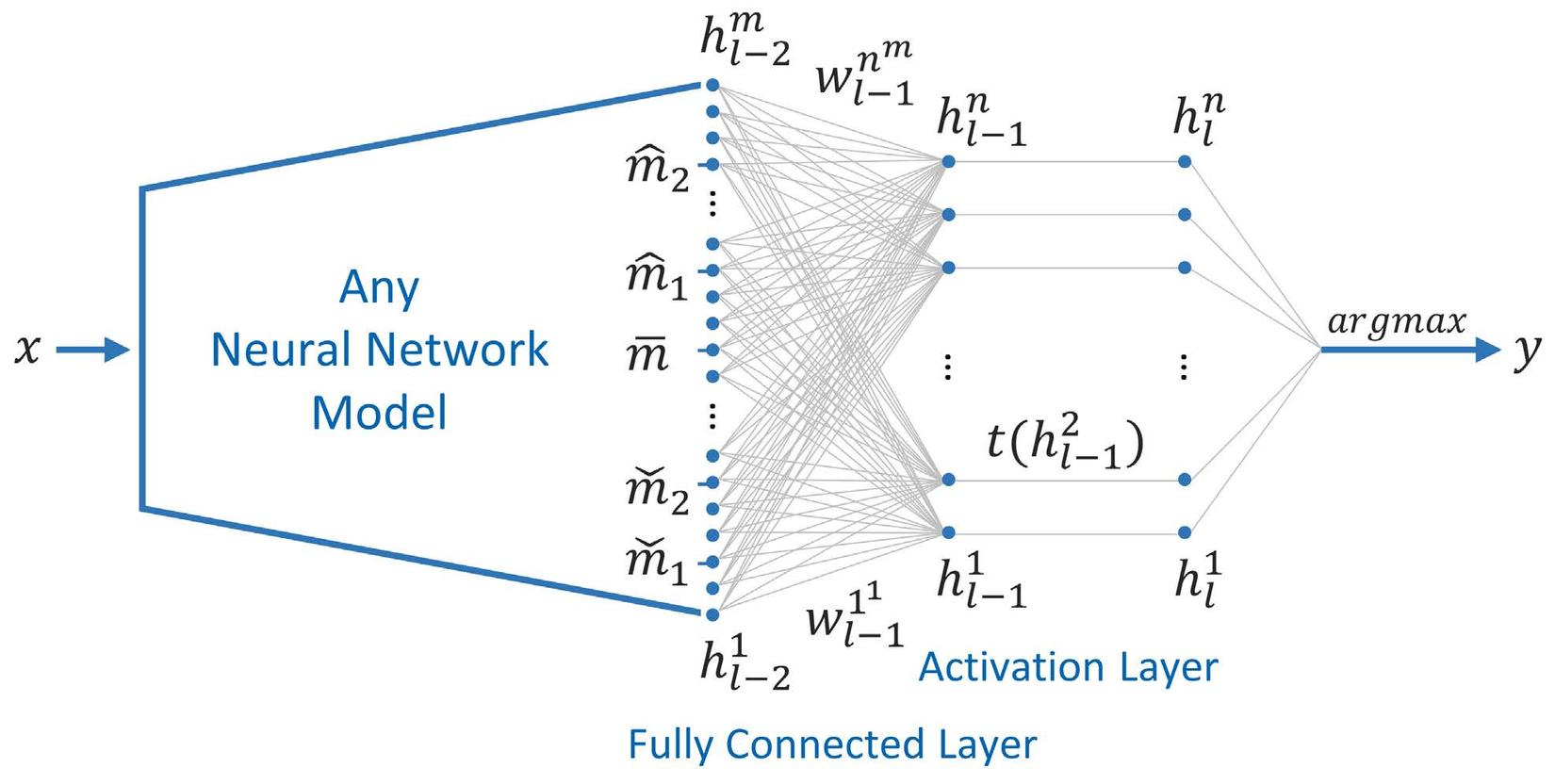
Trong bài toán classification, ta có một model với tham số . Với một input sample , model sẽ predict ra class với () là các class mà model được train. Theo như hình minh hoạ ở trên, sẽ nhận index của logit tại layer cuối (layer thứ ) mà có giá trị lớn nhất trong logit (tương ứng với class), hay . Tuy nhiên, điều này chỉ áp dụng cho Closed-Set Recognition. Còn với Open-Set Recognition, ta sẽ có hàm như sau:
- Với có class nằm trong bộ train (hay x là inlier): với .
- Với có class nằm ngoài bộ train (hay x là outliet):
2. Phân tích toán học
Thông thường, ở layer cuối , ta thường dùng hàm Softmax hoặc Sigmoid để các logit nhận một số thực trong khoảng . Để giải quyết bài toán Open-Set Recognition, ta có thể chọn cách đơn giản nhất là dùng một threshold để xác định xem là inlier hay outlier. sẽ được coi như là một outlier nếu như . Do đó, với các input sample là outlier, ta kỳ vọng là sẽ gần nhất có thể. Tuy nhiên:
- Hàm Softmax lại không phù hợp với phương pháp này do không thể đồng thời gần 0 vì .
- Với hàm Sigmoid, ta cũng có thể dùng một threshold như trên. Tuy nhiên, theo [2], các outlier cũng có thể sinh ra logit lớn hơn threshold này. Do đó, hàm Sigmoid cũng không thể đảm bảo được là các logit sẽ nhỏ hơn threshold.
Giả sử trong trường hợp có 2 class (), threshold và hàm activation ở layer cuối là Sigmoid, với input sample là inlier, một trong hai logit ở layer cuối hoặc phải lớn hơn hoặc bằng . Để điều đó xảy ra, một trong hai logit hoặc sẽ phải lớn hơn . Với là outlier, cả và phải nhỏ hơn , hay và nhỏ hơn 0.
Do việc training chỉ được thực hiện với các inlier, tham số sẽ được tối ưu để có thể được dùng để phân biệt hai class. Ví dụ, coi các logit là các logit được dùng để nhận diện class 1, còn là để nhận diện class 2. Ngoài ra, để đơn giản hoá việc giải thích, ta sẽ coi như chỉ nhận giá trị hoặc (thay vì từ đến ). Với giả sử trên, đối với các sample thuộc class 1, sẽ nhận giá trị là , còn sẽ nhận giá trị là . Điều ngược lại cũng sẽ xảy ra khi input sample thuộc class 2. Như vậy, với input sample thuộc class 1, ta cần và (để và ). Còn với các sample thuộc class 2, ta cần và (để và ).
Lúc inference với input sample là outlier, ta có thể gặp các trường hợp sau với layer :
- Trường hợp hiếm gặp nhất sẽ là bị nhận nhầm thành inlier khi toàn bộ logit của layer này bằng 0. Khi đó, , tương đương với việc .
- Trường hợp khác, layer này sẽ có một vài logit liên quan đến class 1 (giả sử với ) và class 2 (giả sử với ) nhận giá trị và các logit còn lại nhận giá trị . Để cho và nhỏ hơn , ta cần cả và nhỏ hơn .
Trong quá trình training với hai class đã biết trước, và sẽ là số dương, còn và sẽ là số âm (do được dùng để nhận diện class 1, được dùng để nhận diện class 2). Điều này kéo theo và thường nhận số dương, trong khi và thường nhận số âm. Để tổng của một số âm và số dương là một số âm, ta cần số dương phải nhỏ hơn trị tuyệt đối của số âm. Khi train model, một trong hai và phải là số dương và cái còn lại là số âm. Khi inference, nếu như phần số âm càng trở nên âm, còn phần số dương trở nên càng nhỏ, xác suất và nhận giá trị âm khi input là outlier sẽ càng tăng.
3. Hàm activation Triple-Sigmoid
Dựa trên quan sát trên, tác giả bài báo đã đề xuất việc sử dụng hàm activation Triple-Sigmoid bao gồm 3 hàm Sigmoid con. Mục đích của hàm Triple-Sigmoid là để phạt các giá trị của và , cũng như giúp ta dùng được threshold để dễ dàng xác định xem input là inlier hay outlier. Đồ thị của hàm Triple-Sigmoid sẽ có dạng như hình dưới đây. Trong hàm Triple-Sigmoid, hàm Sigmoid 1 sẽ dùng để làm cho logit âm trở nên âm nhất có thể, còn Sigmoid 2 và 3 để làm cho logit dương nhỏ nhất có thể.
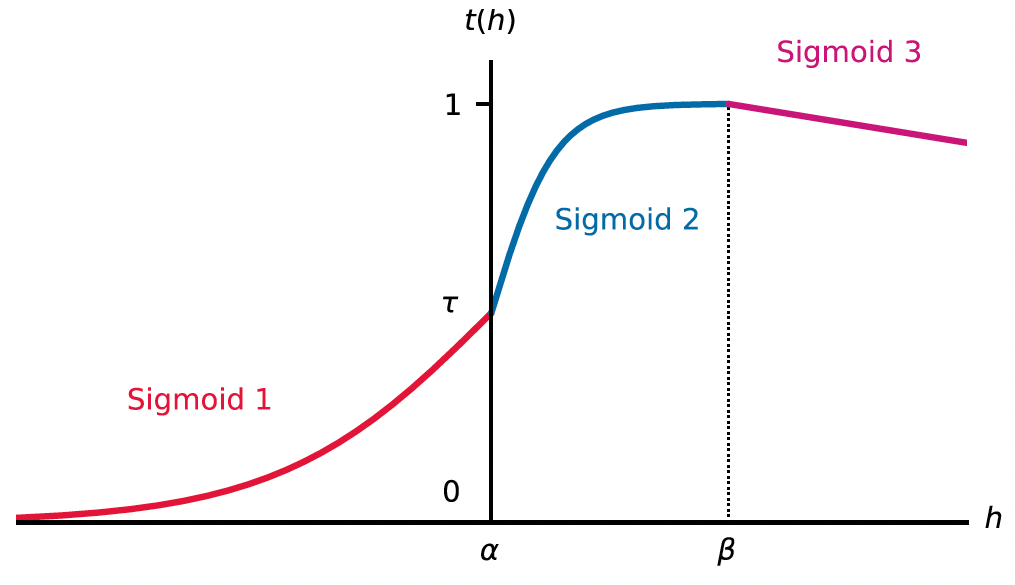
Công thức toán học của hàm Triple-Sigmoid như sau:
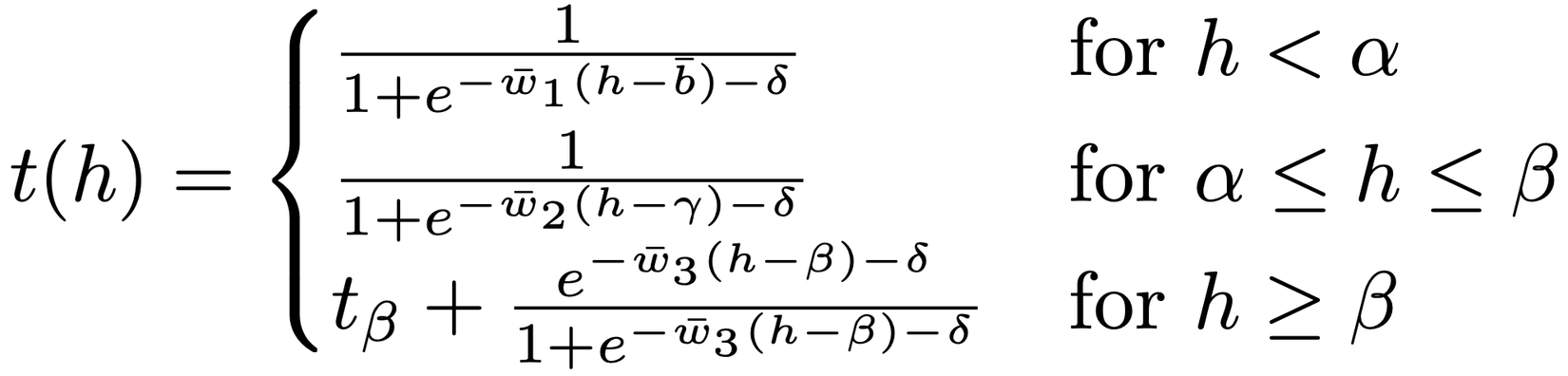
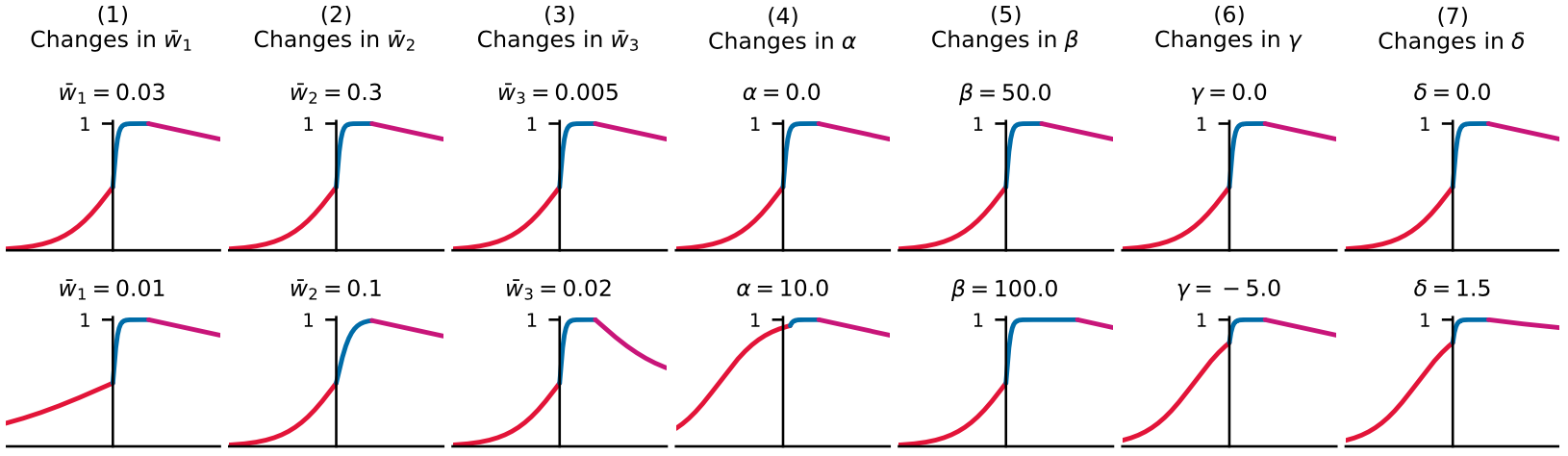
trong đó, là output của hidden layer. Hàm Triple-Sigmoid có 3 nhánh với tất cả 7 parameter:
- , , : lần lượt dùng để điều chỉnh độ dốc của hàm Sigmoid 1, 2, 3.
- : dùng để điều chỉnh điểm giao (trên trục x) giữa Sigmoid 1 và 2.
- : dùng để điều chỉnh điểm giao (trên trục x) giữa Sigmoid 2 và 3.
- : dùng để điều chỉnh điểm giao (trên trục y) giữa Sigmoid 1 và 2.
- : dùng để điều chỉnh độ nghiêng của Sigmoid 3 và điểm giao (trên trục y) giữa Sigmoid 1 và 2.
Có hai biến và sẽ không được chỉnh bằng tay. Điều này là do ta cần Sigmoid 1 và 2 phải có cùng giá trị tại cũng như Sigmoid 2 và 3 phải có cùng giá trị tại . Công thức tính và như sau:
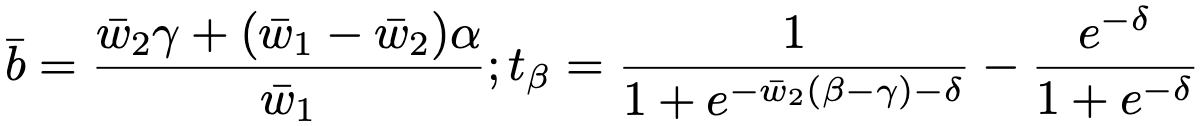
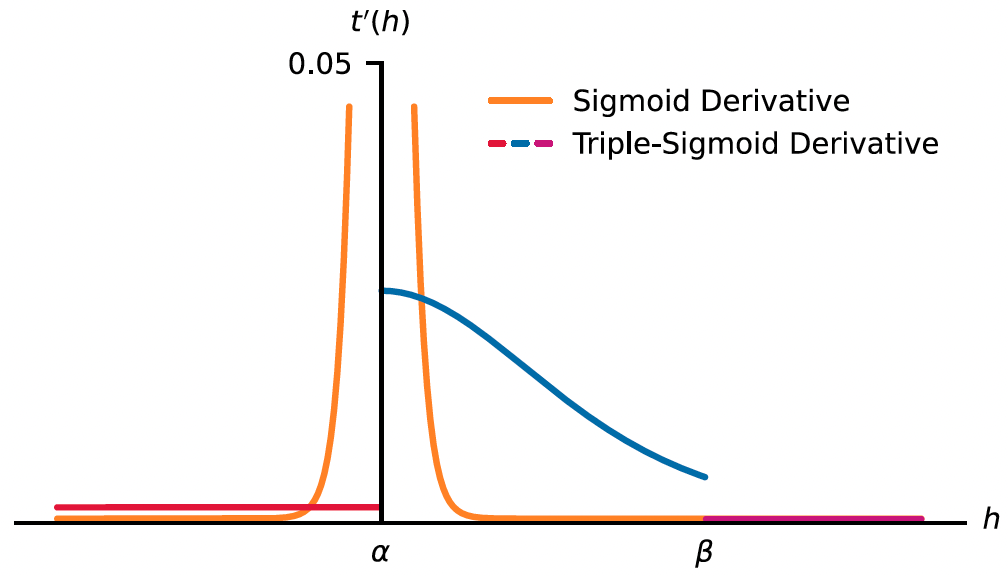
Dưới đây là đồ thị đạo hàm của Triple-Sigmoid. Có thể thấy giá trị đạo hàm tại hai khúc và rất nhỏ, trong khi tại khúc thì lại lớn hơn. Điều này là để phạt mạnh hơn các negative sample bị dự đoán sai, đẩy logit của layer mạnh hơn về bên trái, giúp giảm thiểu việc các logit này nhận giá trị lớn hơn threshold khi input là outlier như trong [2] chỉ ra.
4. Kết quả thí nghiệm
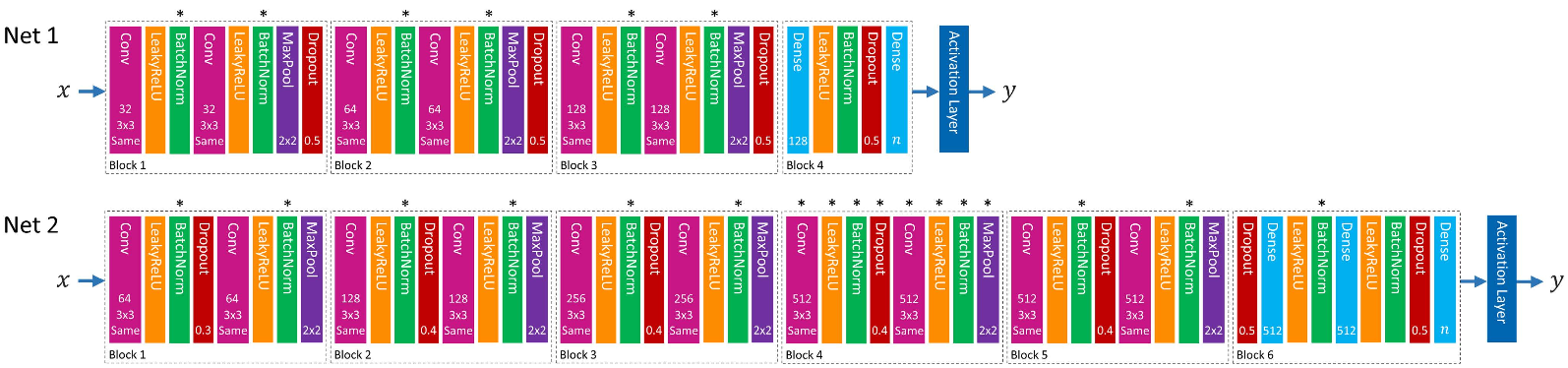
Trong bài báo, các thí nghiệm được thực hiện bằng 2 model Net 1 và Net 2 (tương tự VGG-13).
Với hàm Triple-Sigmoid, các tham số , , , , , được set lần lượt là , , , , và . Riêng thì được chọn là khi dùng với bộ MNIST và với các trường hợp còn lại.
4.1. Closed-Set Recognition
Với các bộ dataset như MNIST, SVHN và CIFAR10, mỗi bộ sẽ có 6/10 class được chọn ngẫu nhiên làm một closed set. Riêng đối với bộ CIFAR+10 thì có 4 class liên quan đến phương tiện giao thông. Theo kết quả so sánh với các hàm activation khác, model Net 1 dùng Triple-Sigmoid có kết quả ngang ngửa với các hàm activation khác.
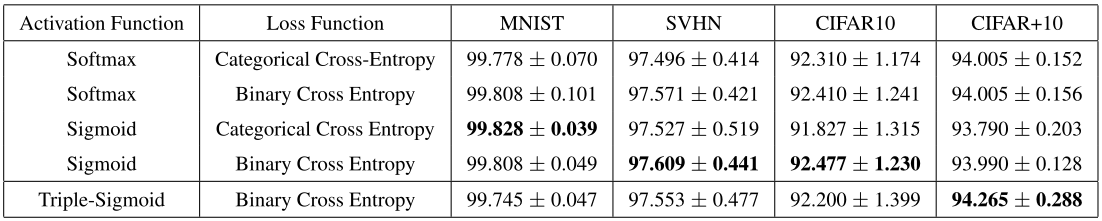
4.2. Open-Set Recognition
4.2.1. So sánh với các hàm activation thông thường
Với các bộ dataset như MNIST, SVHN và CIFAR10, các class còn lại của thí nghiệm trên được chọn làm outlier (class thứ ). Với bộ CIFAR+10, outlier sẽ là 10/50 class liên quan đến động vật được chọn ngẫu nhiên. Ngoài ra, bộ CIFAR+50 gồm 4 class phương tiện giao thông từ CIFAR10 làm inlier và 50 class động vật từ CIFAR100 được lấy từ CIFAR100 làm outlier cũng được dùng. Đồng thời, trong các thí nghiệm này, threshold được set bằng để phân biệt inlier và outlier.

Kết quả F1-score riêng cho class thứ ở trên cho thấy model dùng Triple-Sigmoid có khả năng phát hiện outlier mạnh hơn so với dùng hàm Softmax và Sigmoid thông thường. Điều này được giải thích bằng bảng phân bố logit của layer với input là outlier ở dưới đây (riêng hàm Softmax thì khó visualize nên thay vào đó, tác giả đã visualize bằng phân bố của logit lớn nhất tại layer cuối ). Trong bảng phân bố này, ta có thể thấy hàm Softmax cùng với 2 kiểu loss Categorial and Binary Cross Entropy đều cho ra giá trị của layer cuối gần với 1, lớn hơn rất nhiều so với threshold . Với model dùng Sigmoid được train với Categorial Cross Entropy, model không hề có khả năng phát hiện ra outlier vì các logit đều lớn hơn làm cho layer cuối lớn hơn threshold. Khi train với Binary Cross Entropy, việc classify outlier của model này được cải thiện hơn khi distribution của dịch qua trục về phía bên trái. Còn với Triple-Sigmoid, phân bố logit của outlier đa phần nằm ở bên trái trục , nhất là với MNIST, SVHN, CIFAR+50. Do đó, số lượng outlier được phát hiện cũng nhiều hơn so với các phương pháp trên.
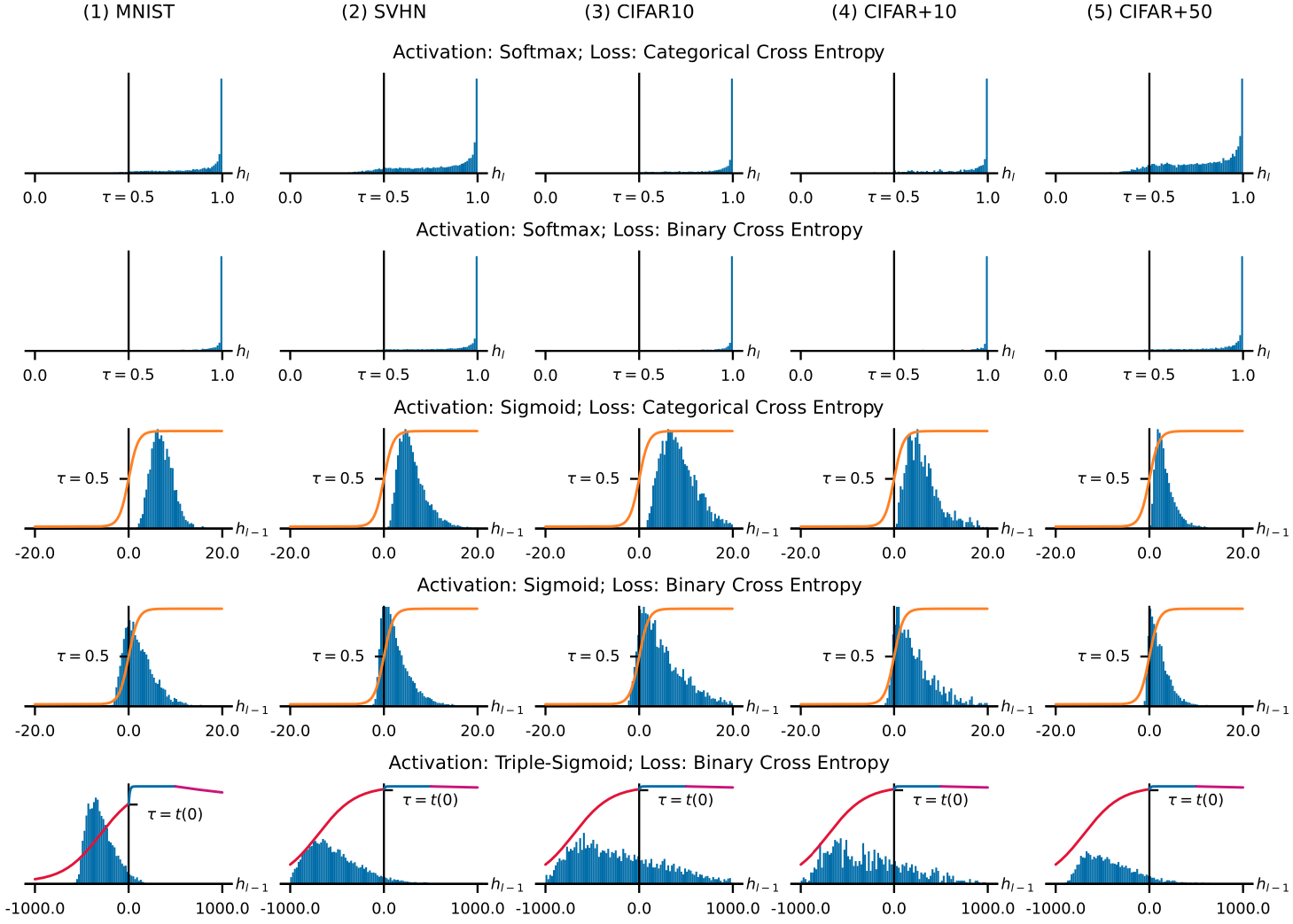
4.2.2. So sánh với các phương pháp khác

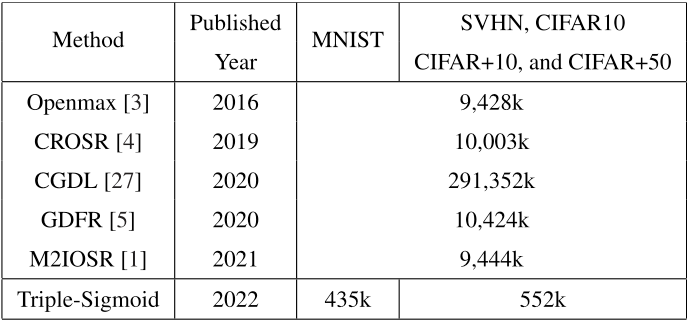
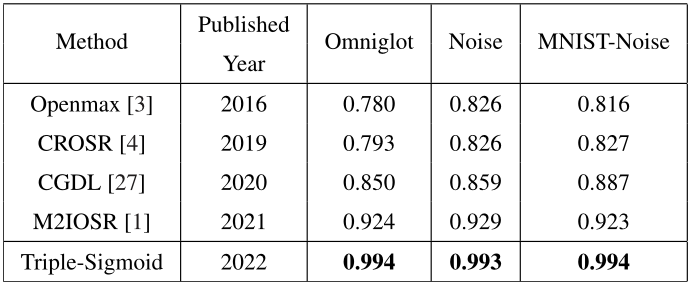
Kết quả so sánh model Net 1 dùng Triple-Sigmoid với các phương pháp SOTA khác trên các bộ dataset như MNIST, SVHN, CIFAR10/+10/+50 cho thấy ngoài việc outperform đáng kể các phương pháp khác trên các task, việc dùng Triple-Sigmoid còn giúp cho model có lượng parameters ít hơn nhiều lần so với các phương pháp khác.
So với các phương pháp SOTA khác bằng model Net 2, phương pháp dùng Triple-Sigmoid cũng outperform toàn bộ với F1-score cao hơn đáng kể so với các phương pháp khác trên các bộ dataset phức tạp hơn.
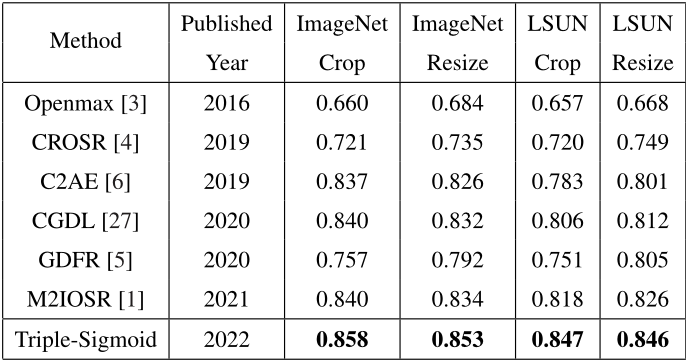
Tài liệu tham khảo:
All rights reserved
