9.8K 583 32

Đã đăng vào thg 10 26, 2015 6:13 SA 26 phút đọc

3.3K

Open-Closed Principle

Bài đăng này đã không được cập nhật trong 3 năm

Tiếp nối loạt bài viết dịch cuốn sách "Agile Software Development, Principles Patterns and Practices", ngày hôm nay, chúng ta đến với nguyên tắc thức hai trong thiết kế linh hoạt, đó là OCP.

Nguyên tắc đóng mở - Open-Closed Principle

Dutch Door - (danh từ) Một cánh cửa được chia làm hai phần theo chiều ngang, do vậy mỗi thành phần đều có thể mở sang trái hoặc đóng.

The American Heritage - Dictionary of the English Language: Fourth Edition. 2000

Ivar từng nói, "Tất cả hệ thống đều thay đổi trong vòng đời của nó. Cần luôn có trong đầu suy nghĩ xây dựng một hệ thống tồn tại lâu dài hơn những phiên bản đầu tiên". Làm cách nào để chúng ta thiết kế những phiên bản ổn định với những thay đổi và tổn tại lâu dài? Betrand Meyer cho chúng ta định hướng từ năm 1988 với cái tên Nguyên tắc đóng mở (Open-Closed Principle).

OCP: Nguyên tắc đóng mở (Open-Closed Principle)

Các thành phần của phần mềm (class, mô-đun, hàm,...) cần mở cho sự mở rộng nhưng đóng với sự thay đổi

Khi một thay đổi ở chương trình dẫn đến thay đổi ở nhiều thành phần, thiết kế sẽ có mùi cứng nhắc (Rigidity). OCP cho chúng ta lời khuyên về việc tái cấu trúc chương trình, để các thay đổi sẽ không gây nên quá nhiều thay đổi trong các thành phần của chương trình. Nếu OCP được thực hiện đúng, những thay đổi kiểu này sẽ đạt được bằng việc viết thêm những dòng code, không phải thay đổi những dòng code cũ đã hoạt động tốt.

Đây có vẻ là mục tiêu quá xa vời - một mục tiêu vàng gần như không thể đạt được - tuy nhiên, thực tế có khá nhiều chiến lược đơn giản và hiệu quả giúp đạt được lý tưởng này.

Mô tả

Mô-đun thoả mãn nguyên tắc đóng mở sẽ có hai tính chất.

"Mở cho sự mở rộng" - "Open for extension"

Điều đó có nghĩa là hành vi của mô-đun có thể mở rộng. Khi yêu cầu hệ thống thay đổi, chúng ta có thể mở rộng mô-đun để có thể đáp ứng các hành vi mới thoả mãn yêu cầu. Nói một cách khác, chúng ta có thể thay đổi cách mà mô-đun làm việc.

"Đóng với sự thay đổi" - "Closed for modification"

Mở rộng mô-đun không kéo theo việc thay đổi mã nguồn của mô-đun. Tập tin chứa mã nhị phân đóng vai trò thực thi của mô-đun, hoặc là các thư viện liên kết, DLL hay Java .jar đều không bị đụng chạm đến.

Có vẻ hai tính chất này đang mâu thuẫn và trái ngược nhau. Các thông thường để mở rộng hành vi của mô-đun là thay đổi nó. Một mô-đun không bị thay đổi thông thường đã có hành vi cố định.

Làm cách nào để một mô-đun có thể được thay đổi mà không thay đổi mã nguồn của nó? Làm cách nào để thay đổi cách mà mô-đun làm việc, nhưng không thay đổi mô-đun?

Trừu tượng là chìa khoá

Trong C++, Java hay bất cứ ngôn ngữ lập trình hướng đối tượng nào (OOPL), chúng ta có thể trừu tượng hóa các hành vi quy định ngay từ trước trong một nhóm không giới hạn các hành vi có thể. Sự trừu tượng thể hiện ở class trừu tượng cơ sở, trong khi một lương không giới hạn các hành vi có thể được thể hiện ở các class thừa kế từ class cơ sở.

Chúng ta hoàn toàn có thể điều khiển một mô-đun dưới hình thức trừu tượng. Những mô-đun như vậy có thể đóng với sự thay đổi bởi chúng phụ thuộc vào một lớp trừu tượng đã được cố định. Tuy nhiên, hành vi của mô-đun đó có thể mở rộng bằng cách tạo ra class phát sinh từ lớp trừu tượng.

Hình 9-1 mô tả một thiết kế đơn giản không thỏa mãn OCP. Cả class Client và Server đều rời rạc. Client sử dụng class Server. Nếu chúng ta mong chờ đối tượng Client sử dụng các đối tượng Server khác nhau, class Client cần thay đổi để gọi tên class Server mới.

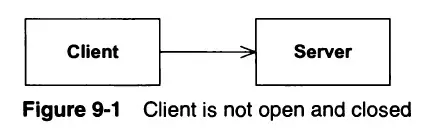
Hình 9-2 cho thấy một thiết kế phù hợp, thỏa mãn OCP. Trong trường hợp này, class ClientInterface là một lớp trừu tượng với phương thức trừu tượng. Class Client sử dụng tính trừu tượng này, tuy nhiên đối tượng của class Client cần sử dụng đối tượng được sinh ra từ class Server. Nếu chúng ta muốn đối tượng của class Client sử dụng đối tượng khác của class Server, khi đó một phiên bản khác sinh ra từ ClientInterface có thể được tạo ra. Do vậy, class Client có thể giữ không đổi.

Class Client có một vài công việc cần làm, do vậy nó định nghĩa những công việc đó trong lớp trừu tượng ClientInterface. Các lớp con của ClientInterface có thể định nghĩa theo bất kỳ cách nào mà chúng muốn. Do vậy, hành vi của Client có thể mở rộng và thay đổi bằng cách tạo ra lớp con của ClientInterface.

Bạn có thể đặt câu hỏi, tại sao tôi đặt tên là ClientInterface như trên. Tại sao tôi không gọi là AbstractInterface? Lý do, sẽ như những gì chúng ta thấy ở sau, class trừu tượng sẽ gần gũi với class sử dụng nó hơn là class thực hiện nó.

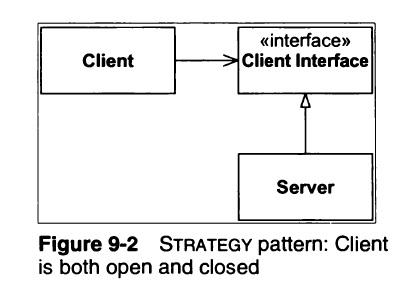
Hình 9-3 mô tả một kiến trúc khác. Class Policy có một tập các phương thức công khai nhằm thực hiện chính sách của một vài đối tượng. Giống như với các phương thức của Client ở hình 9-2. Cũng như trên, những hàm thực hiện chính sách đó định nghĩa một số công việc cần được thực hiện trong phạm trù của một lớp trừu tượng. Tuy nhiên, trong trường hợp này, lớp trừu tượng là một phần của chính lớp Policy. Trong C++, nó cần là một hàm ảo thuần túy (pure virtual function) và trong Java chúng cần là phương thức trừu tượng (abstract method). Những hàm này được định nghĩa trong các lớp kế cận của Policy. Do vậy, các hành vi được đưa ra trong class Policy có thể mở rộng và thay đổi trong các lớp kế cận được sinh ra từ Policy.

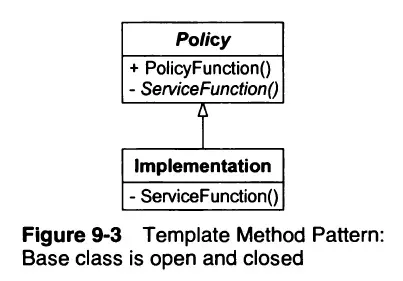
Hai mô hình trên là hai cách phổ biến nhất để thỏa mãn OCP. Nó cho thấy sự tách biệt rõ ràng giữa các hàm tổng quát với các hàm chi tiết được tạo ra.

Ứng dụng Shape

Ví dụ sau được nêu ra trong rất nhiều sách về thiết kế hướng đối tượng (OOD). Nó là một ví dụ sai lầm nổi tiếng "Shape". Nó thường được dùng để miêu tả cách mà đa hình hoạt động. Tuy nhiên, chúng ta sẽ dùng nó ở đây để làm rõ OCP.

Chúng ta có một ứng dụng có thể vẽ hình tròn và hình vuông trên giao diện đồ họa cơ bản. Hình tròn và hình vuông cần được vẽ theo một thứ tự nhất định. Một danh sách những hình tròn và hình vuông sẽ được tạo ra theo một thứ tự thích hợp, và chương trình cần kiểm tra lần lượt danh sách đó và vẽ các hình thích hợp.

** Vi phạm OCP **

Trong C, sử dụng lập trình thủ tục sẽ không thỏa mãn OCP. Chúng ta có thể giải bài toán như đoạn code dưới đây. Ở đây chúng ta định nghĩa một tập các cấu trúc dữ liệu có khởi tạo như nhau nhưng sẽ khác nhau khi chạy chương trình. Thành phần đầu tiên của mỗi cấu trúc sẽ là một mã để phân biệt xem đó là hình vuông hay hình chữ nhật. Hàm DrawAllShapes duyệt một mảng các con trỏ đến cấu trúc dữ liệu này, kiểm tra mã hình sau đó gọi hàm thích hợp (DrawCircle hay DrawSquare).

// -- shape.h --
enum ShapeType {circle, square};

struct Shape
{
  ShapeType itsType;
}

// -- circle.h --
struct Circle
{
  ShapeType itsType;
  double itsRadius;
  Point itsCenter;
}

void DrawCircle(struct Circle*);

// -- square.h --
struct Square
{
  ShapeType itsType;
  double itsSide;
  Point itsTopLeft;
}

void DrawSquare(struct Square*);

// -- drawAllShapes.c --
typedef struct Shape *ShapePointer;

void DrawAllShapes(ShapePointer list[], int n)
{
  int i;
  for (i = 0; i < n; i++)
  {
    struct Shape* s = list[i];
	switch (s->itsType)
	{
	case square:
	  DrawSquare((Struct Square*) s);
	  break;
	case circle:
	  DrawCircle((Struct Circle*) s);
	  break;
	}
  }
}

Hàm DrawAllShapes không thỏa mãn OCP bởi nó không thể đóng với một loại hình mới. Nếu tôi muốn mở rộng hàm này để có thể vẽ một danh sách hình trong đó có cả hình tam giác, tôi sẽ phải thay đổi chính hàm này. Thực sự, tôi cần phải thay đổi hàm này để nó có thể chấp nhận bất cứ hình gì.

Đương nhiên chương trình trên là một chương trình rất đơn giản. Trong thực tế, câu lệnh switch trong hàm DrawAllShapes sẽ phải lặp đi lặp lại rất nhiều lần ở các hàm trong toàn ứng dụng, mỗi hàm sẽ có một công việc hơi khác nhau một chút. Đó có thể là hàm để kéo thả hình, mở rộng hình, di chuyển hình, xóa,... Việc thêm một hình cho ứng dụng loại này có nghĩa là sẽ phải săn tìm tất cả những nơi mới có câu lệnh switch, (hoặc có thể là if/else) và sau đó là thêm với hình mới.

Hơn nữa, chúng ta không chắc là các câu lệnh switch hay if/else sẽ được tổ chức giống như trong hàm DrawAllShapes. Trong thực tế, điều thường diễn ra là chúng ta sẽ kết hợp câu lệnh điều kiện của if với các toán tử logic, hoặc ghép các trường hợp của câu lệnh switch lại để "đơn giản hóa" phép toán logic của chúng ta. Trong một vài trường hợp, sẽ có những hàm làm việc với hình vuông giống hệt với hình tròn. Những hàm đó còn chả có câu lệnh switch hay if/else. Do vậy, vấn đề của việc tìm kiếm và hiểu tất cả những nơi mà hình mới cần thêm vào trở nên không đơn giản chút nào.

Tiếp theo, hành xem xét loại thay đổi mà chúng ta sẽ làm. Chúng ta cần thêm một thành viên cho kiểu dữ liệu enum ShapeType. Bởi tất cả hình sẽ phục thuộc vào kiểu dự liệu này, chúng ta sẽ phải biên dịch lại chúng từ đầu. Chúng ta cũng phải biên dịch lại tất cả các mô-đun có liên quan đến Shape.

Do vậy, chúng ta không những chỉ phải thay đổi câu lệnh switch hay if/else, mà còn phải thay đổi các tập tin nhị phân (thông qua quá trình biên dịch lại) của tất cả các mô-đun sử dụng cấu trúc dữ liệu Shape. Thay đổi tập tin nhị phân có nghĩa là thay đổi DLL, thư viện chia sẻ hay bất cứ thành phần nhị phân nào có liên quan. Hành động đơn giản là thêm một hình kéo theo hàng loạt thay đổi đến hệ thống từ mã nguồn cho đến các tập tin nhị phân. Rõ ràng, ảnh hưởng của việc thêm một hình là rất lớn.

** Thiết kế tồi.**

Cùng nhìn lại một lần nữa. Lời giải đưa ra ở trên là cứng nhắc (Rigid) bởi việc thêm hình tam giác làm cho Shape, Square, Circle, DrawAllShapes phải được biên dịch lại. Nó dễ vỡ (Fragile) bởi rất nhiều câu lệnh switch/case hoặc if/else khó để tìm kiếm cũng như sửa chữa đúng đắn. Nó bất động (Immobile) bởi bất cứ ai muốn tái sử dụng DrawAllShapes trong chương trình khác sẽ phải mang theo cả Square và Circle kể cả khi họ không cần nó. Do vậy, đoạn code trên đã có quá nhiều dấu hiệu của thiết kế tồi.

** Thỏa mãn OCP **

Đoạn code sau đây cung cấp lời giải cho bài toán hình tròn/ hình vuông thỏa mãn OCP. Trong trường hợp này, chúng ta tạo ra một lớp trừu tượng Shape. Lớp trừu tượng này có một hàm trừu tượng là Draw. Cả hai class Circle và Square đều được sinh ra từ class Shape.

// Lời giải OOD cho bài toán Square/Circle
class Shape
{
  public:
    virtual void Draw() const = 0;
};

class Square : public Shape
{
  public:
    virtual void Draw() const;
};

class Circle : public Shape
{
  public:
    virtual void Draw() const;
};

void DrawAllShapes(vector<Shape*>& list)
{
  vector<Shape*>::iterator i;
  for (i=list.begin(); i != list.end(); i++) {
    (*i)->Draw();
  }
}

Chú ý rằng nếu chúng ta muốn mở rộng hành vi của hàm DrawAllShapes để vẽ được hình khác, tất cả những gì chúng ta cần là tạo ra một class sinh từ Shape. Hàm DrawAllShapes không cần phải thay đổi. Do vậy hàm DrawAllShapes thỏa mãn OCP. Hành vi của nó có thể mở rộng mà không cần thay đổi nó. Thật sự, việc thêm class Triangle tuyệt đối không tạo ra bất cứ ảnh hưởng nào đến bất cứ mô-đun nào đã tạo ra. Rõ ràng một vài thành phần của hệ thống cần thay đổi để làm việc với class Triangle, nhưng tất cả những dòng code ở trên đều không cần thay đổi.

Trong thực tế, class Shape có thể có nhiều phương thức hơn. Tuy nhiên, việc thêm hình vào trong ứng dụng của chúng ta là rất đơn giản bởi tất cả những gì chúng ta cần là tạo thêm class thực hiện Shape. Chúng ta không cần phải dò tìm toàn ứng dụng xem chỗ nào cần thay đổi. Do vậy, đây là một lời giải không dễ vỡ (not Fragile).

Nó cũng không cứng nhắc (not Rigid). Không có mã nguồn nào cần thay đổi, và nếu không có ngoại lệ, thì cũng không có tập tin nhị phân nào bị thay đổi. Mô-đun tạo ra thực thể cho class mới thực hiện Shape cần thay đổi. Thông thường là ở main hoặc hàm mà main gọi tới, hoặc phương thức của đối tượng tạo ra bởi main.

Cuối cùng, đây là một lời giải không bất động (not Immobile). DrawAllShapes có thể tái sử dụng ở bất cứ ứng dụng nào mà không cần phải mang theo Square hay Circle. Do vậy, lời giải này không có dấu hiệu của bất cứ đặc tính nào của thiết kế tồi.

Lời giải này thỏa mãn OCP. Nó có thể thay đổi bằng cách thêm code mới, chứ không phải sửa code có sẵn. Do vậy, nó không gây ra các thay đổi ở những chương trình liên quan. Sự thay đổi duy nhất là việc thêm mô-đun và thay đổi liên quan đến main cho phép thực thể mới được tạo ra.

** OK, tôi đã nói dối **

Ví dụ trên là một ví dụ hoàn toàn có trật tự. Hãy xem xét điều gì xảy ra với DrawAllShapes nếu chúng ta quyết định tất cả các hình tròn cần được vẽ trước hình vuông. Hàm DrawAllShapes không thể đóng với những thay đổi như vậy. Để thực hiện thay đổi đó, bạn cần phải vào trong hàm DrawAllShapes, kiểm tra tất cả hình tròn, rồi mới đến hình vuông.

** Dự đoán và kiến trúc "tự nhiên" **

Liệu chúng ta đã dự đoán được kiểu thay đổi này và đưa ra một lớp trừu tượng bảo vệ chúng ta khỏi nó. Cách trừu tượng hóa đưa ra ở đoạn code trên chỉ làm chương ngại cho chúng ta với loại thay đổi này, hơn là một sự giúp đỡ. Bạn có thể bất ngờ. Nhưng cuối cùng, điều gì có thể tự nhiên hơn một lớp Shape làm cơ sở để Square và Circle sinh ra? Tại sao mô hình tự nhiên này lại không phải mô hình tốt nhất? Đáp án rõ ràng là mô hình sẽ KHÔNG tự nhiên trong hệ thống mà thứ tự quan trọng hơn kiểu hình dạng.

Nó đưa chúng ta đến một kết luận phiền phức. Một cách tổng quá, không cần biết mô-đun của bạn "đóng" như thế nào, sẽ luôn có một loại thay đổi biến nó thành không đóng. Không có mô hình nào tự nhiên trong mọi hoàn cảnh!

Bởi tính đóng không thể hoàn thiện được, nó cần được xử lý một cách chiến lược. Có nghĩa là, người thiết kế cần lựa chọn loại thay đổi so với cái có thể đóng thiết kế của họ. Anh ta cần dự đoàn hầu hết các thay đổi có thể xảy ra, và sau đó xây dựng kiến trúc trừu tượng để bảo vệ mình khỏi thay đổi đó.

Điều này cần nhiều kinh nghiệm của người thiết kế. Người thiết kế có kinh nghiệm hy vọng anh ta biết được người dùng và môi trường kinh doanh đủ để có thể dự đoán các loại thay đổi đến hệ thống. Sau đó, anh ta sử dụng OCP để đáp ứng thay đổi có tần suất cao nhất.

Đây không phải là điều đơn giản. Khi lập trình viên đoán đúng, họ thắng. Khi họ đoán sai, họ thua. Và họ thường đoán sai hầu hết các trường hợp.

Thêm vào đó, đáp ứng được OCP rất tốn kém. Nó tiêu tốn nhiều thời gian phát triển và nỗ lực để tạo ra một kiến trúc hợp lý. Tính trừu tượng cũng làm tăng lên độ phức tạp của ứng dụng. Có một lượng giới hạn sự trừu tượng mà lập trình viên có thể đáp ứng được. Rõ ràng, chúng ta cần giới hạn OCP cho một những thay đổi hay xảy ra nhất.

Làm cách nào chúng ta biết được thay đổi nào dễ xảy ra? Chúng ta cần nghiên cứu hợp lý, hỏi câu hỏi hợp lý, và dùng kinh nghiệm của mình cũng như những kiến thức chung. Và cuối cùng, chúng ta đợi đến khi thay đổi diễn ra!

** Cho "lưỡi câu" vào trong **

Làm cách nào chúng ta bảo vệ mình trước những thay đổi? Ở thế kỷ trước, chúng tôi có một câu nói. Chúng ta nên "cho lười câu vào trong" cho thay đổi mà chúng ta nghĩ là nó có thể xảy ra. Chúng tôi nghĩ rằng điều đó có thể giúp phần mềm trở nên mềm dẻo.

Tuy nhiên, lưỡi câu chúng tôi cho vào thường sai lầm. Sai lầm hơn nữa, nó lại có dấu hiệu của sự phức tạp không cần thiết (Needless Complexity) cần được hộ trợ vào bảo trì, kể cả khi chúng không được dùng đến. Đó không phải là một điều tốt. Chúng ta không muốn sử dụng một thiết kế có quá nhiều lớp trừu tượng. Thay vào đó, chúng ta thường đợi cho đến khi chúng ta thực sự cần trừu tượng hóa, rồi mới phát triển nó.

** Lừa gạt tôi một lần... **

Có một câu nói từ xa xưa: "Lừa tôi một lần, bạn xấu hổ. Lừa gạt tôi hai lần, tôi xấu hổ." Đây là một thái độ mạnh mẽ trong thiết kế phần mềm. Để ứng dụng của chúng ta thoát khỏi sự phức tạp không cần thiết (Needless Complexity), chúng ta có thể cho phép bản thân lừa mình một lần. Có nghĩa là chúng ta viết code và hy vọng sẽ không có thay đổi. Khi thay đổi xảy ra, chúng ta xây dựng lớp trừu tượng để bảo vệ mình khỏi những thay đổi trong tương lai có dạng đó. Nói ngắn gọn, chúng ta tóm viên đạn đầu tiên, và chắc chắn rằng mình sẽ được bảo vệ từ bất cứ viên đạn nào bắn ra từ cùng khẩu súng đó.

** Mô phỏng thay đổi **

Nếu chúng ta quyết định tóm viên đạn đầu tiên, chúng ta có lợi thế biết được hướng bay của viên đạn sớm hơn. Chúng ta biết được loại thay đổi có thể diễn ra trước khi chúng ta đi quá xa trong lộ trình phát triển. Chúng ta càng đợi lâu để thấy được thay đổi đó, chúng ta càng khó để tạo ra một lớp trừu tượng hợp lý.

Do vậy, chúng ta cần mô phỏng thay đổi. Chúng ta làm điều đó thông qua hàng loạt cuộc thỏa luận đưa ra ở chương 2.

Chúng ta viết kịch bản kiểm thử trước. Kiểm thử là một loại hình sử dụng hệ thống. Bằng cách viết kiểm thử trước, chúng ta buộc hệ thống trở nên có thể kiểm thử được (testable). Do vậy, thay đổi trong một hệ thống có thể kiểm thử sẽ không làm chúng ta quá bất ngờ sau đó. Chúng ta sẽ phải xây dựng lớp trừu tượng có thể kiểm thử được. Chúng ta sẽ thấy rằng rất nhiều trong số các lớp trừu tượng đó giúp ích chúng ta khi các thay đổi sau này diễn ra.
Chúng ta phát triển trên càng vòng đời ngắn. Vài ngày thay vì vài tuần.
Chúng ta phát triển các chức năng trước cơ sở hạ tầng, và thường xuyên cho các bên liên quan thấy các chức năng đã làm được.
Chúng ta phát triển các chức năng quan trọng nhất trước.
Chúng ta phân phối phần mềm nhanh và thường xuyên. Chúng ta đưa nó đến với khách hàng và người dùng nhanh chóng và thường xuyên nhất có thể.

** Sử dụng sự trừu tượng để đạt được tính đóng một cách minh bạch **

OK, vậy chúng ta đã tóm được viên đạn đầu tiên. Người dùng muốn vẽ hình tròn trước hình vuông. Giờ chúng ta phải bảo vệ bản thân khỏi những thay đổi có dạng này trong tương lai.

Làm cách nào để chúng ta đóng được hàm DrawAllShapes trước các thay đổi về thứ tự vẽ? Nhớ rằng tính đóng phụ thuộc vào sự trừu tượng. Do vậy, để đóng được hàm DrawAllShapes trước sự thay đổi, chúng ta cần sự trừu tượng về thứ tự. Loại trừu tượng này cung cấp một lớp có thể mô tả được thứ tự vẽ.

Mỗi quy tắc sắp xếp sẽ gồm hai đối tượng, để có thể xác định đối tượng nào được vẽ trước. Chúng ta có thể định nghĩa phương thức trừu tượng cho Shape tên là Precedes. Hàm này nhận một hình khác làm tham số và trả về giá trị luận lý (boolean). Kết quả là đúng (true) nếu đối tượng Shape nhận được thông báo cần được vẽ trước khi đối tượng Shape được truyền vào dưới dạng tham số.

Trong C++, phương thức có dạng này được biểu thị dưới dạng operator<. Đoạn code sau đây mô tả class Shape sẽ như thế nào khi có thêm phương thức sắp xếp.

// Shape with ordering method
class Shape
{
  public:
	virtual void Draw() const = 0;
	virtual bool Precedes(const Shape&) const = 0;

	bool operator<(const Shape& s) {return Precedes(s);}
}

Đến đây, chúng ta có thể xác định quan hệ sắp xếp giữa hai đối tượng Shape. Chúng ta có thể sắp xếp chúng rồi mới vẽ. Đoạn code sau viết bằng C++ sẽ thực hiện công việc đó.

// DrawAllShapes with Ordering
template <typename P>
class Lessp // utility for sorting container or pointers
{
  public:
    bool operator()(const P p, const P q) {return (*p) < (*q);}
}

void DrawAllShapes(vector<Shape*>& list)
{
  vector<Shape*> orderedList = list;
  sort(orderedList.begin(),
       orderedList.end(),
	   Lessp<Shape*>*());

  vector<Shape*>::const_iterator i;
  for (i=orderedList.begin(); i < orderedList.end(); i++)
	(*i)->Draw();
}

Bây giờ chúng ta có thể vẽ hình và vẽ theo thứ tự định sẵn. Tuy nhiên có vẻ chúng ta chưa có giải pháp cho việc vẽ theo thứ tự giảm dần mà bài toán yêu cầu. Do vậy, chúng ta cần sửa hàm Precedes của class Shape trong các lớp con để chỉ định thứ tự sắp xếp. Làm cách nào để thự hiện điều đó? Dòng code nào nên ghi ở Circle::Precedes để đảm bảo hình tròn sẽ được vẽ trước hình vuông? Xem xét đoạn code sau.

// Ordering a Circle
bool Circle::Precedes(const Shape& s) const
{
  if (dynamic_cast<Square*>(s))
    return true;
  else
    return false;
}

Rõ ràng ở phương thức trên, cũng như những người anh em của nó cùng sinh ra từ Shape, không thỏa mãn OCP. Không có cách nào để đóng chúng trước những lớp con mới của Shape. Mỗi khi có một lớp con được sinh ra, tất cả các hàm Precedes cần thay đổi.

Tất nhiên sẽ chẳng có vấn đề gì nếu không có thêm lớp con nào sinh ra từ Shape. Ngược lại, nếu chúng được tạo ra thường xuyên, thiết kế sẽ phải thay đổi rất nhiều. Vậy, một lần nữa, chúng ta lại bắt được viên đạn.

** Sử dụng cách tiếp cận định hướng từ dữ liệu để đạt được tính đóng **

Nếu chúng ta muốn đóng các con của Shape để chúng không cần biết các con khác, chúng ta có thể tiếp cận từ dữ liệu. Dưới đây là một giải pháp.

// Cơ chế quản lý sắp xếp sử dụng bảng
#include <typeinfo>
#include <string>
#include <iostream>

using namespace std;

class Shape
{
  public:
    virtual void Draw() const = 0;
	bool Precedes(const Shape&) const;
	bool operator<(const Shape& s) const {return Precedes(s);}
	static void const char* typeOrderTable[];
};

const char * Shape::typeOrderTable[] =
{
  typeid(Circle).name(),
  typeid(Square).name(),

};

// Hàm sau tìm kiếm bảng theo tên class.
// Bảng định nghĩa thứ tự mà các hình được vẽ.
// Hình không tìm được luôn được sắp xếp trước hình tìm được.
bool Shape::Precedes(const Shape& s) const
{
  const char* thisType = typeid(*this).name();
  const char* argType = typeid(s).name();
  bool done = false;
  int thisOrd = -1;
  int argOrd = -1;
  for (int i = 0; !done; i++) {
    const char* tableEntry = typeOrderTable[i];
	if (tableEntry != 0)
	{
	  if (strcmp(tableEntry, thisType) == 0)
	    thisOrd = i;
	  if (strcmp(tableEntry, argType) == 0)
	    argOrd = i;
	  if ((argOrd >= 0) && (thisOrd >= 0))
	    done = true;
	}
	else // table entry == 0
	  done = true;
  }

  return thisOrd < argOrd;
}

Bằng cách tiếp cận này, chúng ta đã thành công trong việc đóng hàm DrawAllShapes trước những thay đổi về thứ tự các hình, trong đó có việc thêm hình mới hoặc thay đổi thứ tự sẵn có (ví dụ vẽ hình vuông trước hình tròn).

Có duy nhất một thành phần không đóng trước những thay đổi về thứ tự là bảng của Shape. Bảng này có thể được đặt ở một mô-đun riêng của Shape, tách biệt với các mô-đun còn lại cho nên thay đổi ở đó không ảnh hưởng đến mô-đun khác. Thực tế, với C++, chúng ta có thể lựa chọn bảng nào sẽ sử dụng trong khi thiết lập liên kết.

Kết luận

Theo nhiều cách, OCP là trái tim của thiết kế hướng đối tượng. Thỏa mãn nguyên tắc này là điều tạo nên lợi ích lớn nhất từ kỹ thuật lập trình hướng đối tượng (tính mềm dẻo, tính tái sử dụng được, tính bảo trì,...). Tuy nhiên, thỏa mãn được nguyên lý này không đạt được một cách đơn giản bởi sử dụng ngôn ngữ lập trình hướng đối tượng. Cũng như không nên áp dụng hàng tá lớp trừu tượng cho tất cả các thành phần của ứng dụng. Thay vào đó, nó yêu cầu lập trình viên sử dụng tính trừu tượng cho những phần mà thường xuyên có thay đổi một cách rõ ràng. Chống lại sự trừu tượng ở dạng non nớt cũng quan trọng như bản thân sự trừu tượng.

Bạn đọc có thể tham khảo slide sau của tôi để có được cái nhìn tổng quát về 5 nguyên tắc thiết kế linh hoạt: http://www.slideshare.net/dinhhoanglong91/object-oriented-design-principle

Agile Design Pattern