Một số phương pháp làm mịn trong mô hình trong mô hình N-gram
Bài đăng này đã không được cập nhật trong 4 năm
Ngôn ngữ tự nhiên là những ngôn ngữ được con người sử dụng trong các giao tiếp hàng ngày: nghe, nói đọc, viết. Mặc dù con người có thể dễ dàng hiểu được và học các ngôn ngữ tự nhiên nhưng việc làm cho máy hiểu được ngôn ngữ tự nhiên không phải là chuyện dễ dàng. Sở dĩ có khó khăn là do ngôn ngữ tự nhiên có các bộ luật, cấu trúc ngữ pháp phong phú hơn nhiều các ngôn ngữ máy tính, hơn nữa để hiểu đúng nội dung các giao tiếp, văn bản trong ngôn ngữ tự nhiên cần phải nắm được ngữ cảnh của nội dung đó. Các phương pháp xử lý ngôn ngữ tự nhiên dựa trên thống kê không nhắm tới việc con người tự xây dựng mô hình ngữ pháp mà lập chương trình cho máy tính có thể “học” nhờ vào việc thống kê các từ và cụm từ có trong văn bản. Cốt lõi nhất của phương pháp xử lý ngôn ngữ tự nhiên dựa trên thống kê chính là việc xây dựng mô hình ngôn ngữ.
1. Khái quát về N-gram
- N-gram được hiểu đơn giản là tần suất xuất hiện của n kí tự (từ) liên tiếp xuất hiện trong dữ hiêu
- Một số mô hình n-gram phổ biến
- unigram, mô hình với n=1, tức là ta sẽ tính tần suất xuất hiện của một kí tự (từ), như: "k", "a",...
- bigram với n=2 , là mô hình được sử dụng nhiều trong việc phân tích các hình thái cho ngôn ngữ
- trigram với n-3, với n càng lớn thì độ chính xác càng cao tuy nhiên đi kèm với đó thì độ phức tạp cũng lớn hơn
- Để xây dựng một mô hình n-gram, ban đầu người ta dựa trên một tập dữ liệu huấn luyện( Tranning set). Sau khi mô hình được xây dựng, ta tiến hành kiểm tra mô hình dựa trên một tập dữ liệu test. Việc kiểm tra tốt nhất là sử dụng một tập dữ kiệu không có trong tập huấn luyện. Dựa vào việc kiểm tra này mà ta có thể biết được mô hình có tốt hay không
- Mô hình N-gram:
- Để tính xác suất của một câu: W1W2....Wk....Wn. Theo công thức Bayes ta sẽ tính bằng cách:
P(W1W2..Wk...Wn) = P(W1)*P(W2|W1)*...*P(Wk|W1...Wk-1)*...*P(Wn|W1....Wn) - Tuy nhiên, công thức trên có độ phức tạp lớn, vì vậy người ta thường sử dụng công thức Markov:
𝑃( W1 W2 … W𝑖 ) = 𝑃( W1 ) ∗ 𝑃( W2 |W1 ) ∗ 𝑃( W3 W1W2 ) ∗ … ∗ 𝑃( Wi-1 |Wi−𝑛−1 W𝑖−𝑛 W𝑖−2) ∗ 𝑃(W𝑖 |W𝑖−𝑛 W𝑖− 𝑛+1 W𝑖−1 )
- Để tính xác suất của một câu: W1W2....Wk....Wn. Theo công thức Bayes ta sẽ tính bằng cách:
- Do khi tính xác suất có nhiều trường hợp sẽ gặp các cụm n-gram chưa xuất hiện hoặc do sự phân bố không đều trong tập huấn luyện sẽ dẫn tới việc tính toán không chính xác. Vì vậy người ta đưa ra phương pháp làm mịn để khắc phục vấn đề này
- Các phương pháp làm mịn có thể chia thành 3 loại chính:
- Discounting: giảm xác suất các cụm n-gram có xác suất lớn hơn 0 để bù cho các cụm n-gram chưa xuất hiện
- Back-off: tính xác suất các cụm n-gram chưa xuất hiện bằng các cụm ngắn hơn và có xác suất lớn hơn 0
- Interpolation: tính xác suất của tất cả các cụm n-gram bằng các cụm ngắn hơn
2.Add-one(Laplace)
- Phương pháp này sẽ cộng thêm vào số lần xuất hiện của mỗi cụm n-gram lên 1, khi đó xác suất của cụm n-gram sẽ được tính lại là:
P = (C + 1)/ + (M + V)Trong đó, C là của số lần xuất hiện cụm n-gram trong tập ngữ liệu mẫu, N là số cụm n-gram, V là kích thước của toàn bộ từ vựng. - Ở đây,
∑ C = Nvì thế sau khi thêm 1 vào tần suất xuất hiện mỗi cụm n-gram, tổng này trở thành∑(C + 1) = N + V- Với Unigram, ta có thể viết lại công thức trên như sau,
P'=(C'+1)/(M+V) - Với n-gram(bigram, trigram,...), ta có
P'(Wi|W1W2...Wk-1)=(C(W1W2...Wk)+1)/ C(W1W2...Wk-1) + V
- Với Unigram, ta có thể viết lại công thức trên như sau,
- Tuy nhiên, để cân đối lại xác suất và tăng độ chính xác người ta thương thêm một hệ số λ(lamda) vào công thức. Khi đó ta có
P=(C+λ)/(M+λV)P'(Wi|W1W2...Wk-1)=(C(W1W2...Wk)+λ)/ C(W1W2...Wk-1) +λ V- Đặc biệt với λ=1/2, ta có phương pháp Jeffreys – Perks:P'(Wi|W1W2...Wk-1)=(C(W1W2...Wk)+ M/V)/ C(W1W2...Wk-1) +M
3.Good-Turing
- Để tránh một cụm n-gram có nghĩa nhưng lại có tần suất xuất hiện nhỏ, người ta sử dụng phương pháp làm mịn dựa trên ước lượng cùng tần suất, nghĩa là nhóm các cụm n-gram có số lần xuất hiện như nhau. Cách tính như sau:
- Với cụm n-gram chưa xuất hiện trước đó:
P=N1/N - Với cụm n-gram đã từng xuất hiện:
P=(c+1)*Nc+1/N*Nc-Trong đó, N1: Số cụm n-gram xuất hiện 1 lần, N : Tổng số cụm n-gram, c: số lần xuất hiện của cụm n-gram, Nc+1: Tổng số cụm n-gram xuất hiện c+1 lần
- Với cụm n-gram chưa xuất hiện trước đó:
- Ví dụ, trong tập huấn luyện ta có các từ với số lần xuất hiện như sau: sách: 10 lần, vở: 3 lần, phấn: 2 lần, bút: 1 lần, giấy: 1 lần, kéo: 1 lần. Tổng các từ là 18. Vậy xác suất để từ "tẩy" chưa có trong tập huấn luyện xuất hiện là: 3/18, xác suất để từ "giấy" xuất hiện là: 21/(318) = 3/27
4.Back-off
- Trong phương pháp Add-one hoặc Add-λ nếu cụm W1...Wk-1 và được cụm W1...Wk đều không xuất hiện trong tập huấn luyện, thì sau khi làm mịn xác suất vẫn là 0. Với phương pháp truy hồi (Back-off ) ta sẽ giải quyết được vấn đề này
- Back-off là một phương pháp mà xác suất được tính từ điều kiện của cụm n-gram trước đó. Nó được tính toán này bằng cách "backing-off" với cụm n-gram ngắn hơn đã có trong những điều kiện nhất định. Bằng cách đó, back-off có các xác suất tin cậy đã được tính để tạo ra các kết quả tốt hơn.
- Công thức:
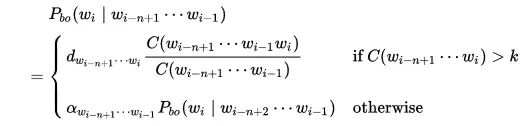
- Trong phương pháp Back-off sự chính xác của mô hình phụ thuộc nhiều vào tham số alpha. Có một vài cách để chọn alpha tùy theo tập huấn luyện và mô hình n-gram . Một cách đơn giản ta có thể chọn alpha là một hằng số. tuy nhiên rất khó để chọn được một hằng số để tổng xác suất các cụm n-gram không đổi. Việc chọn hằng số không chính xác sẽ ảnh hường lớn đến độ chính xác của mô hình. Ta có thể chọn alpha như một hàm của n-gram theo (Wk-1Wk). Tuy nhiên để mô hình có độ chính xác cao người ta thường kết hợp thêm một số phương pháp như Good-turing để làm giảm xác suất của các cụm n-gram đã xuất hiện.
5. Kneser-ney
- Kneser-Ney là phương pháp chủ yếu được sử dụng để tính toán phân bố xác suất của n-gram trong một tài liệu dựa trên những tính toán đã có.
- Kneser-Ney được coi là phương pháp hiệu quả nhất để làm mịn do việc sử dụng các chiết khấu tuyệt đối bằng cách trừ đi một giá trị cố định từ điều kiện về tần số bậc thấp của xác suất để bỏ qua n-gram với tần số thấp hơn. Đây là phương pháp hiệu quả với bigram và các mô hình n-gram cao hơn.
- Một ví dụ phổ biến để minh họa các khái niệm đằng sau phương pháp này là tần số Bigram cảu cụm "San Francisco". Nếu nó xuất hiện nhiều lần trong một ngữ liệu huấn luyện, tần số của unigram "Francisco" cũng sẽ cao. Dựa vào chỉ có tần số unigram để dự đoán các tần số của n-gram sẽ dẫn đến kết quả sai lệch. Tuy nhiên, Kneser-Ney mịn chỉnh này bằng cách xem xét các tần số của unigram liên quan đến những từ ở trước.
- Công thức Kneser-ney:
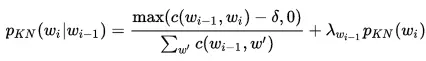
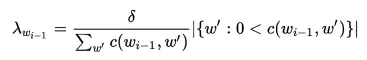
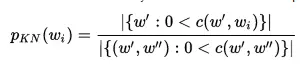
Mô hình n-gram hiện nay được ứng dụng vào rất nhiều trong xác suất, học máy, ngôn ngữ: kiểm tra chính tả, dự đoán từ,...
Tài liệu tham khảo
All rights reserved