Một trong những lí do mà Deep Learning ngày càng trở nên phổ biến trong những năm gần đây là những kĩ thuật, thuật toán giúp quá trình học của mô hình nhanh hơn và cho kết quả ngày càng tốt hơn. Cùng với sự xuất hiện của những kĩ thuật đó, một yếu tố quan trọng và xuất hiện trên tất cả các mô hình Deep Learning chính là các hàm kích hoạt (activation functions). Trong bài viết này mình sẽ giới thiệu cho mọi người về một số activation functions và tính chất của chúng, cũng như thảo luận về tâm quan trọng của chúng trong quá trình học của mạng neural.

Sơ lược về Deep Learning

Lý do chính làm các mô hình mạng neural nổi bật hơn so với các mô hình học máy là khả năng giải quyết được những vấn đề về tính chất phi tuyến của dữ liệu (non-linear separable data). Những tầng mạng nằm giữa tầng đầu vào và đầu ra của một mạng neural được gọi là tầng ẩn. Những tầng ẩn này giữ nhiệm vụ giải quyết những quan hệ phi tuyến phức tạp giữa các đặc điểm của dữ liệu và kết quả đầu ra của mô hình nhờ những hàm "phi tuyến hóa" thường được biến đến với tên "activation functions".

Tại sao các activation functions lại quan trọng đến vậy ?

Trước khi giới thiệu về các activation functions phổ biến, hãy cùng thảo luận xem lí do gì khiến các hàm này lại quan trọng với các mô hình mạng neural đến vậy. Activation functions là những hàm phi tuyến được áp dụng vào đầu ra của các nơ-ron trong tầng ẩn của một mô hình mạng, và được sử dụng làm input data cho tầng tiếp theo.

Hãy tưởng tượng chúng ta có một mạng FFNN đơn giản với 2 tầng ẩn (blue) và mỗi tầng ẩn có 3 sigmoid neurons (neurons có activation là hàm sigmoid). Chúng ta có 3 neurons ở tầng input và 1 neuron ở tầng output. Với mỗi neurons, trong tầng ẩn, có 2 sự tác động

1. Pre-activation (kí hiệu là "a"): Phép tính tuyến tính giữa neurons input, weights và biases
2. Activation (kí hiệu là "h"): Sự chuyển đổi phi tuyến kết quả đầu ra của neurons

Pre-activation step

Chuyện gì sẽ xảy ra nếu không có các hàm phi tuyến này ?

Hãy tưởng tượng rằng thay vì áp dụng 1 hàm phi tuyến, ta chỉ áp dụng 1 hàm tuyến tính vào đầu ra của mỗi neuron. Vì phép biến đổi không có tính chất phi tuyến, việc này không khác gì chúng ta thêm một tầng ẩn nữa vì phép biến đổi cũng chỉ đơn thuần là nhân đầu ra với các weights. Với chỉ những phép tính đơn thuần như vậy, trên thực tế mạng neural sẽ không thể phát hiện ra những quan hệ phức tạp của dữ liệu (ví dụ như: dự đoán chứng khoán, các bài toán xử lý ảnh hay các bài toán phát hiện ngữ nghĩa của các câu trong văn bản). Nói cách khác nếu không có các activation functions, khả năng dự đoán của mạng neural sẽ bị giới hạn và giảm đi rất nhiều, sự kết hợp của các activation functions giữa các tầng ẩn là để giúp mô hình học được các quan hệ phi tuyến phức tạp tiềm ẩn trong dữ liệu.

Một số activation functions phổ biến

Sigmoid function (Logistic Function)

Sigmoid function

Nếu bạn đã làm quen một vài mô hình học máy, chắc hẳn banj vẫn còn nhớ về Logistic Regression - một thuật toán phân loại nhị phân đơn giản mà khá hiệu quả. "Linh hồn" của Regression chính là hàm Sigmoid này. Sigmoid là một hàm phi tuyến với đầu vào là các số thực và cho kết quả nằm trong khoảng [0,1] và được xem là xác xuất trong một số bài toán. Trong hàm Sigmoid, một sự thay đổi nhỏ trong input dẫn đến một kết quả output ko mấy thay đổi. Vì vậy, nó đem lại một đầu ra "mượt" hơn và liên tục hơn so với input.

Công thức của hàm Sigmoid và đạo hàm của nó được nêu ra dưới đây: https://images.viblo.asia/9da3c8f2-ec39-44a7-b349-8c0804ba75e0.png Hàm sigmoid là một hàm liên tục và đạo hàm của nó cũng khá đơn giản, dẫn đến việc áp dụng hàm vào mô hình mạng đem lại sự dễ dàng trong việc xây dựng mô hình và cập nhật tham số dựa trên back-propagation. Một điểm đáng chú ý của hàm Sigmoid, khiến nó trở nên nổi bật trong thời gian gần đây lại là điểm "bất lợi" của nó. Chúng ta sẽ làm quen với khái niệm "Vanishing Gradient"

Vanishing Gradient - Saturated Sigmoid Neurons:

Một neuron có activation function là hàm sigmoid được xem như bão hòa (saturated) nếu nó đạt được giá trị lớn nhất, hoặc nhỏ nhất. Trong công thức toán học của hàm Sigmoid, khi ta để đầu vào là một số cực lớn (dương vô cùng), đầu ra của nó sẽ đạt giá trị rất gần 1, và ngược lại, giá trị của nó sẽ đạt 0 nếu ta đưa vào input 1 số cực bé (âm vô cùng).

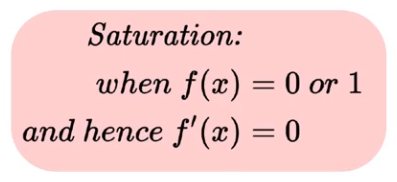
Khi hàm số đạt được giá trị cực tiểu hay cực đại, ta nói hàm số bão hòa. Do đó, đạo hàm của hàm Sigmoid trở thành 0 tại điểm bão hòa. Hãy cùng nhìn qua một ví dụ để thấy được ảnh hưởng của vấn đề về sự bão hòa của sigmoid neuron.

Trong mạng "nhỏ" nhưng "sâu" trên hình, giả sử bạn muốn tính đạo hàm của weight w2 của hàm loss. Pre-activation và post-activation của neuron trong tầng ẩn thứ 3 là:

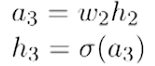
Và bạn đã tính toán rất cẩn thận đạo hàm theo "chain rule":

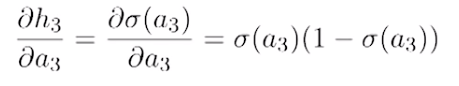
Nếu 'h3' đạt được giá trị rất gần với giá trị bão hòa, giá trị của đạo hàm sẽ là 0. Do đó sẽ không có sự cập nhật tham số nào ở đây cả. Đó là vanishing gradient problem. Từ đây ta có thể thấy được rằng, một neuron đạt trạng thái bão hòa sẽ khiến cho đạo hàm biến mất, và việc cập nhật trọng số sẽ bị ảnh hưởng rất nhiều.

Tại sao hàm sigmoid lại bão hòa trong mô hình ?

Ta đã thấy vấn đề khi hàm đạt giá trị bão hòa nhưng tại sao và khi nào thì nó bão hòa ? Nếu đầu vào của hàm là một số cực lớn hoặc cực bé (điều này có nghĩa là input và weights đều phải là những số có tính chất tương tự) nó có thể dẫn đến sự bão hòa. Chúng ta biết rằng trước khi đưa dữ liệu vào mô hình mạng, dữ liệu hầu hết được tiền xử lý bằng cách chuẩn hóa các giá trị về miền [0,1], điều này có thể giảm thiểu được khả năng trên. Ngoài ra, khi khởi tạo weights cho mô hình chúng ta cũng nên tránh những giá trị quá lớn vì nó cũng có thể dẫn đến việc hàm sigmoid bị bão hòa.

Hàm sigmoid không có tính chất Zero-centered !

Do điểm bão hòa của hàm số là 1 và 0 nên ta có thể dễ dàng nhận thấy được trung bình của hàm không phải là 0. Một "zero-centered function" có tính chất lấy 0 làm trung tâm miền giá trị, có nghĩa là giá trị của nó sẽ có thể lớn hơn và nhỏ hơn 0.

Hãy cũng xem xét vấn đề mà điều này đem lại qua một ví dụ nhỏ dưới đây. Xét 2 tầng cuối trong mạng. Trạng thái "pre-activation" của tầng gần cuối là "a3".

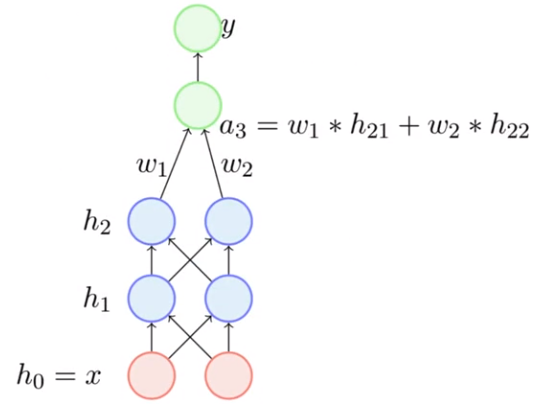
Hãy thử tính toán đạo hàm của loss đối với w1 và w2:

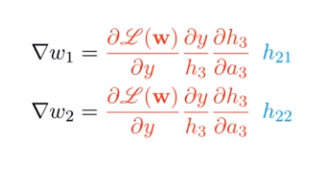
Nhớ rằng h21 và h22 là output của sigmoid function vì vậy giá trị của chúng luôn > 0. Vì vậy dấu của đạo hàm sẽ cùng dấu với phần được tô đỏ, do đó việc cập nhật giữa các weights luôn cùng là dương, hoặc luôn cùng là âm. Do đó, việc cập nhật sẽ chỉ diễn ra theo 1 số hướng nhất định, hạn chế sự linh hoạt của mô hình.

Conclusion

Trong bài viết mình đã thảo luận về tác dụng cũng như giới thiệu và đưa ra những thảo luận xoay quanh một activation function là hàm sigmoid. Hàm số tưởng chừng như đơn giản nhưng nếu không để ý khi sử dụng có thể dẫn đến những kết quả không mong muốn. Trong phần tới mình sẽ giới thiệu thêm cho các bạn về các hàm activation khác và những vấn đề liên quan. Hãy đón đọc nhé !

References