ML From Scratch: Thuật toán phân loại Naive Bayes - Viblo

Bài đăng này đã không được cập nhật trong 2 năm

Chào mọi người, trong Series Machine Learning From Scratch này mình và các bạn sẽ cùng đi triển khai các thuật toán cơ bản trong học máy để cùng hiểu rõ hơn bản chất của các thuật toán này nhé.

1. Lý thuyết về định lý Bayes

Trên đây là công thức xác suất điều kiện, được sử dụng khi tính xác xuất xảy ra biến cố phụ thuộc vào biến cố đã xảy ra. Ví dụ: Xác xuất bạn Rưả chén nó sẽ khác với xác suất bạn Rửa chén khi có bố mẹ ở nhà, và khác với xác suất bạn rứa chén khi không có mẹ ở nhà. Khi đó, để phù hợp với công thức trên thì A là biến cố bạn rửa chén, B là biến cố mẹ bạn có ở nhà thì công thức trên thể hiện cho xác xuất bạn rửa chén khi mẹ có ở nhà, cụ thể nó sẽ phụ thuộc vào:

P(B): Xác xuất mẹ ở nhà
P(B|A) Xác xuất mẹ ở nhà khi bạn rửa chén
P(A): Xác suất bạn rửa chén

Còn đây là định lý Bayes được sử dụng trong thuật toán phân loại. Khi sử dụng công thức này để phân lớp chúng ta giả sử các thuộc tính phân lớp độc lập với nhau (Chỉ là giả sử thôi còn trong thực tế hơi khó). Biến cố dữ liệu đầu vào thuộc về một lớp nào đó trong n lớp được xem là một hệ đầy đủ ( $B_1$ , $B_2$ , ..., $B_n$ ). A là biến cố một dữ liệu nào đó cần dữ đoán, vậy để phân loại một dữ liệu nào đó cùng đồng nghĩa với việc tính P( $B_k$ , A) với k=1, 2, ...n và dữ liệu A sẽ thuộc vào lớp có xác suất cao nhất vừa tìm được. Lưu ý: Biến cố A là một điểm dữ liệu cần dự đoán, vậy nên sẽ A có thể có nhiều thuộc tính và vì các thuộc tính này độc lập (giả sử ở trên) nên sẽ được tính theo công thức nhân dưới đây.

2. Ví dụ

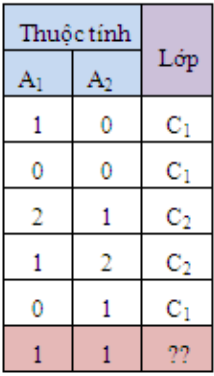
Với dữ liệu trên mình cần dự đoán nhãn C1 hay C2 cho điểm dữ liệu X( $A_1$ =1, $A_2$ =1). Mình sẽ đi tính các xác suất thành phần của công thức ở trên trước khi tính P( $C_1$ | X) và P( $C_2$ | X)

P( $C_1$ ) = 3/5 = 0.6
P( $C_2$ ) = 2/5 = 0.4
P(X | $C_1$ ) = P( $A_1$ =1| $C_1$ )*P( $A_2$ =1| $C_1$ ) = 1/3 * 1/3 = 1/9
P(X | $C_2$ ) = P( $A_1$ =1| $C_2$ )*P( $A_2$ =1| $C_2$ ) = 1/2 * 1/2 = 0.25

Cuối cùng là 2 xác xuất quan trọng nhất để so sánh (folllow theo đúng như công thức Bayes):

P( $C_1$ | X) = $\frac{P(C_1).P(X|C_1)}{P(X|C_1).P(C_1) + P(X|C_2).P(C_2)}$ = 0.4
P( $C_2$ | X) = $\frac{P(C_2).P(X|C_2)}{P(X|C_1).P(C_1) + P(X|C_2).P(C_2)}$ = 0.6

Vậy điểm dữ liệu X( $A_1$ =1, $A_2$ =1) thuộc lớp $C_2$

Lưu ý: Để phân lớp chúng ta chỉ cần tính phần tử số và so sánh vì phần mẫu số là giống nhau. Tuy nhiên ở đây mình vẫn tính đầy đủ để thể hiện biến cố dữ liệu thuộc về từng lớp là hệ đầy đủ nên sẽ có tổng bằng 1.

3. Code python

Ok sau khi hiểu lý thuyết chúng ta sẽ cùng đi implement thuật toán phân lớp Naive Bayes bằng ngôn ngữ python nhé Đầu tiên chúng ta sẽ đi khởi tạo dữ liệu như bảng trên

X = np.array([
    [1, 0],
    [0, 0],
    [2, 1],
    [1, 2],
    [0, 1],
])

y = np.array(["C1", "C1", "C2", "C2", "C1"])

Đều tiên là hàm tính xác xuất của lớp P( $C_1$ ) và P( $C_2$ ). Hàm này đơn giản là đếm số lần xuất hiện của lớp đó tỏng tập dữ liệu.

def get_class_prob(y: np.array):
  prob = {}
  n = len(y)
  for c in np.unique(y):
    prob[c] = np.count_nonzero(y == c) / n
  return prob

get_class_prob(y)

# output {'C1': 0.6, 'C2': 0.4}

Tiếp theo là hàm tính xác suất của tập thuộc tính theo điều kiện là các lớp để tính P(X | $C_2$ ), P(X | $C_2$ )

def get_condition_prob(X: np.ndarray, y: np.array, record: np.array):
  prob = {}
  for c in np.unique(y):
    # Lay tat ca record co class Ci
    class_records = X[y == c]
    n = class_records.shape[0]
    # Tinh xac xuat cua diem du lieu trong lop Ci theo cong thuc nhan
    prob[c] = np.prod(np.count_nonzero(class_records == record, axis=0)/n)
  return prob

input = np.array([1, 1])
get_condition_prob(X, y, input)

# output: {'C1': 0.1111111111111111, 'C2': 0.25}

Hàm này sẽ trả về xác xuất điều kiện của record đầu vào theoc các lớp có trong tập dữ liệu. Đầu tiên tại dòng 5, chúng ta sẽ lấy các dữ liệu theo điều kiện là lớp hiện tại đang tính. Sau đó tại dòng 8, chúng ta sẽ tìm số lần xuất hiện của các thuộc tính có trong record (np.count_nonzero), từ đó tính xác xuất (/n) và tích của chúng để được kêt quả (np.prod)

Và cuối dùng là xây dự hàm để dự đoán cho một điểm dữ liệu

def predict(X: np.ndarray, y: np.array, record: np.array):
  class_prob = get_class_prob(y)
  condition_prob = get_condition_prob(X, y, record)
  prob = {}
  for c in np.unique(y):
    prob[c] = (class_prob[c]*condition_prob[c])/ np.sum([class_prob[ci]*condition_prob[ci] for ci in class_prob])
  return prob

input = np.array([1, 1])
predict(X, y, input)

#output: {'C1': 0.39999999999999997, 'C2': 0.6}

Hàm này tính xác xuất điểm dữ liệu đầu vào thuộc về mỗi lớp dựa vào công thức ở trên, từ đó có thể đưa ra quyết định điểm dữ liệu đó thuộc vào lớp nào.

Và đây là full code:

import numpy as np

def get_class_prob(y: np.array):
  prob = {}
  n = len(y)
  for c in np.unique(y):
    prob[c] = np.count_nonzero(y == c) / n
  return prob

def get_condition_prob(X: np.ndarray, y: np.array, record: np.array):
  prob = {}
  for c in np.unique(y):
    # Lay tat ca record co class Ci
    class_records = X[y == c]
    n = class_records.shape[0]
    # Tinh xac xuat cua diem du lieu trong lop Ci theo cong thuc nhan
    prob[c] = np.prod(np.count_nonzero(class_records == record, axis=0)/n)
  return prob

def predict(X: np.ndarray, y: np.array, record: np.array):
  class_prob = get_class_prob(y)
  condition_prob = get_condition_prob(X, y, record)
  prob = {}
  for c in np.unique(y):
    prob[c] = (class_prob[c]*condition_prob[c])/ np.sum([class_prob[ci]*condition_prob[ci] for ci in class_prob])
  return prob

if __name__ == "__main__":
  X = np.array([
    [1, 0],
    [0, 0],
    [2, 1],
    [1, 2],
    [0, 1],
  ])

  y = np.array(["C1", "C1", "C2", "C2", "C1"])
  input = np.array([1, 1])
  result = predict(X, y, input)
  print(result)

4. Kết luận

Trong bài viết này mình và các bạn đã cùng tìm hiểu qua về cách mà thuật toán Naive Bayes hoạt động trong bài toán phân loại. Tuy nhiên, để có thể xây dựng một chương trình hoàn thiện để phân loại cần phải tối ưu hóa và chỉnh sửa rất nhiều thứ như tối ưu tốc độ chạy của code, xử lý các trường hợp đặc biệt (Ví dụ với công thức ở trên nếu có một xác xuất điều kiện của thuộc tính theo lớp bằng 0 thì dẫn đến xác xuất cuối cùng củng sẽ bằng 0, các bạn có thể tham khảo các giải quyết ở đây) Cuối cùng, cảm ơn các bạn đã đọc bài viết và nhớ Upvote cho mình nếu thấy bài viết hữu ích nhé.😀

AI Machine Learning classifier

1. Lý thuyết về định lý Bayes

2. Ví dụ

3. Code python

4. Kết luận

Mục lục