Matrix Factorization: Phương pháp gợi ý dựa trên kỹ thuật phân rã ma trận (P1)

Với mục tiêu hoàn thành loạt bài về Recommendation trước khi hết năm, Matrix Factorization là thuật toán cuối cùng về Recommendation mà mình muốn chia sẻ với các bạn. Cùng mình tìm hiểu nhé

1. Khái niệm

Matrix Factorization là một hướng tiếp cận khác của Collaborative Filtering, còn gọi là Matrix Decomposition, nghĩa là gợi ý bằng "kỹ thuật phân rã ma trận".

Kỹ thuật phân rã ma trận là phương pháp chia một ma trận lớn X thành hai ma trận có kích thước nhỏ hơn là W và H, sao cho ta có thể xây dựng lại X từ hai ma trận nhỏ hơn này càng chính xác càng tốt, nghĩa là X ~ $WH^T$

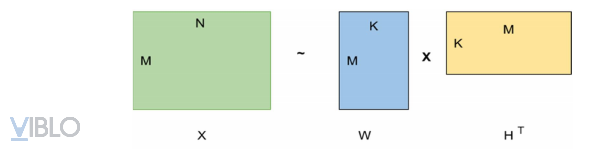
Có thể hiểu rằng, ý tưởng chính của Matrix Factorization là đặt items và users vào trong cùng một không gian thuộc tính ẩn. Trong đó, W ∈ $R^{\lvert{U}\lvert{}*K}$ là một ma trận mà mỗi dòng u là một vector bao gồm K nhân tố tiềm ẩn (latent factors) mô tả user u và H ∈ $R^{\lvert{}I\lvert{}*K}$ là một ma trận mà mỗi dòng i là một vector bao gồm K nhân tố tiềm ẩn mô tả cho item i.

Áp dụng phương pháp này vào bài toán gợi ý, chúng ta có x là một vector của item profile.

Mục tiêu của chúng ta là tìm một vector w tương ứng với mỗi user sao cho ratings đã biết của user đó cho item (y) xấp xỉ với:

Mở rộng với Y là utility matrix, giả sử đã được điền hết giá trị, ta có:

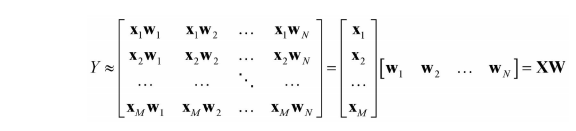
với M, N lần lượt là số users và số items.

Lưu ý, do X là được xây dựng dựa trên thông tin mô tả item và quá trình xây dựng này độc lập với quá trình đi tìm hệ số phù hợp cho mỗi user nên việc xây dựng item profile đóng vai trò quan trọng và có thể ảnh hưởng trực tiếp đến hiệu năng của mô hình. Thêm nữa, việc xây dựng mô hình riêng lẻ cho mỗi user dẫn đến kết quả chưa thực sự tốt vì không khai thác được đặc điểm giống nhau giữa các user.

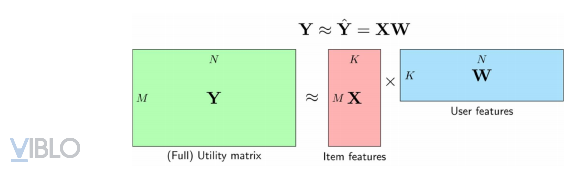
Giả sử rằng ta không cần xây dựng trước các item profile mà ma trận này có thể huấn luyện đồng thời với ma trận trọng số, hay nói các khác bài toán này là bài toán tối ưu các ma trận X và W, trong đó X là ma trận của toàn bộ các item profiles, mỗi hàng tương ứng với 1 item. Còn W là ma trận của toàn bộ user models (các mô hình của users), mỗi cột tương ứng với một user. Chúng ta sẽ cố gắng xấp xỉ utility matrix Y ∈ $R^{M*N}$ bằng tích của hai ma trận con là X ∈ $R^{M*K}$ và W ∈ $R^{K*N}$.

Trong đó, K được chọn thường nhỏ hơn rất nhiều so với M và N, và cả hai ma trận X và W đều phải có bậc (rank) không được vượt quá K

2. Xây dựng và tối ưu hàm mất mát

Cụ thể, quy trình xây dựng và tối ưu hàm mất mát như sau:

2.1. Hàm mất mát

Đầu tiên, chúng ta sẽ xét hàm mất mát không có cả bias và biến tối ưu cho X và W:

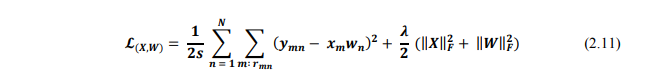
Trong đó, $r_{mn}$= 1 nếu item thứ m đã được đánh giá bởi user thứ n, ‖○‖ là căn bậc hai của tổng bình phương tất cả các phần tử của ma trận, s là toàn bộ số ratings đã có. Thành phần thứ nhất chính là trung bình sai số của mô hình. Thành phần thứ hai trong hàm mất mát phía, có tách dụng giúp tránh overfitting.

Lưu ý, tương tự như NBCF, các giá trị ratings được sử dụng là các giá trị đã chuẩn hóa, bằng cách trừ đi trung bình cộng các giá trị ratings đã biết trong cùng một hàng (với iiCF) và trong cùng một cột (với uuCF) – bài trước. Trong một số trường hợp, ta có thể không cần chuẩn hóa ma trận utility matrix nhưng những trường hợp đó sẽ phải dùng các kĩ thuật khác để giải quyết tính cá nhân trong các ratings.

Tiếp theo, chúng ta sẽ tối ưu X và W bằng cách cố định từng ma trận và tối ưu ma trận còn lại cho tới khi hội tụ.

2.2. Tối ưu hàm mất mát

Khi cố định X, việc tối ưu W chính là bài toán tối ưu của Content-based Filtering:

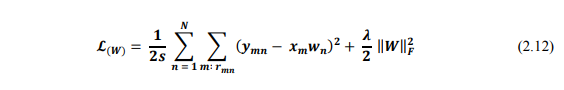
Ngược lại, khi cố định W, việc tối ưu X được đưa về tối ưu hàm:

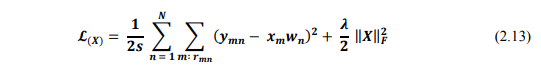
Hai bài toán này sẽ được tối ưu bằng Gradient Descent.

Chúng ta có thể thấy rằng, bài toán tối ưu W có thể được tách thành N bài toán nhỏ (N là số lượng users), mỗi bài toán tương ứng với việc đi tối ưu một cột của ma trận W.

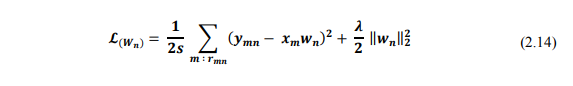
Vì biểu thức $(y_{mn} - x_mw_n)^2$ chỉ phụ thuộc vào các items đã được user đang xét đánh giá, nên ta có thể đơn giản nó bằng cách sử dụng sub matrix, là matrix chỉ chứa các giá trị ratings đã biết. Khi đó, hàm mất mát có dạng:

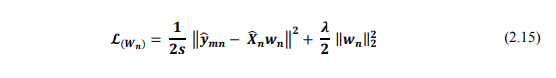
Và đạo hàm của nó là:

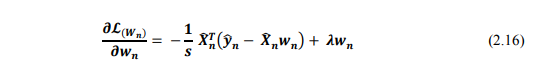
Vậy công thức cập nhật cho các cột của W là:

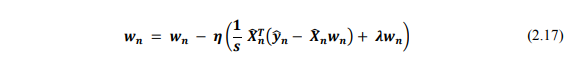
Tương tự với X, mỗi hàng tương ứng với một item sẽ được tìm bằng cách tối ưu:

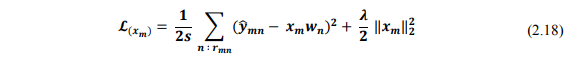
Đặt $W_m$ là ma trận được tạo bằng các cột của W tương ứng với các users đã đánh giá items đó và sử dụng submatrix Y tương ứng là $y_m$. Công thức trên sẽ trở thành:

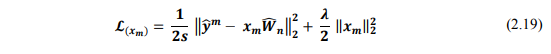
Vậy công thức cập nhật cho mỗi hàng của X là:

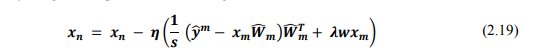
Sau khi cố định X, tính W và ngược lại, cố định W và tính X cho đến khi các ma trận này hội tụ, ta sẽ thu được ma trận X và W cần tìm. Từ đó, dự đoán các giá trị ratings chưa biết.

Ngoài phương pháp trên, để tăng độ chính xác của thuật toán này, ta sẽ xét hàm mất mát với bias và hệ số tối ưu cho X và W.

Như trong NBCF, chúng ta có bước chuẩn hóa ma trận để tránh sự thiên lệch do sự khó ttính hay dễ tính khác nhau giữa các users. Với MF, ta có thể chuẩn không chuẩn hóa mà sử dụng trực tiếp các giá trị ratings ban đầu, bằng cách tối ưu các biases cùng lúc với X và W.

Trong trường hợp này, ratings của user m cho item n được xác định bởi công thức:

với $b_m, d_n,\mu$ lần lượt là bias của item m, user n và ratings là ratings trung bình của toàn bộ các ratings.

Và hàm mất mát trong trường hợp này có dạng:

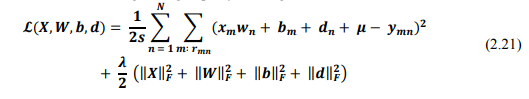
Tiến hành cố định X, b và tối ưu W, d và ngược lại, cố định W, d và tối ưu X, b, theo các công thức:

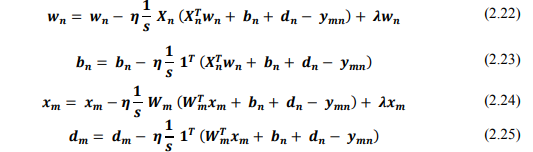
Cuối cùng, ta sẽ thu được các ma trận X, b, W, d, từ đó dự đoán các ratings chưa biết.

Trên đây là những lý thuyết căn bản về Matrix Factorization. Trong bài cuối của series này, mình sẽ viết demo cụ thể cho phương pháp này. Hi vọng bài viết của mình có ịch với bạn. Hẹn gặp lại trong những bài viết tiếp theo.

Tài liệu tham khảo:

Matrix Factorization Collaborative Filtering

Matrix Factorization techniques for recommender systems