Đã đăng vào Thứ Sáu, 2:03 CH 22 phút đọc

Mạng Nơ-ron Tích chập (Convolutional Neural Network - CNN)

Cơ sở lý thuyết và ứng dụng thực tiễn của mạng nơ-ron tích chập (CNN)

1. Tổng quan

Trong kỷ nguyên số hóa hiện đại, Thị giác Máy tính (Computer Vision) đã trở thành một trong những lĩnh vực nghiên cứu sôi động và có tính ứng dụng cao nhất của Trí tuệ Nhân tạo (AI). Từ xe tự hành, chẩn đoán y tế qua hình ảnh đến các hệ thống giám sát an ninh thông minh, khả năng "nhìn" và "hiểu" thế giới của máy tính phụ thuộc cốt lõi vào các mô hình học sâu (Deep Learning). Trong số đó, Mạng Nơ-ron Tích chập (Convolutional Neural Networks - CNN) đóng vai trò là kiến trúc nền tảng, tạo ra cuộc cách mạng về hiệu suất nhận dạng so với các phương pháp truyền thống.

Báo cáo này được xây dựng với mục tiêu cung cấp một tài liệu tham khảo toàn diện, chuyên sâu cấp độ đại học và sau đại học, phục vụ cho việc giảng dạy và nghiên cứu về CNN tại Việt Nam. Nội dung báo cáo tổng hợp các kiến thức hàn lâm từ các giáo trình danh tiếng thế giới như CS231n của Đại học Stanford, kết hợp với thực tiễn đào tạo tại các trường đại học hàng đầu Việt Nam như Đại học Bách Khoa Hà Nội (HUST), Đại học Quốc gia TP.HCM (VNU-HCM), và VinUniversity.

Báo cáo được cấu trúc thành ba phần chính, đi từ lý thuyết toán học cốt lõi đến triển khai thực tế trên hai bộ dữ liệu kinh điển: MNIST (nhận dạng chữ số viết tay) và Fashion-MNIST (phân loại thời trang), qua đó làm nổi bật sự tiến hóa trong tư duy thiết kế mô hình.

2. Phần I: Cơ sở Lý thuyết và Toán học của Mạng Nơ-ron Tích chập (CNN)

2.1. Động lực Sinh học và Sự ra đời của CNN

2.1.1. Từ Vỏ não thị giác đến Mô hình Toán học

Trước khi đi sâu vào các công thức toán học, điều quan trọng là phải hiểu nguồn gốc sinh học của CNN để nắm bắt triết lý thiết kế của nó. CNN không phải là một cấu trúc ngẫu nhiên mà là sự mô phỏng cơ chế hoạt động của vỏ não thị giác (visual cortex) ở động vật có vú, dựa trên những khám phá đoạt giải Nobel của Hubel và Wiesel vào thập niên 1950 và 1960.¹

Nghiên cứu của Hubel và Wiesel trên mèo cho thấy vỏ não thị giác có cấu trúc phân cấp. Các tế bào thần kinh (neuron) ở giai đoạn đầu (tế bào đơn giản - simple cells) chỉ phản ứng với các kích thích thị giác cụ thể trong một vùng không gian hẹp, gọi là trường tiếp nhận (receptive field), chẳng hạn như các cạnh định hướng (oriented edges) hoặc các thanh sáng tối. Thông tin từ các tế bào đơn giản này sau đó được tổng hợp bởi các tế bào phức tạp (complex cells) để nhận diện các mẫu hình lớn hơn và trừu tượng hơn, đồng thời tạo ra tính bất biến đối với các dịch chuyển nhỏ của vật thể trong không gian.³

Sự phân cấp này – từ việc phát hiện cạnh cục bộ đến việc nhận diện hình dạng tổng thể – chính là linh hồn của kiến trúc CNN. Khác với Mạng Nơ-ron Kết nối Đầy đủ (Fully Connected Network - MLP) hay mạng nơ-ron truyền thống, nơi mỗi neuron kết nối với tất cả các đầu vào, CNN áp dụng cơ chế kết nối cục bộ (local connectivity) và chia sẻ trọng số (parameter sharing), mô phỏng lại trường tiếp nhận sinh học.⁵

2.1.2. Hạn chế của Mạng Nơ-ron Truyền thống (MLP) với Dữ liệu Hình ảnh

Để hiểu tại sao CNN là cần thiết, ta cần xem xét sự thất bại của MLP khi xử lý ảnh. Một bức ảnh kỹ thuật số là một lưới các pixel. Ví dụ, một bức ảnh màu nhỏ có kích thước $200 \times 200$ pixel thực chất là một tensor 3 chiều với kích thước $200 \times 200 \times 3$ (chiều rộng, chiều cao, kênh màu RGB), tổng cộng chứa 120.000 giá trị số.²

Nếu ta sử dụng một mạng MLP truyền thống, ta phải duỗi phẳng (flatten) bức ảnh này thành một vector dài 240.000 phần tử (bao gồm cả 3 kênh). Giả sử lớp ẩn đầu tiên của mạng chỉ có 1.000 neuron, số lượng trọng số (weights) cần huấn luyện cho lớp này sẽ là:

$240000 \times 1000 = 240000000 \text{ tham số}$

Con số 240 triệu tham số chỉ cho lớp đầu tiên là quá lớn, dẫn đến hai vấn đề nghiêm trọng:

1. Chi phí tính toán khổng lồ: Việc huấn luyện trở nên bất khả thi trên phần cứng thông thường.

2. Quá khớp (Overfitting): Với số lượng tham số lớn hơn nhiều so với số lượng mẫu dữ liệu huấn luyện, mạng sẽ "ghi nhớ" từng ảnh thay vì học các đặc trưng chung, dẫn đến khả năng tổng quát hóa kém trên dữ liệu mới.¹

Hơn nữa, việc duỗi phẳng ảnh làm phá vỡ cấu trúc không gian (spatial structure). Trong một bức ảnh, mối quan hệ giữa một pixel và các pixel lân cận (trên, dưới, trái, phải) mang thông tin quan trọng về hình dạng và kết cấu. MLP coi pixel ở góc $(0,0)$ và pixel ở $(0,1)$ là hai đặc trưng độc lập không khác gì pixel ở $(200,200)$ , từ đó đánh mất thông tin topo học quý giá.⁷

2.2. Phép Tích chập (Convolution Operation)

2.2.1. Định nghĩa và Cơ chế Trượt

Trong bối cảnh xử lý ảnh và Deep Learning, thuật ngữ "tích chập" (convolution) thường được dùng để chỉ phép toán "tương quan chéo" (cross-correlation). Về mặt toán học thuần túy, tích chập yêu cầu lật ngược bộ lọc (kernel/filter) trước khi trượt, nhưng trong CNN, do các trọng số của bộ lọc được học từ dữ liệu, việc lật hay không lật không ảnh hưởng đến khả năng biểu diễn của mạng.⁸

Phép tích chập hoạt động bằng cách trượt một bộ lọc nhỏ (ví dụ $3 \times 3$ hoặc $5 \times 5$ ) qua toàn bộ hình ảnh đầu vào. Tại mỗi vị trí, một phép tính tổng các tích (sum of products) được thực hiện giữa các phần tử của bộ lọc và vùng ảnh tương ứng (được gọi là vùng cục bộ hay trường tiếp nhận).

Cho ảnh đầu vào $I$ có kích thước $H \times W$ và bộ lọc $K$ có kích thước $k_h \times k_w$ . Giá trị của bản đồ đặc trưng (feature map) đầu ra $S$ tại vị trí $(i, j)$ được tính bởi công thức:

$S(i, j) = (I * K)(i, j) = \sum_{m=0}^{k_h-1} \sum_{n=0}^{k_w-1} I(i+m, j+n) \cdot K(m, n) + b$

Trong đó $b$ là hệ số chệch (bias), là một tham số học được cộng thêm vào kết quả sau tích chập. Quá trình này được lặp lại cho tất cả các vị trí $(i, j)$ có thể trên ảnh đầu vào, tạo ra một bản đồ đặc trưng 2D. Bản đồ này đại diện cho "phản ứng" của bộ lọc đối với các vùng khác nhau của ảnh. Nếu bộ lọc là một bộ phát hiện cạnh dọc, bản đồ đặc trưng sẽ có giá trị cao tại các vùng có cạnh dọc trong ảnh gốc.²

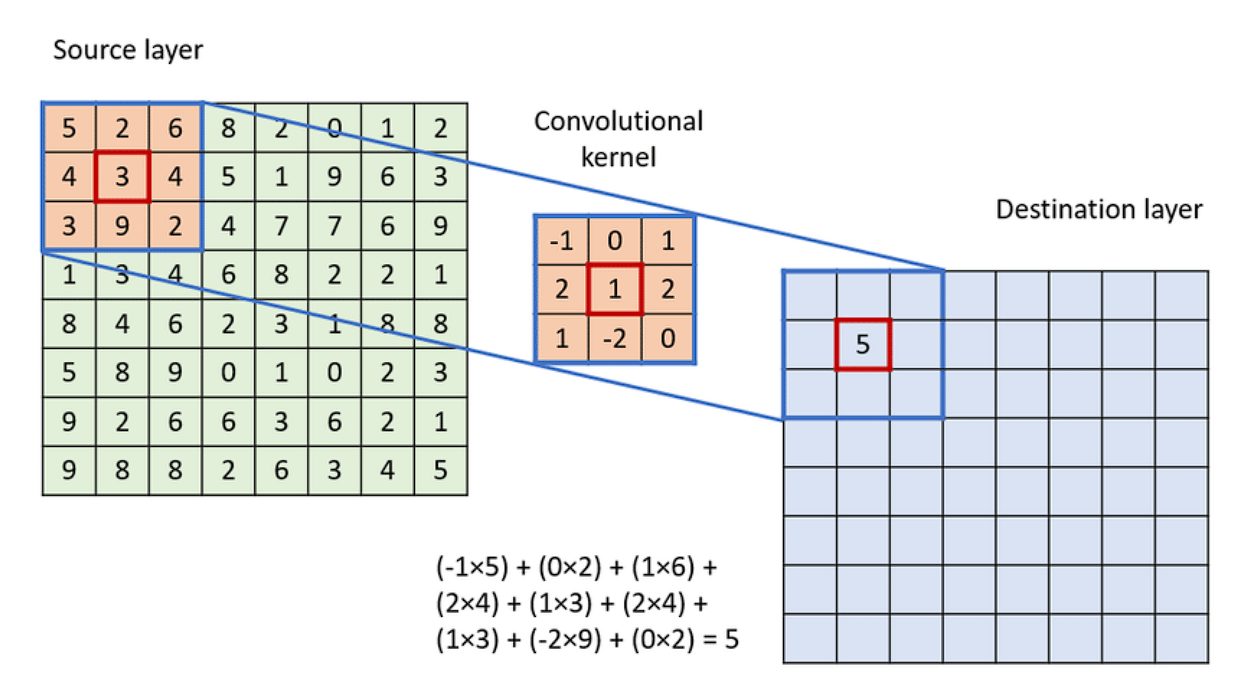
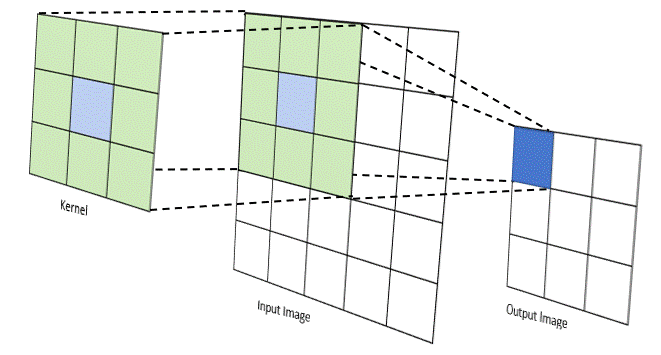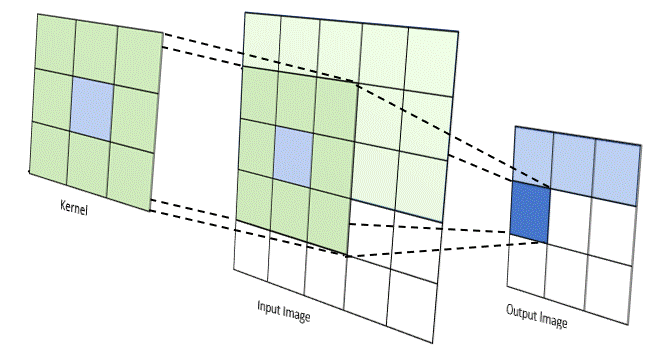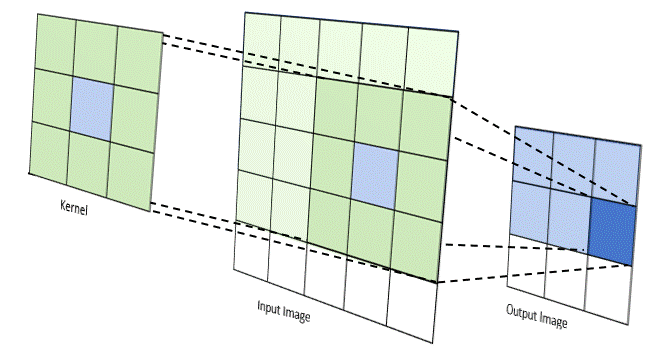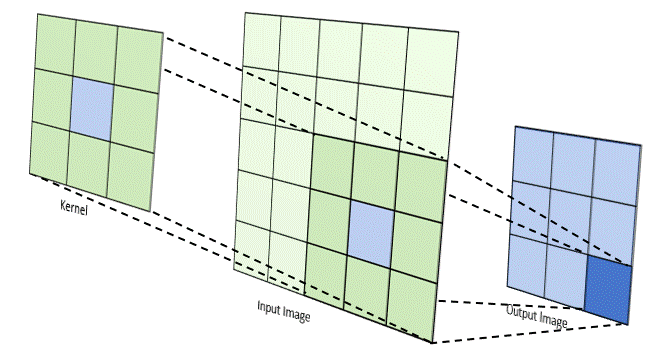
(Quá trình kernel trượt và tính tích chập)

2.2.2. Các Siêu tham số (Hyperparameters) Quyết định Kiến trúc

Việc thiết kế các lớp tích chập đòi hỏi sự hiểu biết sâu sắc về các siêu tham số, vì chúng ảnh hưởng trực tiếp đến kích thước đầu ra và khả năng học của mô hình. Bảng 1: Các siêu tham số chính trong lớp Tích chập

Siêu tham số	Ký hiệu	Mô tả	Tác động đến mô hình
Kernel Size	$K$ (hoặc $F$ )	Kích thước không gian của bộ lọc (thường lẻ: 3, 5, 7)	Kernel nhỏ giảm tham số, kernel lớn nhìn vùng rộng hơn nhưng tốn kém tính toán.⁸
Stride	$S$	Bước nhảy của bộ lọc khi trượt	$S=1$ : Giữ độ phân giải cao. $S=2$ : Giảm kích thước ảnh đi một nửa.¹¹
Padding	$P$	Số lượng viền 0 thêm vào xung quanh ảnh	Valid ( $P=0$ ): Ảnh nhỏ lại. Same padding: Giữ nguyên kích thước input/output.¹²
Dilation	$D$	Khoảng cách giữa các phần tử trong kernel	Tăng trường tiếp nhận mà không tăng tham số, hữu ích trong segmentation.¹³

Công thức tính kích thước đầu ra: Một trong những kỹ năng quan trọng nhất khi xây dựng CNN là tính toán kích thước tensor qua từng lớp. Giả sử đầu vào có kích thước $W_{in} \times H_{in}$ , bộ lọc $K$ , padding $P$ , stride $S$ , và dilation $D=1$ . Kích thước đầu ra $W_{out} \times H_{out}$ là 11:

$W_{out} = \left\lfloor \frac{W_{in} - K + 2P}{S} \right\rfloor + 1$

$H_{out} = \left\lfloor \frac{H_{in} - K + 2P}{S} \right\rfloor + 1$

Ví dụ: Với đầu vào MNIST $28 \times 28$ , dùng kernel $5 \times 5$ , padding $2$ , stride $1$ .

$W_{out} = \lfloor \frac{28 - 5 + 2(2)}{1} \rfloor + 1 = \lfloor 27 \rfloor + 1 = 28$

Đây là ví dụ của Same Padding, giúp giữ nguyên kích thước không gian.

2.3. Hàm Kích hoạt (Activation Functions): Phi tuyến hóa Mô hình

Sau phép tích chập (vốn là tổ hợp tuyến tính), ta cần đưa tín hiệu qua một hàm phi tuyến. Nếu không có hàm kích hoạt phi tuyến, một chuỗi các lớp tích chập xếp chồng lên nhau về mặt toán học sẽ chỉ tương đương với một lớp tích chập duy nhất, làm mất đi khả năng học các hàm phức tạp của mạng sâu.¹⁴

2.3.1. Sigmoid và Tanh: Hạn chế

Trong các thế hệ mạng nơ-ron đời đầu, hàm Sigmoid ( $\sigma(x) = \frac{1}{1+e^{-x}}$ ) và Tanh thường được sử dụng. Tuy nhiên, chúng gặp phải vấn đề nghiêm trọng gọi là Biến mất đạo hàm (Vanishing Gradient).

Khi đầu vào có giá trị tuyệt đối lớn (rất dương hoặc rất âm), đạo hàm của Sigmoid tiến về 0.
Trong quá trình lan truyền ngược (backpropagation), các gradient (vốn đã nhỏ) được nhân liên tiếp qua nhiều lớp (theo quy tắc chuỗi - chain rule). Nếu các đạo hàm cục bộ gần bằng 0, tín hiệu học tập sẽ bị triệt tiêu trước khi truyền về đến các lớp đầu tiên, khiến mạng không thể học được. ¹⁵

2.3.2. ReLU: Tiêu chuẩn Hiện đại

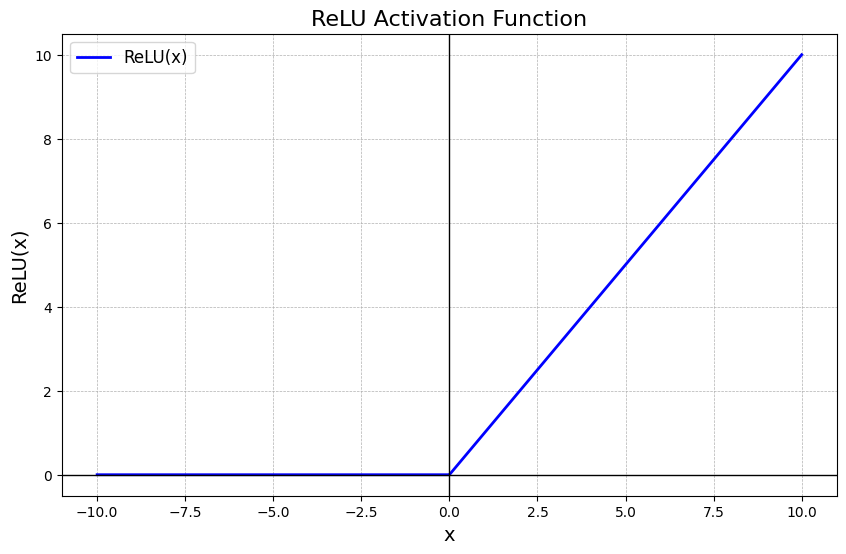
ReLU ( $f(x) = \max(0, x)$ ) đã trở thành lựa chọn mặc định cho CNN hiện đại.

Cơ chế: Giữ nguyên giá trị dương, gán 0 cho giá trị âm.
Ưu điểm: 1. Giải quyết Vanishing Gradient: Trong miền dương ( $x>0$ ), đạo hàm luôn bằng 1. Điều này cho phép gradient truyền nguyên vẹn qua nhiều lớp sâu. 2. Tính thưa (Sparsity): ReLU ép một phần các nơ-ron về 0 (trạng thái tắt). Sự kích hoạt thưa thớt này mô phỏng tốt hơn hoạt động sinh học và làm cho mô hình nhẹ hơn, giảm hiện tượng quá khớp. 3. Hiệu quả tính toán: Chỉ là phép so sánh ngưỡng, nhanh hơn nhiều so với hàm mũ trong Sigmoid/Tanh.
Biến thể: Leaky ReLU hoặc ELU đôi khi được dùng để khắc phục hiện tượng "Dying ReLU" (nơi nơ-ron bị chết vĩnh viễn ở miền âm).

2.4. Lớp Gộp (Pooling Layer)

Lớp Pooling thường được chèn vào giữa các lớp tích chập để giảm dần kích thước không gian (spatial dimensions) của bản đồ đặc trưng. Mục đích chính:

Giảm tham số và tính toán: Giảm kích thước ảnh đồng nghĩa với việc giảm số lượng phép tính ở các lớp sau (Nếu không có: Kích thước feature map quá lớn ở lớp sâu → tốn bộ nhớ, chậm).
Kiểm soát Overfitting: Loại bỏ các chi tiết thừa, buộc mạng tập trung vào các đặc trưng quan trọng nhất.
Bất biến dịch chuyển (Translation Invariance): Đây là tính chất quan trọng nhất. Max Pooling lấy giá trị lớn nhất trong một vùng (ví dụ $2 \times 2$ ). Nếu vật thể trong ảnh dịch chuyển nhẹ sang trái hoặc phải vài pixel, giá trị cực đại trong ô $2 \times 2$ đó vẫn có khả năng giữ nguyên. Điều này giúp CNN nhận diện vật thể bất kể vị trí chính xác của nó trong khung hình.

Các loại Pooling:

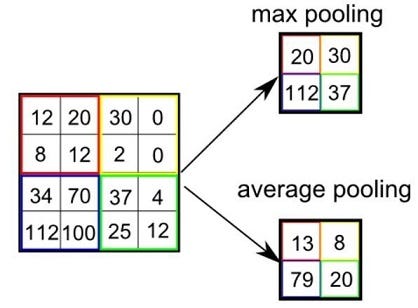
Max Pooling: Phổ biến nhất. Lấy giá trị lớn nhất. Hoạt động tốt trong việc giữ lại các đặc trưng nổi bật như cạnh, góc.23
Average Pooling: Lấy trung bình cộng. Thường làm mượt ảnh, ít được dùng ở các lớp giữa nhưng phổ biến ở lớp cuối cùng (Global Average Pooling) trong các kiến trúc hiện đại như ResNet để thay thế lớp Fully Connected.

Ví dụ: Ma trận 4×4 → sau max pooling 2×2 → ma trận 2×2.

2.5. Lớp Kết nối Đầy đủ (Fully Connected Layer)

Sau khi trích xuất đặc trưng qua chuỗi Conv-ReLU-Pool, dữ liệu đầu ra là một tensor 3 chiều (ví dụ: $7 \times 7 \times 64$ ). Để thực hiện phân loại, ta cần "duỗi phẳng" (flatten) tensor này thành một vector 1 chiều (kích thước $3136 \times 1$ ). Vector này được đưa vào mạng MLP truyền thống (Fully Connected Layers). Lớp cuối cùng thường sử dụng hàm Softmax để chuyển đổi các giá trị đầu ra (logits) thành phân phối xác suất cho $C$ lớp (với tổng xác suất bằng 1). Nhãn có xác suất cao nhất sẽ là dự đoán của mô hình.³

Mục đích: Sau khi feature map được flatten, các lớp FC kết hợp đặc trưng cấp cao để đưa ra quyết định phân loại (thường kết thúc bằng Softmax).

Công thức:

$\mathbf{z} = \mathbf{W} \mathbf{x} + \mathbf{b}, \quad \mathbf{y} = \text{Softmax}(\mathbf{z})_i = \frac{e^{z_i}}{\sum e^{z_j}}$

Lý do cần: Ánh xạ vector đặc trưng thành không gian lớp (class space). Nếu thiếu: Không có cơ chế đưa ra xác suất lớp cuối cùng → không phân loại được. Lưu ý hiện đại: Nhiều model mới (ResNet, Vision Transformer) thay FC bằng Global Average Pooling để giảm tham số.

3. Phần II: Thực hành - Áp dụng CNN cho Bài toán Phân loại Chữ số Viết tay (MNIST)

3.1. Giới thiệu Bộ dữ liệu MNIST

70.000 ảnh xám $28 \times 28$ chữ số viết tay (60.000 train, 10.000 test).
"Hello World" của Deep Learning, độ chính xác >99.7% với mô hình hiện đại.²⁴

3.2. Quy trình Xây dựng Bài giảng với PyTorch

3.2.1. Bước 1: Chuẩn bị Dữ liệu

import torch
import torchvision
import torchvision.transforms as transforms

# Pipeline xử lý ảnh
transform = transforms.Compose([
    transforms.ToTensor(),                              # Chuyển sang Tensor [0.0, 1.0]
    transforms.Normalize((0.1307,), (0.3081,))          # Chuẩn hóa về N(0,1)
])

# Tải dữ liệu
trainset = torchvision.datasets.MNIST(root='./data', train=True,
                                      download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64,
                                          shuffle=True, num_workers=2)

testset = torchvision.datasets.MNIST(root='./data', train=False,
                                     download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=1000,
                                         shuffle=False, num_workers=2)

3.2.2. Bước 2: Kiến trúc CNN (LeNet-5 Hiện đại hóa)

import torch.nn as nn
import torch.nn.functional as F

class MNIST_CNN(nn.Module):
    def __init__(self):
        super(MNIST_CNN, self).__init__()
        self.conv1 = nn.Conv2d(1, 32, kernel_size=3, padding=1)
        self.conv2 = nn.Conv2d(32, 64, kernel_size=3, padding=1)
        self.fc1 = nn.Linear(64 * 7 * 7, 128)
        self.fc2 = nn.Linear(128, 10)

    def forward(self, x):
        x = F.relu(self.conv1(x))          # (32, 28, 28)
        x = F.max_pool2d(x, 2)             # (32, 14, 14)
        x = F.relu(self.conv2(x))          # (64, 14, 14)
        x = F.max_pool2d(x, 2)             # (64, 7, 7)
        x = torch.flatten(x, 1)            # (3136)
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return x

3.2.3. Bước 3: Huấn luyện

import torch.optim as optim

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = MNIST_CNN().to(device)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

epochs = 5
for epoch in range(epochs):
    running_loss = 0.0
    for data in trainloader:
        inputs, labels = data
        inputs, labels = inputs.to(device), labels.to(device)

        optimizer.zero_grad()
        outputs = model(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
    print(f'Epoch {epoch+1}, Loss: {running_loss / len(trainloader):.3f}')

Kết quả kỳ vọng: ~98.5–99.2% accuracy trên test set.

4. Phần III: Thách thức Nâng cao - Phân loại Thời trang (Fashion-MNIST)

4.1. Fashion-MNIST

Giữ nguyên kích thước như MNIST nhưng khó hơn nhiều (accuracy với kiến trúc đơn giản ~89–91%). Các lớp: T-shirt/top, Trouser, Pullover, Dress, Coat, Sandal, Shirt, Sneaker, Bag, Ankle boot.

4.2. Phân tích Ma trận Nhầm lẫn

Các cặp dễ nhầm:

Shirt vs. T-shirt/top vs. Coat vs. Pullover
Sneaker vs. Ankle boot vs. Sandal

4.3. Chiến lược Tối ưu hóa (>93% Accuracy)

Batch Normalization: Conv → BN → ReLU
Dropout
Data Augmentation: RandomHorizontalFlip, RandomRotation(±10°)

4.4. Kiến trúc Đề xuất: Advanced VGG-Style CNN

class AdvancedFashionCNN(nn.Module):
    def __init__(self):
        super(AdvancedFashionCNN, self).__init__()
        self.layer1 = nn.Sequential(
            nn.Conv2d(1, 32, kernel_size=3, padding=1),
            nn.BatchNorm2d(32),
            nn.ReLU(),
            nn.Conv2d(32, 64, kernel_size=3, padding=1),
            nn.BatchNorm2d(64),
            nn.ReLU(),
            nn.MaxPool2d(2)                # 14x14x64
        )
        self.layer2 = nn.Sequential(
            nn.Conv2d(64, 128, kernel_size=3, padding=1),
            nn.BatchNorm2d(128),
            nn.ReLU(),
            nn.Conv2d(128, 128, kernel_size=3, padding=1),
            nn.BatchNorm2d(128),
            nn.ReLU(),
            nn.MaxPool2d(2)                # 7x7x128
        )
        self.fc1 = nn.Linear(7*7*128, 512)
        self.drop = nn.Dropout(0.5)
        self.fc2 = nn.Linear(512, 128)
        self.fc3 = nn.Linear(128, 10)

    def forward(self, x):
        x = self.layer1(x)
        x = self.layer2(x)
        x = x.view(x.size(0), -1)
        x = F.relu(self.fc1(x))
        x = self.drop(x)
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

5. Phần IV: Kết nối Giáo dục và Tài liệu Tham khảo

5.1. Bối cảnh Đào tạo AI tại Việt Nam

HUST: Tích hợp Deep Learning sâu, lab yêu cầu phân tích siêu tham số.
VNU-HCM: Fashion-MNIST làm assignment, thi đấu trên Kaggle.
VinUni, Fulbright: Áp dụng giáo trình CS231n, chú trọng Explainable AI.

5.2. Tài liệu Tham khảo

CS231n Convolutional Networks
Convolutional Neural Networks (CNNs): An Illustrated Explanation - XRDS
[Deep Learning] Tìm hiểu về mạng tích chập (CNN)

6. Kết luận

Mạng Nơ-ron Tích chập (CNN) đại diện cho một bước nhảy vọt trong khả năng mô phỏng thị giác sinh học của máy tính. Từ những khái niệm toán học cơ bản về tích chập và gộp, đến các kiến trúc phức tạp giải quyết bài toán Fashion-MNIST, CNN đã chứng minh tính hiệu quả vượt trội. Báo cáo này đã cung cấp một lộ trình toàn diện: đi từ việc hiểu "tại sao" (lý thuyết) đến biết "làm thế nào" (thực hành code), và cuối cùng là "làm thế nào cho tốt hơn" (tối ưu hóa nâng cao). Đây là nền tảng thiết yếu cho bất kỳ kỹ sư hay nhà nghiên cứu nào muốn dấn thân vào lĩnh vực AI và Thị giác máy tính đầy tiềm năng.

Mở rộng: Dense là tên gọi kỹ thuật của Lớp kết nối đầy đủ (Fully Connected Layer)

Đây là lớp mạng nơ-ron truyền thống nhất (giống như trong các mạng MLP cũ). Dưới đây là giải thích chi tiết về bản chất, vai trò và lý do tại sao nó được gọi là "Dense".

1. Tại sao gọi là "Dense" (Dày đặc)?

Tên gọi này xuất phát từ cách các nơ-ron kết nối với nhau:

Kết nối toàn bộ: Trong một lớp Dense, mỗi nơ-ron ở lớp này được kết nối với tất cả các nơ-ron của lớp trước đó.
Mạng lưới dày đặc: Nếu bạn vẽ các đường kết nối ra giấy, bạn sẽ thấy một mạng lưới chằng chịt, dày đặc các đường thẳng nối giữa các điểm. Không có nơ-ron nào bị bỏ sót.

2. Vai trò của lớp Dense trong CNN

Trong bài toán MNIST (và hầu hết các bài toán CNN), lớp Dense đóng vai trò là "Bộ não ra quyết định" sau khi đôi mắt (các lớp Conv2D) đã quan sát xong.

Hãy tưởng tượng quy trình như sau:

Lớp Conv2D & Pooling (Trích xuất đặc trưng): Đóng vai trò như "mắt". Chúng quét ảnh và phát hiện ra các đặc điểm: "Chỗ này có nét cong", "Chỗ kia có nét thẳng", "Góc này có một vòng tròn".

Kết quả: Một tập hợp các bản đồ đặc trưng (feature maps) dưới dạng hình khối 3D.

Lớp Flatten: Duỗi phẳng hình khối 3D đó thành một danh sách dài (vector 1D). Ví dụ: "Có 1 nét cong ở trên, 1 nét thẳng ở dưới...".
Lớp Dense (Phân loại): Đóng vai trò như "bộ não". Nó nhìn vào danh sách đặc điểm đó và tổng hợp lại để đưa ra kết luận:

Tư duy: "Nếu có một vòng tròn ở trên (đặc trưng A) VÀ một nét móc ở dưới (đặc trưng B), thì khả năng cao đây là số 9".
Nó thực hiện việc này bằng cách gán trọng số (weights) cho từng đặc điểm.

3. Công thức Toán học

Về mặt toán học, lớp Dense thực hiện phép biến đổi tuyến tính đơn giản:

: Vector đầu vào (dữ liệu từ lớp trước).
: Ma trận trọng số (Weights) - đây là cái mạng sẽ "học".
: Vector hệ số chệch (Bias).
: Hàm kích hoạt (như ReLU hoặc Softmax).

4. So sánh Dense và Conv2D

Để hiểu rõ hơn, hãy xem sự khác biệt giữa hai loại lớp quan trọng nhất này:

Đặc điểm	Conv2D (Tích chập)	Dense (Kết nối đầy đủ)
Cách kết nối	Cục bộ (Local): Một nơ-ron chỉ nhìn vào một vùng nhỏ của ảnh (ví dụ 3x3 pixel).	Toàn cục (Global): Một nơ-ron nhìn vào toàn bộ dữ liệu đầu vào cùng lúc.
Số lượng tham số	Ít: Do chia sẻ trọng số (cùng 1 bộ lọc quét khắp ảnh).	Rất nhiều: Do mỗi kết nối có một trọng số riêng biệt.
Mục đích	Tìm kiếm các đặc trưng hình ảnh (cạnh, góc, hình dạng).	Tổng hợp đặc trưng để ra quyết định (đây là cái gì?).
Vị trí	Thường ở phần đầu của mạng.	Thường ở phần cuối của mạng.

5. Trong đoạn code MNIST

Hãy nhìn lại đoạn code chúng ta vừa viết:

# Duỗi phẳng dữ liệu thành vector
model.add(layers.Flatten())

# Lớp Dense 1 (Lớp ẩn):
# Học cách kết hợp các đặc trưng phi tuyến.
model.add(layers.Dense(64, activation='relu'))

# Lớp Dense 2 (Lớp đầu ra):
# Đưa ra xác suất cho 10 số (0-9).
model.add(layers.Dense(10, activation='softmax'))

layers.Dense(64, ...): Tạo ra một lớp có 64 nơ-ron. Mỗi nơ-ron này kết nối với tất cả các phần tử trong vector đầu vào từ lớp Flatten.
layers.Dense(10, ...): Đây là lớp cuối cùng, mỗi nơ-ron đại diện cho một con số (0, 1, ..., 9). Giá trị của nơ-ron nào cao nhất thì đó là dự đoán của máy.