[Machine Learning] Tổng quan về mạng Neural nhân tạo

Vấn đề

Trong các mô hình tuyến tính, chúng ta có thể sử dụng dễ dàng các phương pháp như hồi quy tuyến tính, hồi quy logictics, phân tích thành phần chính, ... để chọn ra hàm số xấp xỉ tốt với mô hình. Tuy nhiên vấn đề bộc phát ở các mô hình phi tuyến tính, nếu muốn sử dụng lại các phương pháp trên, dạng hàm số đặt ra là hoàn toàn dựa vào ý kiến chủ quan của người làm. Ở các dạng bài này, hồi quy tuyến tính thể hiện rõ sự điểm yếu ở các bài toán với lượng dữ liệu lớn hoặc không thể biểu diễn trên mặt phẳng hay không gian. Phương pháp Support Vector Machine đơn thuần là phân chia các miền dữ liệu chứ không có một phép toán xác suất ở trong tính toán. Mạng Neural nhân tạo ra đời giải quyết các vấn đề đó. Nó là tập hợp của rất nhiều kiến thức của giải tích hàm, và backpropagation giúp cho kỹ thuật này trở thành hiện thực.

Mô hình mạng Neural nhân tạo

Mô hình đã được biểu diễn trực quan của mạng Neural nhân tạo đầy rẫy trên mạng, tôi lấy đại tấm đầu tiên tìm được trên Google Hình ảnh.

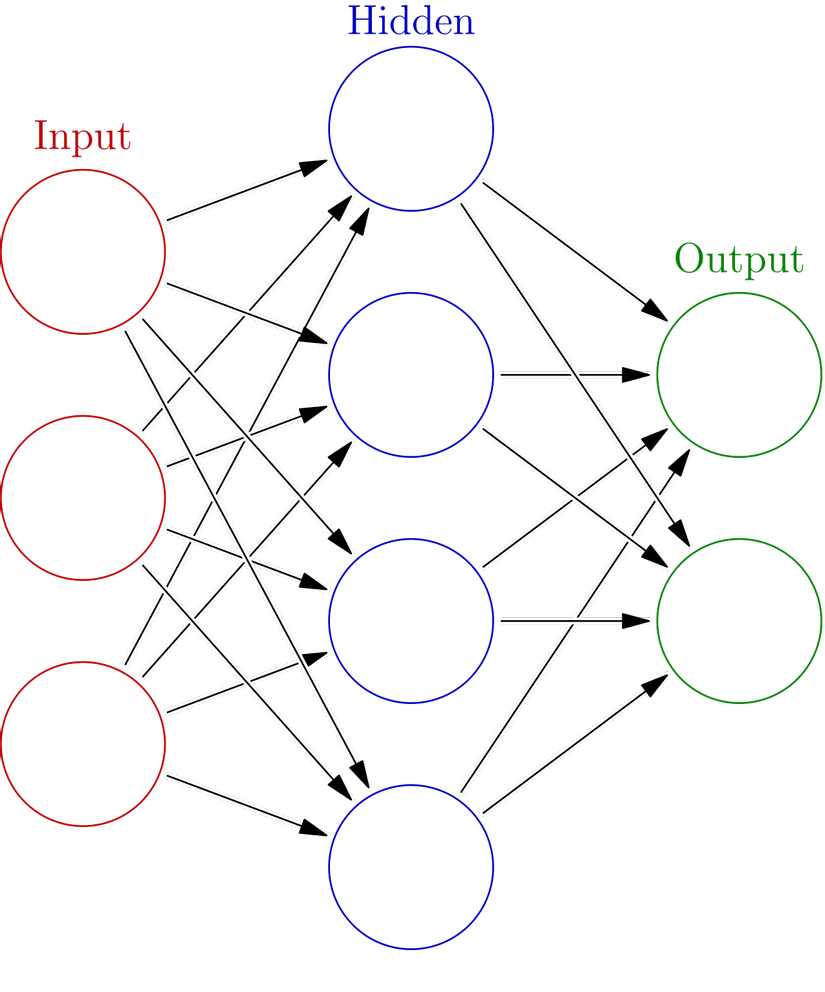
Nhìn nó khá giống đồ thị nhưng không phải là đồ thị trong cấu trúc rời rạc. Ý tưởng là mỗi ở lớp sau là tổ hợp tuyến tính của các nút lớp phía trước, sau đó được ánh xạ bởi một hàm $\sigma$ nào đó, các hệ số của tổ hợp tuyến tính được ghi ở trên các mũi tên. Với việc biểu diễn trực quan thế này thì ta có một nhận xét đó là nếu một mũi tên nào đó được ghi số 0 thì coi như ta có thể bỏ đi mũi tên đó luôn. Vậy nên khi tìm một mạng Neural biểu diễn hàm số $f: \mathbb{R}^n \to \mathbb{R}^m$, ta chỉ cần tìm các hàm $f_i: \mathbb{R}^n\to\mathbb{R}$ và sau đó gộp chúng lại với nhau thành một mạng Neural bằng các mũi tên ghi số $0$. Tóm lại bài toán ta cần giải quyết sẽ thu gọn còn: Với hàm $g: \mathbb{R}^n\to\mathbb{R}$ cho trước, tìm hàm $f: \mathbb{R}^n\to\mathbb{R}$ xấp xỉ $g$ có dạng:

$$f(x) = \sum\limits_{i = 1}^{N} v_i\sigma\left(w_ix +b_i\right)$$

Universal approximation theorem

Với một hàm $\sigma:\mathbb{R}\to\mathbb{R}$ liên tục, miền giá trị hữu hạn, khác hằng. Gọi $B$ là tập conpact con của $\mathbb{R}^n$. Khi đó các hàm có dạng:

$$F(x) = \sum\limits_{i = 1}^{N}v_i\sigma(w_i^Tx+b_i)$$

hầu khắp $C(B)$. Nghĩa là ta luôn tìm ra một xấp xỉ của $f \in C(B)$ có dạng như trên nếu $\sigma$ thỏa mãn cả ba điều kiện trên.

Như vậy các hàm $\sigma$ như $\dfrac{1}{1+e^{-x}}, \tanh(x), \arctan(x)$ được sử dụng làm activation cho mạng Neural. Đối với hàm $\text{max}(x, 0)$, dù nó có miền giá trị là $\mathbb{R}^{\geqslant}$ và không phải miền hữu hạn nhưng nó vẫn có thể dùng trong mạng Neural vì ở một bước nhân $w_i^Tx$ là một dạng của ánh xạ tuyến tính. Do đó ta cũng có thể tạo ra một tổ hợp tuyến tính có dạng:

$$\text{max}(x, 0) - \text{max}(x - 1, 0) = \begin{cases}0, & \text{if }x < 0 \\ x, & \text{if }x \in [0, 1] \\ 1,& \text{if }x > 1 \end{cases}$$

Và hiển nhiên hàm này liên tục, miền giá trị thuộc tập đóng $[0, 1]$ và khác hằng.

Chú ý là ta chỉ có thể xấp xỉ một hàm trên một compact, chứ không thể xấp xỉ trên toàn miền không gian. Ví dụ có thể xấp xỉ $f(x) = x^2$ trên $[-10,10]$ chứ không thể trên cả $\mathbb{R}$ được.

Gradient Descent

Gradient Descent là một kỹ thuật giúp tìm được cực tiểu cho một hàm số với ý tưởng là đi ngược lại với hướng vector Gradient của hàm số đó. Đây là một kỹ thuật rất phổ biến ở thời điểm hiện tại. Tôi còn nhìn thấy nó trong mấy bài hồi quy tuyến tính ở nhiều khóa học vì nó đơn giản hơn việc giải tay cực trị nhiều và độ phủ sóng của nó là mọi hàm số có đạo hàm khác 0:

$$\begin{cases}x_0\\x_n = x_{n-1} - \eta\nabla f(x_{n-1})\end{cases}$$

Có một số phiên bản như Momentum, Stochastic, ... nhưng ý tưởng cơ bản vẫn ở công thức truy hồi trên.

Backpropagation

Với mớ lý thuyết ở trên thì ta có thể chắc chắn rằng tồn tại một mạng Neural xấp xỉ một hàm cho trước trong một tập Compact. Vậy làm thế nào để có thể tìm ra được mô hình mạng Neural đó. Ta sẽ thiết kế mạng Neural theo mô hình phép toán các ma trận:

Gọi $W_i$ là ma trận trọng số của lớp thứ $i$, $b_i$ là vector bias của lớp thứ $i$, $a_i$ là đầu ra của lớp thứ $i$ và $\sigma$ là hàm kích hoạt, khi đó ta định nghĩa với đầu vào là $X$:

$$\begin{cases}a_0 = X \\ X_i = W_ia_{i-1}+b_{i} \\ a_{i} = \sigma\left(X_i\right) \\ a_n = X_n \end{cases}$$

Giả sử đầu ra tương ứng là $y$ thì ta cần $||a_n - y||^2$ càng bé để thể hiện mạng Neural có xấp xỉ càng tốt.

Với công thức truy hồi như trên, việc tính các đại lượng gradient của $||X_n - y||^2$ theo $W_i$ và $b_i$ được tính dựa vào lớp sau nó (lớp sau được tính trước). Do đó kỹ thuật Gradient Descent tỏ ra hiệu quả trong việc điều chỉnh dần dần các đại lượng $W_i, b_i$ để tìm ra được mô hình mạng Neural thích hợp.

Hàm số được dùng để làm activation hiện tại phổ biến là $\text{max}(x, 0)$ vì nó phủ sóng trên $\mathbb{R}^{\geqslant}$ chứ không gò bó vào khoảng nhỏ $[0, 1]$ nên việc tính các đại lượng thường ở mức không xấp xỉ $0$, và do đó tốc độ hội tụ khi dùng Gradient Descent cũng sẽ cao hơn so với các hàm số khác.

Không chỉ dừng lại ở bài toán hồi quy, mạng Neural có thể giải quyết các bài toán phân lớp với một hàm lỗi là croos-entropy với kích hoạt ở lớp đầu ra là sort-max, và đặc biệt công thức đạo hàm của cross-entropy lại giống với $||X_n-y||^2$

Tài liệu tham khảo:

Universal approximations of invariant maps by neural networks