Machine Learning - Linear Regression with One Variable
Bài đăng này đã không được cập nhật trong 4 năm
Chào các bạn, cũng đã gần 1 tháng từ khi tôi viết bài đầu tiên về machine learning - tổng quan về machine learning Với kì vọng mỗi tuần 1 bài viết, vừa là để tổng kết những gì đã học được, vừa là để làm tài liệu mình lưu trữ sau này. Nhưng kế hoạch đã đổ bể ngay tuần đầu tiên bởi không chỉ có quá nhiều thứ để học, hiểu và viết thành 1 bài hoàn chỉnh mà còn bởi đồ án và công việc học tập tại trường xâm chiếm gần như toàn bộ thời gian. Đến hôm nay mới có thời gian quay lại và viết 1 bài để chia sẻ kiến thức và kinh nghiệm với mọi người.
Linear Regression with one variable
Chủ đề của bài viết này sẽ là Linear Regresssion with one variable (tạm dịch: Hồi quy tuyến tính một biến) là một trong những giải thuật đơn giản và dễ triển khai nhất trong machine learning. Thực chất khái niệm này đã có đề cập tới ngay từ bài viết trước trong series về ML của tôi, nếu bạn còn nhớ thì tôi đã nêu một ví dụ về việc dự đoán giá nhà dựa trên diện tích, đó cũng là 1 bài toán mà ta có thể áp dụng linear regression để giải quyết.
Model Representation
Trước hết, hãy cùng tìm hiểu một mô hình chung cho quá trình apply Linear Regression vào để giải quyết bài toán cụ thể.
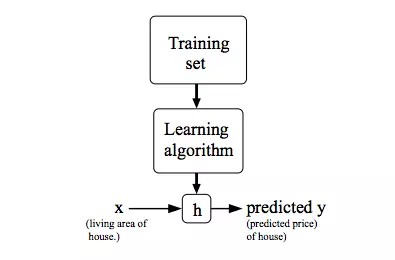 Giống như rất nhiều cấu trúc phần mềm hoạt động, một cấu trúc chung cho việc sử dụng ML để giải quyết các bài toán, cũng bao gồm 3 phần chính.
Giống như rất nhiều cấu trúc phần mềm hoạt động, một cấu trúc chung cho việc sử dụng ML để giải quyết các bài toán, cũng bao gồm 3 phần chính.
- Phần 1: input, hay x. Đầu vào ở đây chính là dữ liệu, thông tin mà ta đã có, và đang cần tìm đầu ra. Vẫn với ví dụ dữ đoán giá nhà cửa dựa trên diện tích. Ta có một tập các dữ liệu gồm diện tích nhà và giá tương ứng. Giờ tôi có 1 ngôi nhà có diện tích là 1000m2, cần tìm giá của nó là bao nhiêu. Thì 1000m2 đây chính là input của chương trình.
- Phần 2: output, hay y. output là giá của ngôi nhà 1000m2 ở trên, cũng chính là kết quả mà ta mong muốn từ đầu vào.
- Phần 3: process (xử lý). Quá trình xử lý ở đây sẽ diễn ra như sau: ta có một tập dữ liệu có sẵn (Training set), dựa trên tập dữ liệu này, mối quan hệ giữa đầu vào, đầu ra, ... ta sẽ tìm ra được một hàm quan hệ giữa x và y gọi là Hypothesis Function (kí hiệu là h). Thông qua hàm h biểu diễn mối quan hệ giữa x và y, ta sẽ tìm được y nếu biết x. Ví dụ với y = ax + b chẳng hạn, thì ax + b chính là Hypothesis Function, sau một vài quá trình xử lý ta tìm được h = 3x + 1, vậy nếu x = 1000m2, thì ta chỉ việc thay vào hàm h là tìm được giá trị y tương ứng = 3001
Hypothesis Function
Với Linear Regresssion with one variable thì hypothesis function sẽ có dạng chung là:
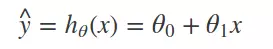 Nếu biễu diễn trên biểu đồ thì đây sẽ là 1 đường thẳng, và gần như chắc chắn là nó sẽ chỉ tiệm cận chứ không đi qua hầu hết các điểm dữ liệu của tập training set.
Mục tiêu của giải thuật Linear Regression chính là đi tìm các tham số θ (đọc là theta), từ đó hình thành nên hàm h, một khi đã biểu diễn được mối quan hệ giữa x và y thì ta sẽ thu được output cần thiết từ đầu vào x. Và đương nhiên, các tham số θ tìm được đều chỉ là tương đối, tức là đạt độ chính xác lớn nhất có thể, để map input data với output data.
Nếu biễu diễn trên biểu đồ thì đây sẽ là 1 đường thẳng, và gần như chắc chắn là nó sẽ chỉ tiệm cận chứ không đi qua hầu hết các điểm dữ liệu của tập training set.
Mục tiêu của giải thuật Linear Regression chính là đi tìm các tham số θ (đọc là theta), từ đó hình thành nên hàm h, một khi đã biểu diễn được mối quan hệ giữa x và y thì ta sẽ thu được output cần thiết từ đầu vào x. Và đương nhiên, các tham số θ tìm được đều chỉ là tương đối, tức là đạt độ chính xác lớn nhất có thể, để map input data với output data.
Ví dụ: ta có bảng training set sau
 Chưa vội đề cập đến việc áp dụng Linear Regression, nhìn vào dữ liệu ta có thể đưa ra dữ đoán là θ0 = 2 và θ1 = 2, Hypothesis function: hθ(x)=2+2x
Với x = 4, ta sẽ predict là y = 10. Đây là 1 ví dụ khá đơn giản mà ta có thể đoán luôn hàm h, nhưng với các dữ liệu phức tạp hơn, đòi hỏi độ chính xác cao hơn thì sẽ phải có các phương pháp tốt và tối ưu hơn. Hãy cùng đi vào 2 khái niệm Cost Function (hàm mất mát) và Gradient Descent (giải thuật độ dốc).
Chưa vội đề cập đến việc áp dụng Linear Regression, nhìn vào dữ liệu ta có thể đưa ra dữ đoán là θ0 = 2 và θ1 = 2, Hypothesis function: hθ(x)=2+2x
Với x = 4, ta sẽ predict là y = 10. Đây là 1 ví dụ khá đơn giản mà ta có thể đoán luôn hàm h, nhưng với các dữ liệu phức tạp hơn, đòi hỏi độ chính xác cao hơn thì sẽ phải có các phương pháp tốt và tối ưu hơn. Hãy cùng đi vào 2 khái niệm Cost Function (hàm mất mát) và Gradient Descent (giải thuật độ dốc).
Cost Function
Mục tiêu của cost function là để tính độ chính xác của thuật toán ta áp dụng, bằng cách lấy trung bình sai số giữa các kết quả dự đoán và kết quả thực. Công thứ của cost function như sau:
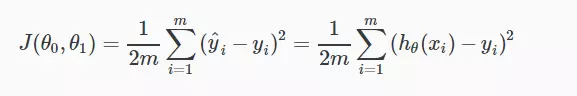 Ở đây ta kí hiệu hàm mất mát là J(θ), sở dĩ đây là hàm của theta bởi như mình đã lý giải ở trên, mục tiêu là phải tìm được các tham số θ thích hợp trong h, nên cost function sẽ phải là hàm của θ.
m là kích cỡ của training set, hθ(xi) chính là đầu ra sau khi dự đoán với giải thuật linear regression đối với training set thứ i, yi là kết quả thực sự của training set thứ i
Hàm này tính độ chính xác của hypothesis function, tức là độ lệch của đầu ra từ giải thuật so với kết quả thực tế của training set. Nhưng như vậy thì công thức trên có vẻ thơi thừa. Đáng nghẽ nó chỉ phải là:
Ở đây ta kí hiệu hàm mất mát là J(θ), sở dĩ đây là hàm của theta bởi như mình đã lý giải ở trên, mục tiêu là phải tìm được các tham số θ thích hợp trong h, nên cost function sẽ phải là hàm của θ.
m là kích cỡ của training set, hθ(xi) chính là đầu ra sau khi dự đoán với giải thuật linear regression đối với training set thứ i, yi là kết quả thực sự của training set thứ i
Hàm này tính độ chính xác của hypothesis function, tức là độ lệch của đầu ra từ giải thuật so với kết quả thực tế của training set. Nhưng như vậy thì công thức trên có vẻ thơi thừa. Đáng nghẽ nó chỉ phải là:
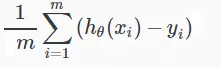 Lý do ta lấy bình phương và 1/2 đơn giản để cho dễ tính. Bình phương lên để tránh trường hợp số âm (cũng chính vì thế mà hàm này còn được gọi là Squared error function, còn chia cho 2 sẽ thuận tiện hơn cho việc tính đạo hàm, còn sao phải tính đạo hàm sẽ có ở phần tiếp theo gradient descent
Vậy là bạn đã hiểu phần nào công thức của hàm mất mát, chúng ta sẽ bằng một cách nào đó, làm cho hàm mất mát là nhỏ nhất, hàm này càng nhỏ, tức là sai số đự đoán càng nhỏ, nói cách khác, giải thuật càng chính xác (đa phần là thế).
Nếu các bạn còn nhớ đồ thị biểu diễn hypothesis function:
Lý do ta lấy bình phương và 1/2 đơn giản để cho dễ tính. Bình phương lên để tránh trường hợp số âm (cũng chính vì thế mà hàm này còn được gọi là Squared error function, còn chia cho 2 sẽ thuận tiện hơn cho việc tính đạo hàm, còn sao phải tính đạo hàm sẽ có ở phần tiếp theo gradient descent
Vậy là bạn đã hiểu phần nào công thức của hàm mất mát, chúng ta sẽ bằng một cách nào đó, làm cho hàm mất mát là nhỏ nhất, hàm này càng nhỏ, tức là sai số đự đoán càng nhỏ, nói cách khác, giải thuật càng chính xác (đa phần là thế).
Nếu các bạn còn nhớ đồ thị biểu diễn hypothesis function:
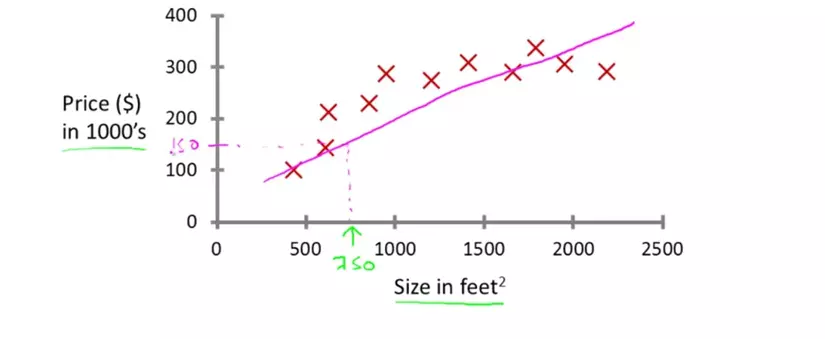 ở đây, cost function cũng chính là trung bình khoảng cách giữa các điểm giá trị thật với đồ thị thẳng biểu diễn hypothesis function, đồ thị này càng đi qua và gần nhiều điểm, khoảng cách giữa các điểm này với đường thẳng biểu diễn hypothesis function sẽ càng nhỏ, hàm dự đoán của chúng ta càng chính xác.
ở đây, cost function cũng chính là trung bình khoảng cách giữa các điểm giá trị thật với đồ thị thẳng biểu diễn hypothesis function, đồ thị này càng đi qua và gần nhiều điểm, khoảng cách giữa các điểm này với đường thẳng biểu diễn hypothesis function sẽ càng nhỏ, hàm dự đoán của chúng ta càng chính xác.
Gradient Descent
Tới phần này, ta đã xác định được một đường đi cụ thể: muốn dự đoán được giá -> xác định hypothesis function -> minimize cost function. Và nếu ai học tốt toán một chút thì chỗ này sẽ nhận ra, muốn đi giải một bài toán tối ưu, một trong các phương pháp hay dùng nhất, chính là giải phương trình đạo hàm bằng 0. Hàm cost function là một hàm bậc hai, có đồ thị hình chum, điểm thấp nhất (có giá trị nhỏ nhất) cũng chính là điểm có đạo hàm bằng 0. Và đó cũng chính là công việc của giải thuật gradient descent.
Giải thuật gradient descent cũng không có gì phức tạp, ta sẽ lặp lại việc tính θ cho đến khi nó bất biến (lúc này đạo hàm sấp xỉ 0)
Thực hiện tính toán θ cho đến khi hội tụ:
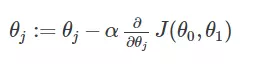 Với hàm hypothesis function ở trên:
Với hàm hypothesis function ở trên:
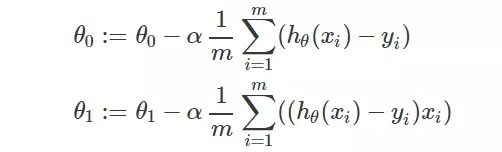 Kết quả này thu được sau khi tính đạo hàm của hypothesis function ở trên. Với mỗi bước này, 2 tham số theta được thay đổi, và sẽ lặp lại việc thay đổi này cho tới khi theta bất biến hoặc thay đổi quá nhỏ (coi không đáng kể).
Kết quả này thu được sau khi tính đạo hàm của hypothesis function ở trên. Với mỗi bước này, 2 tham số theta được thay đổi, và sẽ lặp lại việc thay đổi này cho tới khi theta bất biến hoặc thay đổi quá nhỏ (coi không đáng kể).
Conclusion
Ở trên là một dãy các lý thuyết và khái niệm cần nhớ, bài tiếp theo về machine learning cũng sẽ vẫn thế =)) nhưng mình sẽ cố gắng đưa thêm cả code implement giải thuật vào nữa. Cũng định đưa luôn từ bài này, nhưng thực sự khi tính toán sẽ áp dụng hơi khác so với lý thuyết một chút, điển hình là ta sẽ dùng các ma trận để tính toán, chứ không phải giải và tính toán từng giá trị như trên. Ngay bài sau thôi mình sẽ đề cập tới một vài khái niệm căn bản về đại số, đồng thời sẽ có code (python) implement Linear Regression with one variable để các bạn hình dung tốt hơn các bước thực hiện. Cám ơn đã đọc tới tận dòng này của bài viết. Hẹn gặp lại.
Bài viết tham khảo từ khóa học Machine Learning của giáo sư Andrew Ng, đại học Stanford
All rights reserved