Giới thiệu

Trong bài viết này mình sẽ tóm tắt các ý tưởng chính của phương pháp DPO trong bài báo DPO Paper. Về cơ bản, đây là kỹ thuật để align hiệu quả các model LLM. Một số model 7B sử dụng phương pháp này có thể đạt performance tương đương với các model 70B, thậm chí là hơn . Ví dụ như Mixtral 8x7B sử dụng DPO đạt đến performance của LLaMa 70B. Okay! Vậy thì đi thử sâu hơn vào phương pháp này xem nó có gì nhé

Nhắc lại PPO

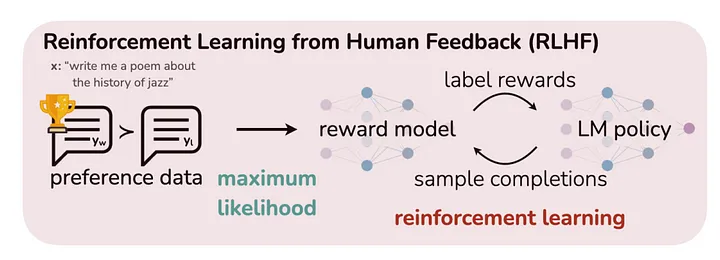
Trước khi có DPO, trong mô hình RLHF truyền thống, ta phải finetune 2 model riêng biệt: Reward model và Policy model. Quy trình sẽ là:

• Train 1 reward model từ human preference. Human preference ở đây các bạn có thể hiểu là nhãn feedback của con người. Ví dụ như thích phản hồi nào hơn, hoặc gán điểm cho phản hồi.
• Sau đó, reward model này sẽ được đóng băng (frozen) và được sử dụng để train LLM (Policy model) sử dụng thuật toán RL, ví dụ như PPO.

Để tối ưu chi phí (chi phí tạo nhãn bởi con người), ta sử dụng reward model để "xấp xỉ" feedback của con người, chính vì vậy phương pháp này có tên là Proximal Policy Optimization (PPO). Nói chung là, chất lượng của model LLM sẽ phụ thuộc rất nhiều vào Reward model, hay nói 1 cách khác thành bại tại Reward model

Để có một reward model lý tưởng, ta sẽ có một giả định rằng sở thích (preferences) của con người là ở dưới dạng xác suất. Vì vậy, chúng ta có thể biểu diễn trong một mô hình Bradley-Terry như sau:

$$p^*(y_1 \succ y_2 \mid x) = \frac{\exp \left( r^*(x, y_1) \right)}{\exp \left( r^*(x, y_1) \right) + \exp \left( r^*(x, y_2) \right)}.$$

Okay! thử soi qua từng biến trong phương trình xem ta có gì $p^*$ có nghĩa là phân phối xác suất tối ưu (optimal probability distribution), hay phân phối mà mô hình nên coi là ground truth. $y_1$ và $y_2$ là hai phản hồi từ mô hình mà chúng ta sẽ so sánh. $x$ là prompt được dùng cho LLM. $r^*$ có nghĩa là optimal reward function. Để train mô hình optimal probability distribution, bạn cần đưa cho mô hình này các reward từ optimal reward function.

Tuy nhiên, việc biết chính xác 100% probability distribution của human preference là rất khó, nếu không muốn nói là không thể. Vì lý do này, chúng ta quay lại tập trung vào reward model. Bài toán bây giờ sẽ là tìm cách xác định $r^*$.

Bây giờ ta cần xây dựng 1 hàm loss function cho việc training reward model. Reward model sẽ được train trên Human preference data, data này sẽ đại diện 1 phần trong probability distribution của human preference. Khi này, loss function sẽ như sau:

$$\mathcal{L}_R(r_\phi, \mathcal{D}) = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}} [\log \sigma (r_\phi(x, y_w) - r_\phi(x, y_l)))]$$

Ở đây, $r_\phi$ là reward model đang được training, $\mathcal{D}$ là tập human preference data, $y_w$ là phản hồi được ưa thích và $y_l$ là phản hồi không được ưa thích. Để cho dễ hiểu, tác giả coi đây là bài toán binary-classification.

Sau khi tối ưu xong reward model, ta sẽ sử dụng model này để finetune model LLM dựa trên sự khác biệt giữa policy cũ ($\pi_{\text{ref}}$) và policy mới ($\pi_\theta$). Một điều đáng chú ý là nhóm tác giả sử dụng KL divergence để ngăn mô hình bị biến đổi quá nhiều. Lý do cho việc này là để đảm bảo mô hình vẫn giữ được những feature trong quá trình pretraining và SFT trước đó.

$$\max_{\pi_\theta} \mathbb{E}_{x \sim \mathcal{D}, y \sim \pi_\theta(y|x)}[r_\phi(x, y)] - \beta D_{KL}[\pi_\theta(y|x) \| \pi_{\text{ref}}(y|x)]$$

Mặc dù phương pháp PPO hiệu quả, nhưng nó có một nhược điểm lớn đó là phải train một mô hình hoàn toàn tách biệt (chính là reward model), dẫn đến tốn kém chi phí và yêu cầu lượng lớn dữ liệu bổ sung.

DPO cải thiện PPO như nào?

Với phương pháp DPO, ta sẽ không sử dụng Reward model cho quá trình align model LLM, từ đó giảm được chi phí tạo dữ liệu và tài nguyên sử dụng.

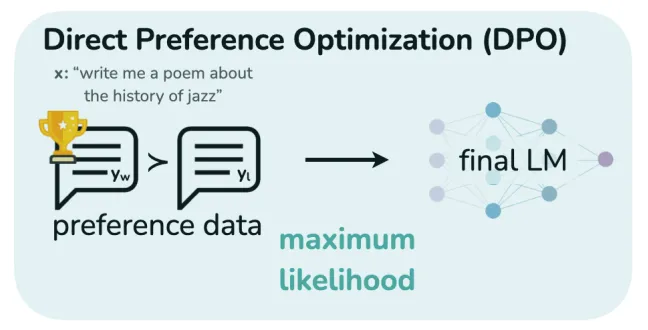
Việc thêm một KL constraint chính là điểm nhấn, ta hoàn toàn có thể thu được 1 policy lý tưởng để maximize KL-constrained rewards model:

$$\begin{aligned} &\max_{\pi} \mathbb{E}_{x \sim \mathcal{D}, y \sim \pi(y|x)} [r(x, y)] - \beta D_{KL}[\pi(y|x) \| \pi_{\text{ref}}(y|x)] \\ &= \max_{\pi} \mathbb{E}_{x \sim \mathcal{D}, y \sim \pi(y|x)} \left[ r(x, y) - \beta \log \left(\frac{\pi(y|x)}{\pi_{\text{ref}}(y|x)}\right) \right] \\ &= \min_{\pi} \mathbb{E}_{x \sim \mathcal{D}, y \sim \pi(y|x)} \left[ \log \left( \frac{\pi(y|x)}{\pi_{\text{ref}}(y|x)} \right) - \frac{1}{\beta} r(x, y) \right] \\ &= \min_{\pi} \mathbb{E}_{x \sim \mathcal{D}, y \sim \pi(y|x)} \left[ \log \frac{\pi(y|x)}{\frac{1}{Z(x)}\pi_{\text{ref}}(y|x)\exp \left( \frac{1}{\beta} r(x, y) \right)} - \log Z(x) \right] \end{aligned}$$

Trong đó ta có hàm partition:

$$Z(x) = \sum_y \pi_{\text{ref}}(y|x) \exp \left( \frac{1}{\beta} r(x, y) \right)$$

Điểm quan trọng nhất cần lưu ý là ta có thể thu được 1 phương trình cho một policy $\pi_r$, từ đó dễ tính được reward function $r$ dễ dàng:

$$\pi_r(y|x) = \frac{1}{Z(x)} \pi_{\text{ref}}(y|x) \exp \left( \frac{1}{\beta} r(x, y) \right).$$

Ta có thể ngay lập tức tính được $r$ như sau:

$$r(x, y) = \beta \log \left( \frac{\pi_r(y|x)}{\pi_{\text{ref}}(y|x)} \right) + \beta \log Z(x).$$

Trở lại phương trình optimal probability distribution, ta có thể viết lại sao cho mỗi trường hợp của $r$ được thay thế bằng phương trình trên:

$$p^*(y_1 \succ y_2 \mid x) = \frac{1}{1 + \exp \left( \beta \log \frac{\pi_{\text{ref}}(y_2|x)}{\pi_r(y_2|x)} - \beta \log \frac{\pi_{\text{ref}}(y_1|x)}{\pi_r(y_1|x)} \right)}.$$

Vẻ đẹp của phương trình này nằm ở chỗ không cần reward model để tối ưu policy theo probability distribution của human preference. Thay vào đó, ta có thể làm việc trực tiếp trên policy để cải thiện chính nó (đây chính là cơ sở của Direct Preference Optimization). Nhóm tác giả sử dụng các xác suất mà LLM tạo ra cho mỗi token để thực hiện finetune nó.

Cuối cùng, ta có hàm loss như sau:

$$\mathcal{L}_{DPO}(\pi_\theta; \pi_{\text{ref}}) = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}} \left[ \log \sigma \left( \beta \log \left( \frac{\pi_\theta(y_w|x)}{\pi_{\text{ref}}(y_w|x)} \right) - \beta \log \left( \frac{\pi_\theta(y_l|x)}{\pi_{\text{ref}}(y_l|x)} \right) \right) \right]$$

Hiện tại, ta có một phương trình so sánh các các xác suất giữa policy cũ ($\pi_{\text{ref}}$) và policy mới ($\pi_\theta$) cho một response được chọn ($y_w$) và một response không được chọn ($y_l$). Khi so sánh các xác suất này, nhiệm vụ của chúng ta là tối ưu hóa sao cho $y_w$ lớn hơn, có nghĩa là các policy đang trở nên tốt hơn trong việc đưa ra các response được chọn hơn là các response không được chọn.

Kết luận

Đầu tiên, DPO không yêu cầu sử dụng một reward model. Bạn chỉ cần dữ liệu chất lượng cao để mô hình có hiểu như nào là 1 response tốt và như nào là không tốt. Điều này giúp mô hình cải thiện mà không cần thêm bước huấn luyện phức tạp cho một reward model riêng biệt. Việc này không chỉ tiết kiệm thời gian mà còn giảm bớt nguồn lực và công sức cần thiết trong quá trình phát triển mô hình.

Thứ hai, DPO rất linh hoạt. Mỗi khi bạn sử dụng dữ liệu mới, DPO có khả năng thích nghi ngay lập tức nhờ vào cách mà nó xác định đúng hướng để đi (tức là biết được response như nào là ngon). Đây là một lợi thế lớn so với PPO, trong đó bạn phải huấn luyện lại reward model mỗi khi có dữ liệu mới. Với DPO, quá trình adapt diễn ra một cách tự động và hiệu quả, giúp tối ưu hóa kết quả nhanh chóng hơn.

Thứ ba, DPO cho phép bạn train mô hình không chỉ để biết cái gì là đúng mà còn biết cái gì là sai và không nên trả lời như thế. Điều này được thể hiện ở hàm loss, khi sử dụng cả ví dụ tốt và xấu, chúng ta đang dạy mô hình cách tránh các response không mong muốn cũng như cách hướng tới các response mong muốn. Điều này rất quan trọng vì một phần lớn của quá trình fine-tuning là giúp mô hình bỏ qua những chủ đề không quan trọng hoặc không phù hợp, và tập trung vào những gì quan trọng. Tính năng này của DPO trở nên đặc biệt hữu ích trong việc làm tăng performance mô hình trong cách tương tác và phản hồi.