[LLM 101] Thảo luận về finetune model LLM sử dụng LoRA (Low-Rank Adaptation)
Giới thiệu về LoRA
Các bạn đều biết rằng các LLM hiện nay đều có kích thước rất lớn và và việc cập nhật tất cả các tham số của mô hình trong quá trình training có thể rất tốn kém do giới hạn bộ nhớ GPU.
Ví dụ, giả sử chúng ta có một LLM với 7 tỷ tham số được biểu diễn trong một ma trận trọng số . (Thực tế, các tham số của mô hình được phân bổ qua nhiều ma trận khác nhau ở nhiều layer, nhưng để đơn giản, chúng ta chỉ đề cập đến một ma trận trọng số duy nhất tại đây). Trong quá trình back propagation, ta sẽ học được một ma trận , chứa thông tin về mức độ cần cập nhật các trọng số ban đầu để giảm thiểu hàm mất mát (loss function) trong quá trình huấn luyện.
Việc cập nhật trọng số được thực hiện như sau:
Nếu ma trận trọng số chứa 7 tỉ tham số, thì ma trận cập nhật trọng số cũng sẽ chứa 7 tỉ tham số => Việc tính toán ma trận có thể rất đòi hỏi về mặt tính toán và bộ nhớ.
Phương pháp LoRA ra đời nhằm phân rã (decompose) sự thay đổi trọng số (), thành một biểu diễn có rank thấp hơn. Cụ thể, phương pháp này không yêu cầu phải tính toán trực tiếp . Thay vào đó, LoRA học biểu diễn phân rã của trực tiếp trong quá trình training, và từ đó giúp ta tiết kiệm tài nguyên tính toán, các bạn có thể quan sát minh họa dưới đây.
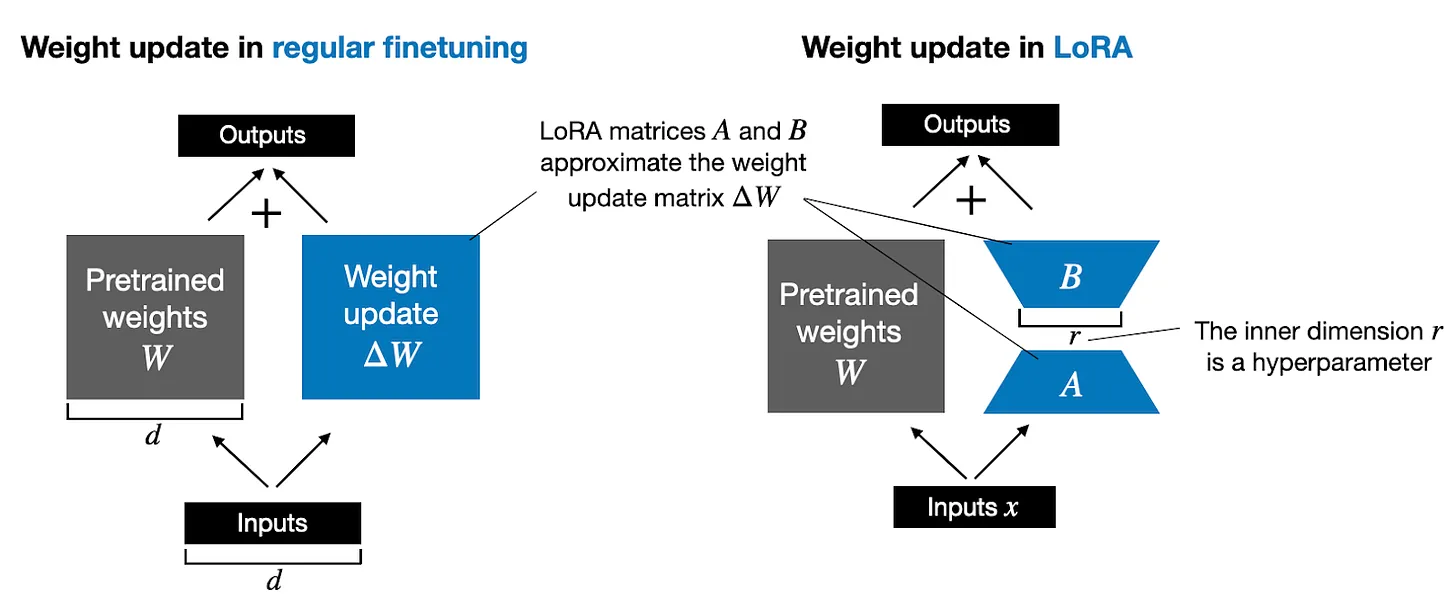
Như hình minh họa ở trên, việc phân tích có nghĩa là chúng ta biểu diễn ma trận lớn bằng hai ma trận LoRA nhỏ hơn, và . Nếu có số hàng bằng với và có số cột bằng với , ta có thể viết phân tích đó như sau: . (Đây là kết quả của phép nhân ma trận giữa và ).
Vậy việc này tiết kiệm bao nhiêu bộ nhớ? Điều này phụ thuộc vào rank , một siêu tham số. Ví dụ, nếu có 10,000 hàng và 20,000 cột, nó sẽ lưu trữ 200,000,000 tham số. Nếu chúng ta chọn và với , thì sẽ có 10,000 hàng và 8 cột, và sẽ có 8 hàng và 20,000 cột, tức là tham số, ít hơn khoảng 830 lần so với 200,000,000.
Tất nhiên, và không thể chứa toàn bộ thông tin mà có thể chứa  Khi sử dụng LoRA, giả thuyết của chúng ta là mô hình yêu cầu là một ma trận lớn với rank đầy đủ để nắm bắt tất cả kiến thức trong tập dữ liệu pretraining.
Khi sử dụng LoRA, giả thuyết của chúng ta là mô hình yêu cầu là một ma trận lớn với rank đầy đủ để nắm bắt tất cả kiến thức trong tập dữ liệu pretraining.
Tuy nhiên, khi finetune một LLM, chúng ta không cần thiết phải cập nhật tất cả trọng số mà chỉ cần học các thông tin cốt lõi và thể hiện chúng trong một lượng trọng số nhỏ hơn so với , do đó chúng ta có các cập nhật hạng thấp (low-rank) thông qua .
Một số đặc điểm của LoRA
Sự nhất quán
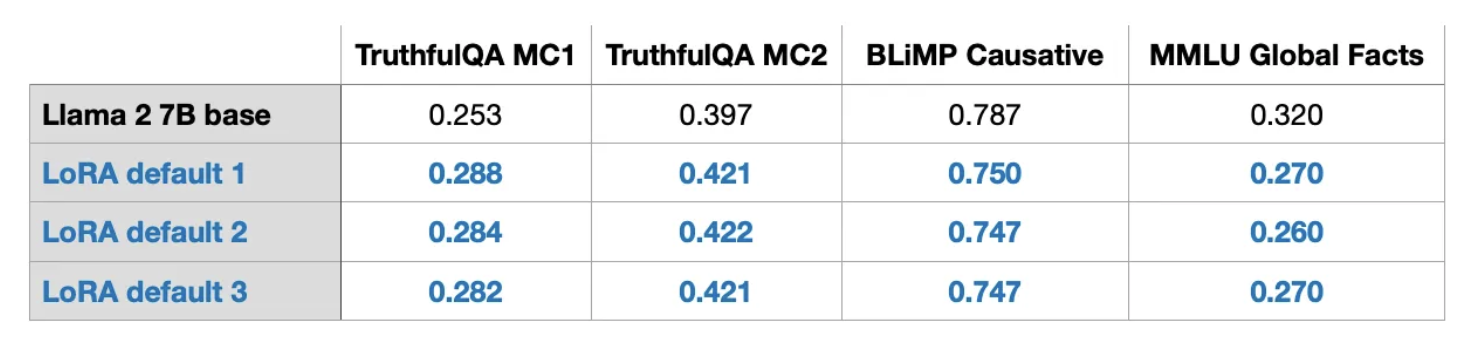
Khi thực hiện thí nghiệm với LoRA, ta có thể thấy các kết quả benchmark đạt được rất nhất quán giữa các lần chạy khác nhau dù trong quá trình training luôn có sự ngẫu nhiên hoặc khi huấn luyện các mô hình trên GPU nói chung. Đây là một cơ sở tốt để tiến hành các nghiên cứu so sánh bổ sung.
Sự ổn định này cho thấy phương pháp LoRA có thể duy trì hiệu suất ổn định giữa các lần training, giảm thiểu tác động của yếu tố ngẫu nhiên. Điều này không chỉ giúp cải thiện độ tin cậy của kết quả mà còn tạo điều kiện thuận lợi cho việc so sánh các phương pháp khác nhau một cách công bằng và chính xác hơn.
Sự đánh đổi giữa thời gian training và bộ nhớ GPU sử dụng
QLoRA, viết tắt của quantized LoRA, là một kỹ thuật nhằm giảm việc sử dụng nhiều bộ nhớ trong quá trình finetuning. Trong quá trình backpropagation, QLoRA lượng tử hóa (quantize) các trọng số đã được pretrained xuống mức chính xác 4-bit (4-bit precision) và sử dụng paged optimizers để xử lý các đỉnh bộ nhớ.
Về cơ bản, ta có thể tiết kiệm được 33% bộ nhớ GPU khi sử dụng QLoRA. Tuy nhiên, điều này đi kèm với việc tăng 39% thời gian training do các bước quantization và giải quantization bổ sung của các trọng số pretrained trong QLoRA.
Dưới đây là so sánh giữa LoRA mặc định với độ chính xác floating point 16-bit và QLoRA với độ chính xác 4-bit Normal Floats:
-
LoRA mặc định với 16-bit floating point:
- Thời gian huấn luyện: 1.85 giờ
- Bộ nhớ sử dụng: 21.33 GB
-
QLoRA với 4-bit Normal Floats:
- Thời gian huấn luyện: 2.79 giờ
- Bộ nhớ sử dụng: 14.18 GB
Mặc dù có sự khác nhau trên nhưng hiệu suất mô hình hầu như không bị ảnh hưởng, điều này làm cho QLoRA trở thành một lựa chọn khả thi thay thế cho phương pháp training LoRA thông thường. Từ đó, giải quyết được các vấn đề về sử dụng quá bộ nhớ GPU 
Điều này nghĩa là mặc dù QLoRA mất thêm thời gian huấn luyện nhưng nó mang lại lợi ích quan trọng về việc tiết kiệm bộ nhớ, điều này rất hữu ích cho các hệ thống với hạn chế về tài nguyên GPU.
Learning Rate Schedulers
Learning rate schedulers được sử dụng để giảm dần giá trị learning rate trong suốt quá trình huấn luyện nhằm tối ưu hóa sự hội tụ và tránh hiện tượng overshooting khi đạt đến điểm cực tiểu của hàm mất mát.
Cosine annealing là một phương pháp điều chỉnh learning rate theo đường cong cosine. Nó bắt đầu với một learning rate cao, sau đó giảm dần một cách mượt mà  gần như về 0 theo dạng đồ thị cosine. Một biến thể phổ biến của phương pháp này là half-cycle variant, trong đó chỉ hoàn thành một nửa chu kỳ của hàm cosine trong suốt quá trình huấn luyện, như được minh họa trong hình dưới đây.
gần như về 0 theo dạng đồ thị cosine. Một biến thể phổ biến của phương pháp này là half-cycle variant, trong đó chỉ hoàn thành một nửa chu kỳ của hàm cosine trong suốt quá trình huấn luyện, như được minh họa trong hình dưới đây.
Việc thêm lịch trình cosine annealing vào code finetuning của LoRA có thể cải thiện hiệu suất của SGD đáng kể. Tuy nhiên, phương pháp này có ảnh hưởng ít hơn đối với các optimizer như Adam và AdamW.
Dưới đây là hình ảnh minh họa cho quá trình điều chỉnh learning rate theo hàm cosine:
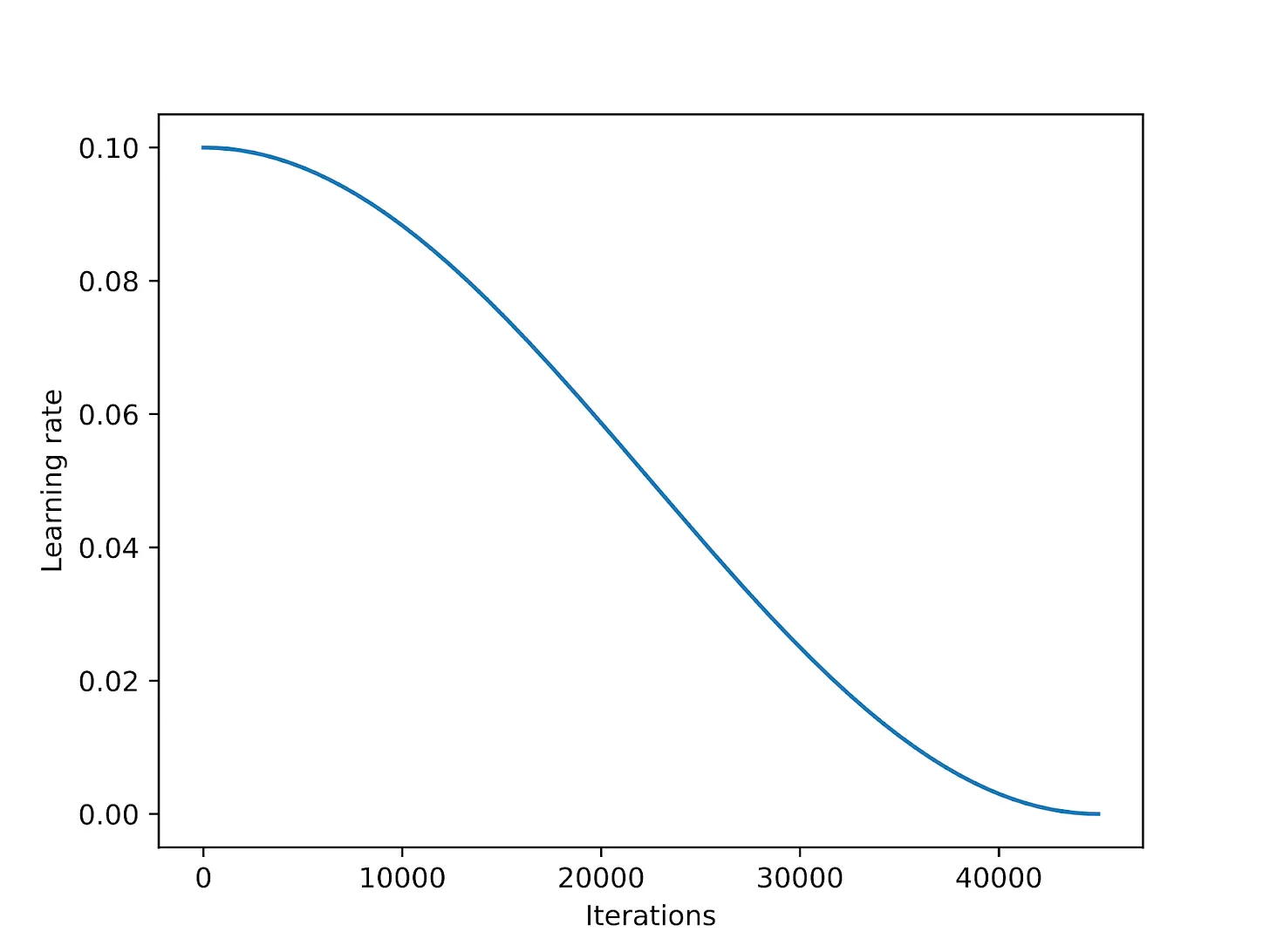
Hình trên cho thấy cách mà learning rate bắt đầu từ mức cao và giảm dần theo dạng cosine qua nhiều lần lặp (iterations).
Việc sử dụng cosine annealing giúp cho quá trình huấn luyện trở nên ổn định hơn với SGD bằng cách giảm learning rate một cách mượt mà hơn so với các Learning Rate Schedulers khác, do đó giúp đạt được hội tụ hiệu quả hơn. Tuy nhiên, đối optimizer phức tạp hơn như Adam và AdamW thì lại không hiệu quả do các chiến lược cập nhật trọng số khác nhau của chúng đã giúp kiểm soát learning rate một cách thông minh hơn 
Nên finetune với bao nhiêu epoch?
Thông thường, khi huấn luyện các mạng CNNs, chúng ta chạy hàng trăm epoch huấn luyện. Vậy training nhiều epoch có hữu ích cho instruction finetuning hay không?
Khi tăng số lượng epoch cho tập dữ liệu instruction finetuning Alpaca gồm 50,000 sample lên gấp đôi (tương đương với 2 epoch huấn luyện), ta có thể nhận thấy một sự giảm sút trong hiệu suất của mô hình.
Dưới đây là bảng so sánh hiệu suất:
| TruthfulQA MC1 | TruthfulQA MC2 | BLiMP Causative | MMLU Global Facts | |
|---|---|---|---|---|
| AdamW + QLoRA + scheduler | 0.282 | 0.423 | 0.783 | 0.270 |
| 2x more iterations | 0.280 | 0.415 | 0.778 | 0.270 |
Kết luận rút ra từ thử nghiệm trên là việc huấn luyện nhiều epoch có thể không có lợi cho instruction finetuning, thậm chí có thể làm suy giảm chất lượng kết quả. Bên cạnh đó, hiệu suất cũng giảm tương tự khi áp dụng trên tập dữ liệu LIMA với 1,000 sample. Sự suy giảm này có khả năng do hiện tượng overfitting.
Lý do có thể là khi huấn luyện nhiều epoch, mô hình bắt đầu học thuộc lòng các đặc điểm của tập dữ liệu huấn luyện thay vì học các khái niệm tổng quát  Đặc biệt đối với các mô hình instruction finetuning, mục tiêu là để mô hình học được khả năng suy luận và hiểu biết chỉ từ một tập dữ liệu hạn chế, do đó việc huấn luyện quá lâu có thể dẫn đến overfitting và làm giảm khả năng tổng quát hóa của mô hình trên các tập dữ liệu mới.
Đặc biệt đối với các mô hình instruction finetuning, mục tiêu là để mô hình học được khả năng suy luận và hiểu biết chỉ từ một tập dữ liệu hạn chế, do đó việc huấn luyện quá lâu có thể dẫn đến overfitting và làm giảm khả năng tổng quát hóa của mô hình trên các tập dữ liệu mới.
Nên chọn optimizer là Adam hay SGD?
Các optimizer Adam và AdamW vẫn là các lựa chọn phổ biến trong deep learning mặc dù chúng yêu cầu rất nhiều bộ nhớ khi làm việc với các mô hình lớn. Nguyên nhân là do các optimizer này duy trì 2 giá trị trung bình động cho mỗi tham số của mô hình: trung bình của gradient (moments bậc nhất) và trượt phương sai (moments bậc hai) của gradient.
Nói cách khác, optimizer Adam lưu trữ hai giá trị bổ sung cho mỗi tham số của mô hình trong bộ nhớ. Nếu chúng ta làm việc với một mô hình có 7 tỷ tham số, điều đó có nghĩa là phải theo dõi thêm 14 tỷ tham số trong quá trình huấn luyện. Ngược lại, các optimizer SGD không cần theo dõi bất kỳ tham số bổ sung nào trong quá trình huấn luyện.
Tuy nhiên, khi huấn luyện một mô hình Llama 2 với 7 tỷ tham số bằng AdamW và các giá trị mặc định của LoRA () cần 14.18 GB bộ nhớ GPU. Huấn luyện cùng mô hình đó với SGD chỉ cần 14.15 GB bộ nhớ GPU. Nói cách khác, lượng bộ nhớ tiết kiệm được (0.03 GB) là rất nhỏ.
Tại sao lại như vậy? Đó là vì với LoRA, ta chỉ có một số lượng nhỏ các tham số có thể huấn luyện. Chẳng hạn, nếu , chúng ta có 4,194,304 tham số có thể huấn luyện được trong tổng số 6,738,415,616 tham số của một mô hình Llama 2 với 7 tỷ tham số.
Nếu chỉ nhìn vào các con số thô, 4,194,304 tham số có thể huấn luyện được vẫn nghe có vẻ nhiều, nhưng nếu tính toán, chúng ta chỉ có:
Sự khác biệt là 0.03 GB = 30 MB do có thêm chi phí bổ sung trong việc lưu trữ và sao chép trạng thái của optimizer. Số 2 đại diện cho số lượng các tham số bổ sung mà Adam lưu trữ, và 16-bit chỉ đến độ chính xác mặc định cho trọng số mô hình.
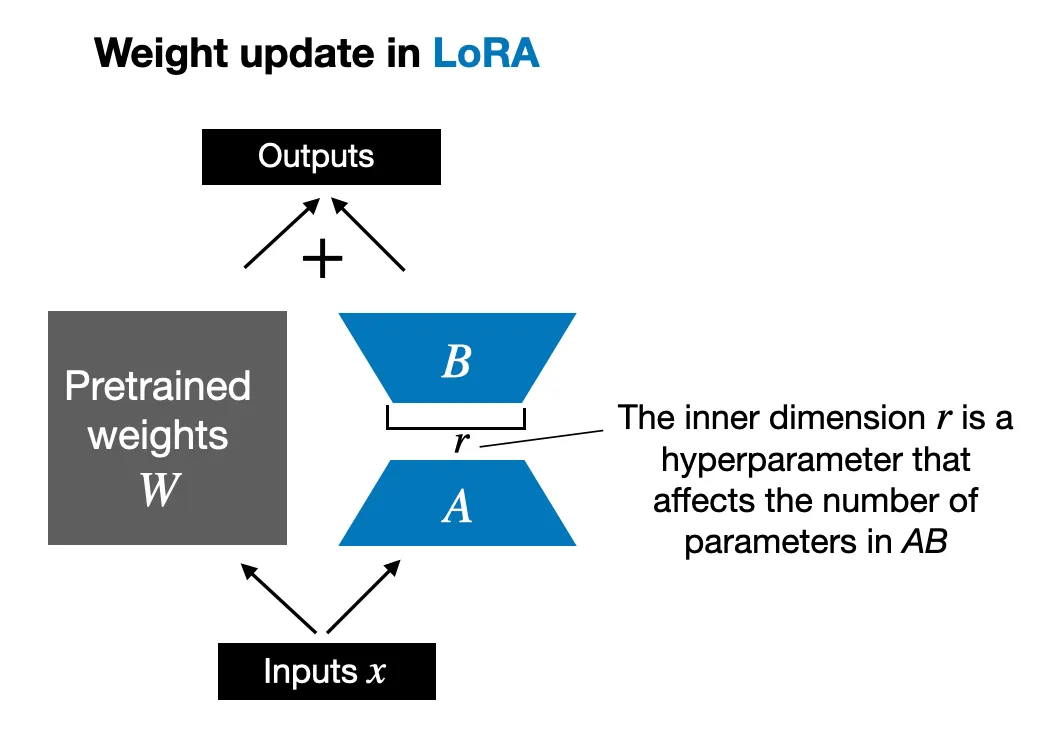
Hình trên minh họa cách cập nhật trọng số trong LoRA, với kích thước là một siêu tham số ảnh hưởng đến số lượng các tham số trong .
Tuy nhiên, nếu chúng ta tăng của LoRA lên 256, sự khác biệt giữa các optimizer Adam và SGD trở nên đáng chú ý hơn:
- 17.86 GB với AdamW
- 14.46 GB với SGD
Kết luận rút ra từ đây là việc chuyển các optimizer Adam sang SGD có thể không có nhiều giá trị khi của LoRA nhỏ. Tuy nhiên, ta có thể tiết kiệm VRAM cho GPU đáng kể khi tăng giá trị 
Áp dụng LoRA cho nhiều layer hơn
Trong các thử nghiệm trên, LoRA chỉ được kích hoạt cho các ma trận trọng số Key và Value trong mỗi layer transformer. Tuy nhiên, chúng ta cũng có thể kích hoạt LoRA cho các ma trận trọng số Query, các layer projection, các layer tuyến tính khác giữa các block multi-head attention, và layer linear cuối cùng.
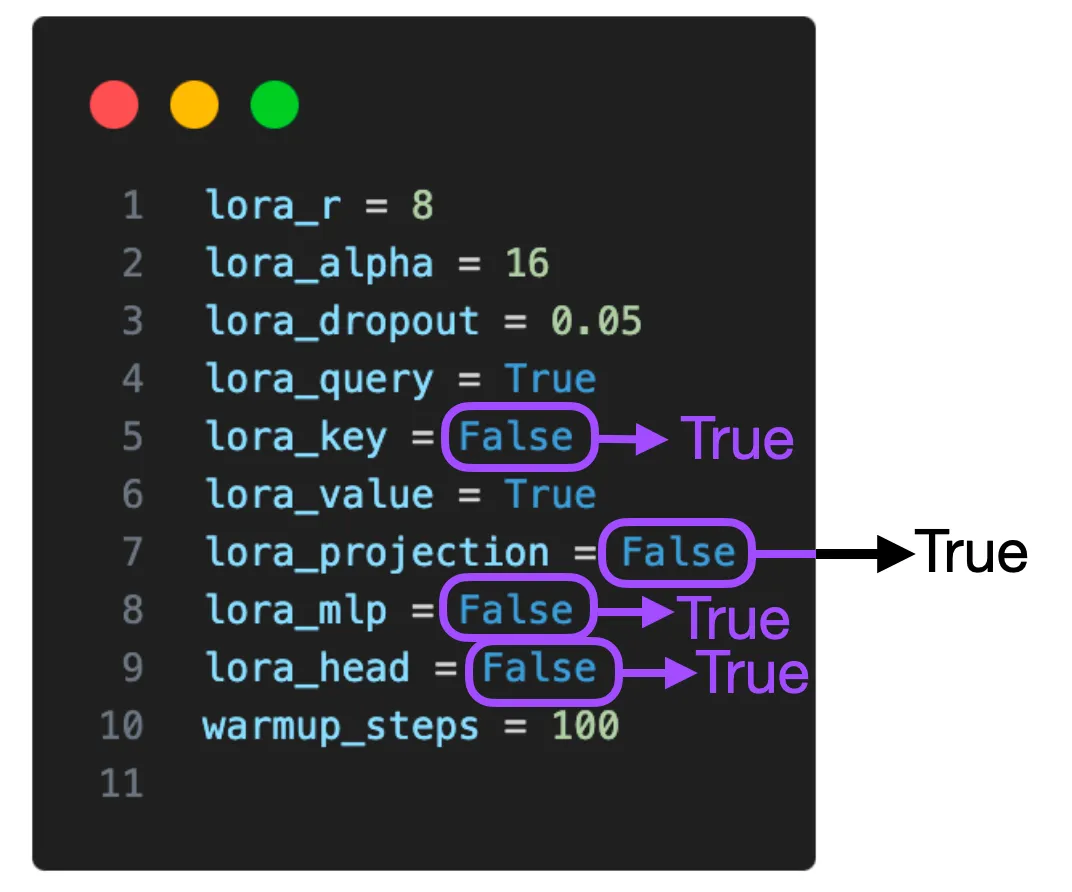
Trong hình minh họa trên, ta có thể thấy cấu hình LoRA cho một mô hình. Hiện tại, các tham số như lora_query, lora_key, lora_value, lora_projection, lora_mlp, và lora_head đều có thể được bật. Khi kích hoạt LoRA cho tất cả các layer này, số lượng các tham số có thể train tăng lên đáng kể, cụ thể là từ 4,194,304 lên 20,277,248, tăng gấp 5 lần cho mô hình Llama 2 với 7 tỷ tham số. Điều này cũng yêu cầu dung lượng bộ nhớ lớn hơn (16.62 GB thay vì 14.18 GB), nhưng điều này có thể cải thiện đáng kể hiệu suất mô hình.
Bảng kết quả dưới đây so sánh hiệu năng của mô hình khi sử dụng AdamW kết hợp với QLoRA và scheduler, so với khi kích hoạt QLoRA cho tất cả các layer. Các chỉ số đo lường hiệu năng trên các tập dữ liệu như TruthfulQA MC1, TruthfulQA MC2, BLiMP Causative, và MMLU Global Facts cho thấy rằng việc kích hoạt QLoRA cho toàn bộ layer có thể mang lại hiệu suất tốt hơn.

Tuy nhiên, một hạn chế của thí nghiệm này là ta chỉ thử nghiệm 2 config chính: (1) chỉ kích hoạt LoRA cho các ma trận trọng số Query và Value, và (2) kích hoạt LoRA cho tất cả các lớp. Sẽ ok hơn nếu test các kết hợp khác trong các thử nghiệm khác  , chẳng hạn như việc kích hoạt LoRA cho layer projection có làm tăng hiệu suất hay không.
, chẳng hạn như việc kích hoạt LoRA cho layer projection có làm tăng hiệu suất hay không.
Nhìn chung, việc finetune các block LoRA trên nhiều layer khác nhau là một hướng nghiên cứu tiềm năng để tối ưu hóa hiệu năng của các mô hình transformer lớn.
Lựa chọn các hyperparameter của LoRA là R và Alpha như nào?
Bài báo gốc về LoRA đã nêu rõ rằng LoRA đưa vào một hệ số tỉ lệ để áp dụng các trọng số LoRA vào các trọng số đã huấn luyện trong quá trình feed forward. Hệ số tỉ lệ này liên quan đến tham số rank , như đã thảo luận trước đó, cùng với một hyperparamer khác là được áp dụng theo công thức:
Như ta thấy trong công thức ở trên, tỉ lệ scaling càng lớn thì ảnh hưởng của các trọng số LoRA càng đáng kể.
Trong các thử nghiệm trước đây, giá trị và đã được sử dụng, kết quả là ta có 2-fold scaling. Quy tắc chọn bằng hai lần thường là theo kinh nghiệm thôi  khi sử dụng LoRA cho các mô hình LLMs, nhưng liệu điều này có đúng với các giá trị lớn hơn không?
khi sử dụng LoRA cho các mô hình LLMs, nhưng liệu điều này có đúng với các giá trị lớn hơn không?
Trong bảng kết quả dưới đây, các thí nghiệm với những config khác nhau cho và được trình bày. Đặc biệt, trong sự kết hợp cụ thể của mô hình và tập dữ liệu này, khi và (tỉ lệ scaling 0.5 lần) thì hiệu năng thậm chí còn tốt hơn.
Một điểm thú vị là kết quả cho thấy rằng việc chọn thường dẫn đến kết quả tốt nhất, nhưng cũng có thể không gây hại gì nếu thử nghiệm với các tỉ lệ khác nhau.
Kết quả thử nghiệm với mô hình Llama 2 có 7B tham số:
| Thiết lập LoRA | TruthfulQA MC1 | TruthfulQA MC2 | BLiMP Causative | MMLU Global Facts |
|---|---|---|---|---|
| All-layer QLoRA, r=8, α=16 | 0.302 | 0.441 | 0.788 | 0.260 |
| r=256, α=1024 | 0.269 | 0.407 | 0.746 | 0.247 |
| r=256, α=512 | 0.304 | 0.466 | 0.746 | 0.320 |
| r=256, α=256 | 0.308 | 0.460 | 0.738 | 0.300 |
| r=256, α=128 | 0.328 | 0.484 | 0.757 | 0.280 |
| r=256, α=64 | 0.321 | 0.473 | 0.655 | 0.260 |
| r=256, α=32 | 0.294 | 0.506 | 0.475 | 0.180 |
| r=256, α=1 | 0.283 | 0.411 | 0.758 | 0.240 |
Nhìn vào bảng trên, ta thấy rằng việc điều chỉnh các giá trị và có thể ảnh hưởng đáng kể đến hiệu năng của mô hình. Điều này gợi ý rằng, mặc dù chọn là một quy tắc tốt, nhưng việc khám phá các tỉ lệ khác nhau cũng là cần thiết để đạt được hiệu năng tối ưu trong các tình huống khác nhau.
Kết luận
Việc sử dụng LoRA để finetune các mô hình LLM lớn mang lại nhiều lợi ích rõ rệt như sau:
- Tiết kiệm tài nguyên: Dùng ít tài nguyên phần cứng hơn, giúp giảm chi phí và mở rộng khả năng tiếp cận.
- Hiệu quả và tối ưu: Hiệu quả cao (tất nhiên là nếu bạn config tham số hợp lý
 ) mà không cần nhiều đến cấu hình phần cứng.
) mà không cần nhiều đến cấu hình phần cứng. - Nhanh chóng và khả thi: Thời gian huấn luyện ngắn và yêu cầu bộ nhớ trong tầm giới hạn của GPU.
All rights reserved