Linear regression với Gradient Descent

TL;DR

Giới thiệu thuật toán Linear Regression, làm quen với Linear regression trong thư viện Sklearn, và cuối cùng là tự tay cài đặt thuật toán này bằng numpy.

Toàn bộ code cho bày này bạn đọc có thể tìm thấy ở file Jupyter Notebook trên github.

Linear regression là gì?

Trước tiên, mời bạn thử trả lời một câu hỏi sau: một người ném lần lượt 4 viên bi, 3 viên bi đầu được ném ra có vị trí như hình dưới, hỏi viên thứ 4 được ném ra có thể nằm ở đâu?

Có 3 vị trí được đánh đáu là xanh lá cây ở trên cùng, xanh da trời ở giữa hình, và đỏ ở dưới cùng. Thực hiện đự đoán và lựa chọn đáp án bạn cho là hợp lý nhất?

Nếu bạn đã thực hiện dự đoán, và bất kể bạn lựa chọn đáp án gì thì việc bạn xem xét vị trí của 3 viên bi để đưa ra mối quan hệ giữa chúng, và dự đoán viên bi thứ 4 theo mối quan hệ đó, là một hành động regression.

Và nếu bạn dự đoán viên bi thứ 4 nằm ở "B. vị trí xanh nước biển" bởi vì 3 viên bi đầu trông có vẻ nằm gần 1 đường thẳng, viên bi thứ 4 chắc theo quy luật đó thì bạn vừa làm một hành động Linear regression.

Linear là khái niệm chỉ sự tuyến tính, trong mặt phẳng thì đó là đường thẳng, trong không gian 3 chiều thì đó là mặt phẳng và trong không gian nhiều chiều thì đó là mặt siêu phẳng.

Vậy bạn có thể hiểu rằng, Linear Regression là một model, model đó áp dụng trên dữ liệu có tính chất linear, có thể đưa ra dự đoán có tính chất linear.

Như đã nhắc đến ở bài trước, khi nói đến machine learning (ML) thì phải nhắc đến data. Do data có tính chất linear nên mới sử dụng Linear Regression Model. Hay Linear Regression model được sinh ra để mô hình hóa dữ liệu vố có tính chất linear.

Trong hộp chức năng chứa các công cụ ML, Linear Regression là 1 công cụ trong đó, nó giúp dự đoán con số, số lượng.

Ở các phần tiếp theo đây, tôi sẽ đưa ra ví dụ cụ thể về data và bài giải toán dự đoán sử dụng linear regression.

Linear regression sử dụng thư viện Sklearn

Thư viện Sklearn là thư viện python phổ biến cài đặt sẵn các thuật toán Machine Learning. Sklearn cho phép người dùng nhanh chóng làm việc với model mà không cần phải cài đặt lại từ đầu.

Có thể coi linear regression của sklearn là một công cụ vì khi chưa biết gì về Linear Regression, ta có thể coi như nó là một chiếc hộp đen có chức năng và vẫn sử dụng được.

Đầu tiên, chúng ta sử dụng công cụ này của thư viện sklearn giúp bạn làm quen với vấn đề và hiểu Linear regression giúp được gì trước.

Ba bước để dụng model của thư viện sklearn:

• Tạo instance của model mà ta muốn sử dụng, chẳng hạn LinearRegression gọi tắt instance này là model.
• Fit dữ liệu train cho model để model học.
• Predict (dự đoán) thực hiện dự đoán trên dữ liệu mới

Ngoài 3 bước trên, ta còn có thể kiểm tra độ chính xác model đã train, lấy ra tham số đã học, vv.

Ví dụ 1: dự đoán hàm số $y=-3x+5$ bằng Sklearn

Bài toán: Xét trên mặt phẳng 2D, giả sử bây giờ ta có tập hợp rất nhiều điểm nằm trên một đường thẳng, cùng với các điểm nhiễu nên nằm lệch đường thẳng một chút. Tìm phương trình đường thẳng đó?

Phân tích: Rõ ràng không có 1 đường thẳng nào đi qua hết các điểm đó. Tuy nhiên, ta có thể quy về bài toán tìm đường thẳng tốt nhất có thể. Tốt nhất ở đây là sự thỏa mãn yêu cầu nào đó, chẳng hạn trung bình khoảng cách từ các điểm đến đường thẳng là nhỏ nhất.

Giải quyết: Bài toán này có thể giải bằng công cụ Linear regression, trong đó, data là tập các điểm đã cho. Linear regression model sẽ học trên data để tìm ra hệ số của đường thằng.

Ở phần này, tôi sẽ dùng đường thẳng $y = -3x + 5$ để tạo 300 điểm dữ liệu có chứa nhiễu. Sau đó tôi sử dụng công cụ thư viện sklearn học trên các điểm dữ liệu đã tạo ra đó, để xem nó có thể tìm ra đường thẳng $y=-3x+5$ này không.

Tạo dữ liệu:

'''
Bộ dữ liệu: y = -3x + 5 chứa nhiễu
'''
np.random.seed(3)
X = np.random.rand(300, 1)
y = -3 * X + 5 + 0.3*np.random.randn(300, 1) # thêm nhiễu vào
# Visualize data 
plt.plot(X, y, 'bo')
plt.show()

Ta sẽ chia bộ data này thành 2 phần, 1 phần để train model, phần còn lại để test model.

X_train, X_test, y_train, y_test = train_test_split(X, y)

Ta tạo một instance của Linear Regression Model, sau đó train model bằng hàm fit():

# sử dụng model LinearRegresion từ thư viện Sklearn
model = LinearRegression()
# thực hiện train dữ liệu trên tập train
model.fit(X_train, y_train)

Việc thực hiện dự đoán bằng cách gọi hàm predict() và tính sai số của dự đoán bằng metric MSE:

# thực hiện dự đoán trên tập test
y_hat = model.predict(X_test)
# hiển thị MSE của dự đoán so với label
mean_squared_error(y_test, y_hat)

Ở đây, MSE giống như một cách để ta kiểm tra xem đường thẳng mà model dự đoán có như ta mong muốn hay không. Cụ thể, Mean Squared Error là metric để tính sai số giữa 2 số, giữa 2 vector, hay 2 tensor có cùng kích thước, Ví dụ:

• dự đoán của ta là 1 trong khi giá trị đúng phải là 3 thì $mse = (1-3)^2 = 4$
• nếu nhiều hơn 1 dự đoán chẳng hạn dự đoán lần lượt là 3, 4 trong khi giá trị thực là 2, 1 thì ta chú ý lấy trung bình cộng $mse = 1/2*[(3-2)^2 + (4-1)^2] = 5$

Bạn đọc có thể xem công thức toán học tổng quát của MSE ở phần sau. Bây giờ, ta vẽ lại kết quả dữ liệu test thực tế và dữ liệu test model dự đoán được để xem trực quan đường thẳng mà model đã dự đoán:

# Vẽ đồ thị dữ liệu test (xanh) và đường dự đoán (đỏ)
plt.scatter(X_test, y_test)
plt.plot(X_test, y_hat, 'r')
plt.show()

kết quả:

Nhận xét: đường thẳng đi xuyên qua các điểm dữ liệu, có phương gần với phương phân bố của các điểm dữ liệu.

In ra hệ số mà model đã học được:

# in weight học được w1, w0
print(model.coef_, model.intercept_)

Kết quả là: $-3.04802998, 5.02350025$ trong khi hàm ta cần tìm $y = -3x +5 $ có hệ số là $-3, 5$.

Kết luận: Vậy là model đã học và tìm ra được gần chính xác tham số cần tìm.

Ví dụ 2: dự đoán giá nhà Boston bằng Sklearn

Bộ data giá nhà ở thành phố Boston là bộ data quen thuộc khi học Machine Learning. Đây là một bộ dữ liệu thực tế bao gồm thông tin về các ngôi. Mỗi ngôi nhà sẽ có thông tin về số phòng, năm xây dựng, cả giá, vân vân.

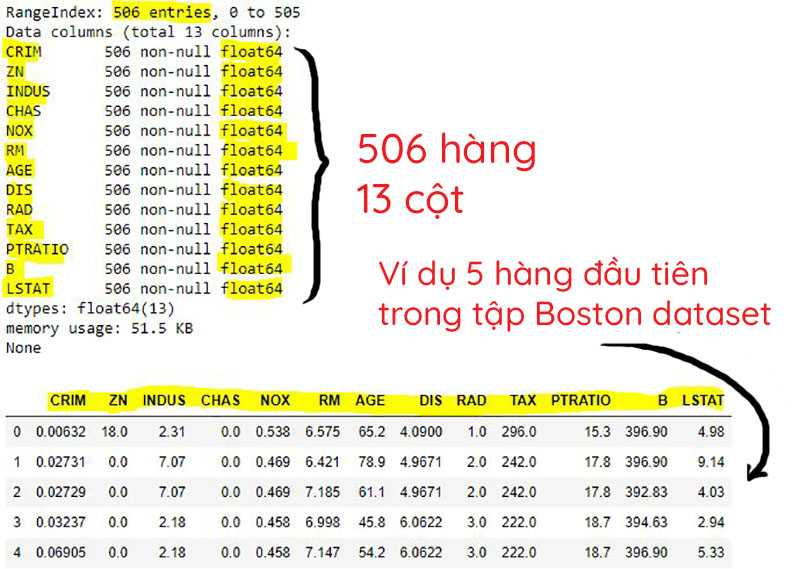
xem thêm miêu tả về bộ data này, cũng như cách làm việc với nó ở đây.

Ở đây giá nhà là thứ ta qua tâm nhất bởi nó có ý nghĩa về mặt kinh tế và có thể được tính toán từ các thông tin khác. Do đó, ta chọn giá nhà là đầu ra cần dự đoán, các thông tin khác có thể được chọn là đầu vào.

Bài toán: Cho thông tin ngôi nhà ở Boston, dự đoán giá nhà của nó?

Phân tích: Trong ví dụ này, để có thể biểu diễn trực quan bằng đồ thị 2D, tôi chỉ xét 1 thông tin duy nhất của ngôi nhà để đoán giá. Bạn đọc cũng có thể sử dụng nhiều thông tin kết hợp để đoán giá.

Khởi tạo đầu vào, đầu ra $X, y$. $X$ là thông tin về ngôi nhà, $y$ là giá nhà. Ta vẽ biểu đồ $X, y$ trên mặt phẳng 2D để có cái nhìn tổng quan về data:

boston_data = load_boston()
X = boston_data.data[:, 5, np.newaxis]   # trường thứ 5 là RM (số phòng)
y = boston_data.target[:, np.newaxis]    # taget là giá nhà

# Visualize data 
plt.plot(X, y, 'bo')
plt.xlabel('RM')
plt.ylabel('PRICE')
plt.show()

Nhận xét: dữ liệu có hơi hơi tính chất linear, khi số phòng tăng, giá nhà tăng theo. Bên cạnh đó, có những điểm dữ liệu không theo quy luật đó (outlier) tuy nhiên không nhiều.

Giải quyết: Ta có thể áp dụng Linear Regression model vào tập data này. Model linear regression sẽ không cho ta giá chính xác của một căn nhà dựa vào số phòng, nhưng nó sẽ làm tốt việc đoán giá một ngôi nhà có X phòng thường thì giá khoảng bao nhiêu?

Giống như ví dụ trước, việc đầu tiên là ta chia dữ liệu train, test.

# trước hết cần scale data để tránh trường hợp số lớn làm tràn phép tính
scalerx = StandardScaler()
scalery = StandardScaler()
X_scaled = scalerx.fit_transform(X)
y_scaled = scalery.fit_transform(y)

# chia dữ liệu thành tập train và tập test
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y_scaled)

Tạo một instance của model Linear Regression và train model bằng hàm fit().

# lấy model LinearRegression từ thư viên SKlearn
model = LinearRegression()
# thực hiện train model trên tập train
model.fit(X_train, y_train)

Thực hiện dự đoán trên tập test để xem model hoạt động tốt không:

# thực hiện train model trên tập test
y_hat = model.predict(X_test)

# tính sai số lỗi MSE của dự đoán so với thực tế trên tập test
mse = mean_squared_error(y_hat, y_test)
print(mse)

Vẽ biểu đồ thể hiện dự đoán bở model của ta:

# hiển thị đồ thị dữ liệu test (xanh) và đường dự đoán đã học được (đỏ)
plt.scatter(scalerx.inverse_transform(X_test), scalery.inverse_transform(y_test))
plt.plot(scalerx.inverse_transform(X_test), scalery.inverse_transform(y_hat), 'r')
plt.xlabel('House feature: RM')
plt.ylabel('Price')
plt.show()

In weight mà model đã học được:

# in weight w0, w1 mà model của sklearn đã học w1, w0
print(model.coef_, model.intercept_)

Kết quả nhận được là 0.71904031, 0.0025078. Vậy giá nhà tại Boston với số phòng đa số theo mối quan hệ $ giá nhà = 0.71904031 * số phòng + 0.0025078 $

Kết luận: model đã học được từ giữ liệu giá nhà và cho ra model biểu diễn được mối quan hệ giữa thông tin nhà (số phòng) và giá.

Tới đây, chúng ta đã hiểu được bài toán cũng như đầu vào đầu ra thông qua việc sử dụng tool có sẵn (LinearRegression của thư viện sklearn).

Ngay sau đây, bạn đọc đã có thể tự mình tạo model và thử với các thông tin khác của ngôi nhà, xem sai số dự đoán và so sánh kết quả đó với kết quả mà tôi đã làm với thông tin RM (số phòng).

Nếu bạn đọc đã hiểu Linear regression là cái gì rồi nhưng chưa biết chuyện gì đã xảy ra đằng sau model này thì mời bạn sang phần tiếp theo.

Tự viết thuật toán Linear Regression không dùng thư viện Sklearn

Để hiểu hơn về Linear regression, ta sẽ đào sâu hơn một chút bằng cách code lại model Linear regression.

"What I cannot create, I do not understand" _Richard Feynman

Ta sẽ mô hình hóa toàn bộ bài toán bằng toán học, giải quyết nó trên lý thuyết toán, cuối cùng là cài đặt trên máy tính.

Phân tích toán học

Bài toán linear regresion tóm lại là bài toán tìm đường thằng/mặt phẳng/siêu mặt phẳng tùy hàm số toán học thể hiện đầu ra là hàm đơn biến/hai biến/đa biến. Tổng quát hóa, ta có hàm số đầu ra $\hat{y}$ như sau:

$$\hat{y} = bias + x_1*w_1 + x_2*w_2 + .. + x_n*w_n$$

Công cụ matrix calculus cho phép chúng ta biểu diễn ngắn ngọn dễ nhìn hơn bằng vector và ma trận như sau:

Đặt vector $\bar{\textbf{x}} = [1, x_1, x_2, x_3, ..., x_n]$, và $\textbf{w}=[bias, w_1, w_2, w_3, ..., w_n]^{T}$. Lúc này công thức trên sẽ được biểu diễn là:

$$\hat{y} = \bar{\textbf{x}}\textbf{w}$$

Để đầu ra như ta mong muốn, cần phải có một metric để đánh giá giữa đầu ra dự đoán $\hat{y}$ và đầu ra thực thế $y$. MSE mà ta đã làm quen ở trên chính là metric đó. MSE được tính trên toàn bộ tập train. Vì thế trong công thức sau đây, ta dùng $y_i, \hat{y_i}$ để biểu diễn cặp giá đầu ra đúng và giá trị đầu ra dự đoán của model ở mẫu thứ i trong N mẫu của tập train.

$$mse=\frac{1}{2N}\sum_{i=1}^{N}(y_i-\hat{y_i})^2$$

Lưu ý: hệ số 2 ở mẫu số không làm ảnh hưởng đến nghiệm nên ta thêm vào để dễ tính toán.

Thay dự đoán $\hat{y_i}$ bằng biểu diễn $\bar{\textbf{x}}\textbf{w}$ vào, lúc này mse tương đương với:

$$mse=\frac{1}{2N}\sum_{i=1}^{N}(y_i-\bar{\textbf{x}_i}\textbf{w})^2$$

Ta mong muốn model học chính xác nhất có thể, nghĩa là dự đoán $\hat{y}$ sát với $y$. Điều này cũng có nghĩa là mse phải là nhỏ nhất. Xét trên tập train, rõ ràng $y_i, \bar{\textbf{x}_i}$ của hàm số mse là cố định. Do đó, để mse đạt nhỏ nhất, ta phải thay đổi $\textbf{w}$.

Coi $\textbf{w}$ là biến số, ta đặt hàm số loss theo biến số là $\mathbf{w}$ đối với mse như sau:

$$\mathcal{L}(\mathbf{w}) = \frac{1}{2N}\sum_{i=1}^{N}(y_i - \bar{\mathbf{x_i}}\mathbf{w})^2$$

Việc tìm nghiệm cực tiểu của mse bây giờ trở thành tìm giá trị $\mathbf{w}$ sao cho làm loss đạt cực tiểu.

$$\mathbf{w^*} = \arg\min_{\mathbf{w}}\mathcal{L}(\mathbf{w})$$

Phương trình trên, đôi khi có thể giải bằng phương pháp giải phương trình đạo hàm của hàm loss bằng 0, đôi khi không thể vì đạo hàm quá phức tạp. May thay, model chúng ta đang xem xét có phương trình tuyến tính nên có thể tìm nghiệm được bằng cách đó. Sau khi tìm ra các nghiệm, ta thay các nghiệm vào hàm loss và so sánh các giá trị của chúng. Nghiệm cho giá trị nhỏ nhất chính là nghiệm cho cực tiểu trên toàn hàm loss mà ta cần tìm.

Nếu phương trình phức tạp hơn, chẳng hạn model không phải là tuyến tính. Việc tìm nghiệm bằng phương pháp đạo hàm có thể sẽ không thể thực hiện được. Lúc này ta cần một phương pháp khác để tìm giá trị tham số $\textbf{w}$ (có thể không phải là nghiệm) nhưng tối ưu nhất có thể. Đó chính là Gradient descent với điều kiện hàm loss phải là hàm lồi.

Lưu ý: Ở bài này, tôi sẽ theo hướng sử dụng Gradient descent để bạn đọc làm quen với Gradient descent. Trong thực tế, Linear Regression được cài đặt bằng cách tính đạo hàm tìm nghiệm trực tiếp vì lý do hiệu năng.

Phương pháp Gradient descent đơn giản là tận dụng sức mạnh tính toán của máy tính để dò nghiệm. Tức là thử các giá trị $\mathbf{w}$ vào hàm loss cho tới khi nào hàm loss đạt được giá trị nhỏ mà ta mong muốn.

Điều đáng chú ý ở đây là, chiến thuật thử $\mathbf{w}$ như thế nào cho hợp lý, bời vì nếu không có chiến thuật hợp lý, ta có thể sẽ phải thử vô số lần mà không tìm ra giá trị tối ưu!

Chiến thuật giúp gradient descent hoạt động tốt đó là dự vào gradient. Giá trị của $\mathbf{w_{t+1}}$ tại lần thử t+1 sẽ dựa vào gradient của hàm loss tại lần thử trước đó t. Cụ thể như sau:

$$\mathbf{w_{t+1}} = \mathbf{w_t} - lr*\frac{\partial{\mathcal{L}}}{\partial{\mathbf{w}}}(\mathbf{w_t})$$

Trong đó lr là learning rate - tốc độ học, là hằng số tốc độ cập nhật $\mathbf{w}$ mà ta mong muốn. Chẳng hạn lr ta chọn là 0.01.

Để tính đạo hàm của hàm loss, ta viết lại hàm loss như sau:

$$\mathcal{L}(\mathbf{w}) = \frac{1}{2N}\sum_{i=1}^{N}(y_i - \bar{\mathbf{x_i}}\mathbf{w})^2 = \frac{1}{2}\|\mathbf{y} - \bar{\mathbf{X}}\mathbf{w}\|_2^2$$

Trong đó $\|v\|_2$ là 2-norm của vector $v$. $\|v\|_2^2$ chỉ là bình phương 2-norm(v).

Đạo hàm của hàm loss theo $\mathbf{w}$ được tính như sau:

$$\frac{\partial\mathcal{L}}{\partial\mathbf{w}} = \bar{\mathbf{X}}^{T}(\bar{\mathbf{X}}\mathbf{w} - \mathbf{y})$$

Như vậy, $\mathbf{w}$ sẽ được cập nhật như sau:

$$\mathbf{w_{t+1}} = \mathbf{w_t} - lr*\frac{\partial{\mathcal{L}}}{\partial{\mathbf{w}}}(\mathbf{w_t}) = \mathbf{w_t} - lr*\bar{\mathbf{X}}(\bar{\mathbf{X}}\mathbf{w_{t}} - \mathbf{y})$$

Đó chính là điểm mấu chốt để ta có thể cài đặt thuật toán Linear regression sử dụng Gradient descent hay tôi gọi là Gradient Descent Linear Regression.

Cài đặt Gradient descent linear regression.

Lưu ý: bạn đọc tham khảo full file notebook cài đặt tại đây!

Ta sẽ khai báo một class GDLinearRegression bao gồm các hàm cơ bản như sau:

class GDLinearRegression:
  def __init__(self, lr, step):
    '''
    Khởi tạo learning rate và số lượng step update weigh
    '''
      
  def fit(self, X, y):
    ''' 
    Train the model với đầu vào là tập train data X cùng nhãn Y
    X là ma trận MxN trong đó M là số lượng điểm dữ liệu, mỗi điểm dữ liệu có N chiều.
    Trường hợp dữ liệu 1 chiều thì X là vector cột Mx1
    '''
  
  def predict(self, X):
    '''
    Thực hiện dự đoán
    '''

  def print_weight(self):
    '''
    In weigt w đã học được
    '''

  def get_train_loss(self):
    '''
    Trả về train loss đã lưu trong quá trình train
    '''

Hàm quan trọng nhất là hàm fit(), nơi ta tiến hành cập nhật $\mathbf{w}$ theo công thức toán học mà ta đã phân tích ở trên. Về cơ bản, hàm fit() sẽ phải có đoạn như sau:

def fit(self, X, y):

  # code tiền xử lý, khởi tạo
  ... 

  # vòng lặp train 
  for i in range(self.step):
      
    # tính đạo hàm tại điểm w_t
    delta = np.dot(X.T, ( np.dot(X, self.weight) - y))

    # update weight w_{t+1}
    self.weight = self.weight - (self.lr/train_size) * delta

Code đầy đủ của class GDLinearRegression sẽ như sau:

class GDLinearRegression:
  def __init__(self, lr, step):
    '''
    Khởi tạo learning rate và số lượng step update weigh
    '''
    self.lr = lr
    self.step = step
      
  def fit(self, X, y):
    ''' 
    Train the model với đầu vào là tập train data X cùng nhãn Y
    X là ma trận MxN trong đó M là số lượng điểm dữ liệu, mỗi điểm dữ liệu có N chiều.
    Trường hợp dữ liệu 1 chiều thì X là vector cột Mx1
    '''
    # lấy ra số lượng điểm train_size và số chiều dữ liệu n_features
    self.n_features = X.shape[1] if len(X.shape) > 1 else 1 
    train_size = len(X) # số lượng sample
    
    # chuẩn hóa lại định dạng dữ liệu
    X = X.reshape(-1, self.n_features)
    y = y.reshape([-1, 1])
    
    # ta muốn thực hiện dự đoán y = X.T*W + bias, ta đưa bias vào W (W|bias) và 1 cột toàn 1 vào X (X|one),
    # lúc đó việc tính toán thuận tiện hơn y = (X|one).T*(W|bias) => đây là trick để tính toán cho nhanh
    one = np.ones([train_size, 1])
    X = np.concatenate([X, one], 1)
    
    # tạo weight chính là parameters ta sẽ optimize trong quá trình train
    self.weight = np.zeros([self.n_features + 1, 1])
    print('x shape: ', X.shape, '- y shape: ', y.shape, '- weight shape: ', self.weight.shape, 'train_size: ', train_size)
    
    # mảng lưu lại toàn bộ giá trị loss trong quá trình train
    self.train_loss = []
    
    # train
    for i in range(self.step):
        
      loss = np.sum((y - np.dot(X, self.weight)) ** 2)
      delta = np.dot(X.T, ( np.dot(X, self.weight) - y))
      
      # update weight
      self.weight = self.weight - (self.lr/train_size) * delta
      
      # tính trung bình loss
      loss = loss/train_size
      self.train_loss.append(loss.item())
  
  def predict(self, X):
    '''
    Thực hiện dự đoán
    '''
    # chuẩn hóa format dữ liệu như ta đã làm trong lúc train
    X = X.reshape(-1, self.n_features)
    
    # thêm cột one như ta đã làm trong lúc train
    one = np.ones([len(X), 1])
    X = np.concatenate([X, one], 1)
    
    # thực hiện dự đoán, đơn giản là nhân ma trận
    y_hat = np.dot(X, self.weight)
    
    return y_hat
  
  def print_weight(self):
    '''
    In weigt đã học được
    '''
    print(self.weight)
      
  def get_train_loss(self):
    '''
    Trả về train loss đã lưu trong quá trình train
    '''
    return self.train_loss

Chúng ta thử áp dụng model GDLinearRegression đã cài đặt với 2 ví dụ ban đầu.

Áp dụng 1: dự đoán hàm số $y=-3x+5$

Tạo model với learning rate 0.1 và số lần lặp step là 1000:

model = GDLinearRegression(lr = 0.1, step = 1000) 

Thực hiện train model bằng hàm fit() và vẽ ra giá trị loss trong quá trình train:

model.fit(X_test, y_test)

train_loss = model.get_train_loss()
plt.plot(range(len(train_loss)), train_loss, 'r')
plt.title("training loss")
plt.xlabel("Step")
plt.ylabel("epoch")
plt.show()
print("last loss: ", train_loss[-1])

Nhận xét: giá trị loss giảm dần đến tiệp cận 0. Lúc này model đạt được một độ chính xác nhất định và không học thêm gì được nữa, ta có thể coi model đã converge tại gần điểm tối ưu.

Vẽ đồ thị thể hiện dự đoán trên tập test so với thực tế:

y_hat = model.predict(X_test)

plt.scatter(X_test, y_test)
plt.plot(X_test, y_hat, 'r')
plt.show()

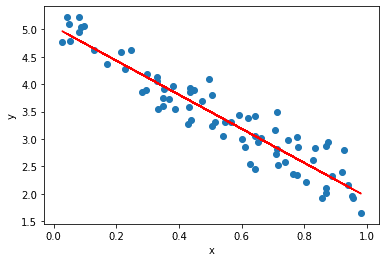
# kiểm tra lại weight đã học được, khá gần với hệ số trong hàm số y = -3x + 5
model.print_weight()

Giá trị weight học được bằng model của ta là $-3.10999554, 5.05090582$, trong khi hàm số $y=-3x+5$ có tham số là $-3, 5$. Dự đoán của ta đã khá gần với nghiệm đúng.

Áp dụng 2: dự đoán giá nhà Boston

Tạo model và train với tập train đã chia ở trên

# Ta đã thực hiện implement GDLinearRegression ở trên
# Giờ ta chỉ việc tạo mới model với learning rate là 0.01 và 
# số lượng step là 1000
mymodel = GDLinearRegression(0.01, 1000)
# thực hiện train dữ liệu
mymodel.fit(X_train, y_train)

# vẽ biểu đồi training loss
train_loss = mymodel.get_train_loss()
plt.plot(range(len(train_loss)), train_loss)
plt.xlabel('Step')
plt.ylabel('Loss')
plt.show()

Thực hiện dự đoán trên tập test

# thực hiện dự đoán trên tập test
y_hat = mymodel.predict(X_test)
mse = mean_squared_error(y_hat, y_test)

# in mean squared error trên tập test
print('Test MSE: ', mse)

Xem trực quan dự đoán của model trên tập test bằng đồ thị

# hiển thị đồ thị dữ liệu test (xanh) và đường dự đoán đã học được (đỏ)
plt.scatter(scalerx.inverse_transform(X_test), scalery.inverse_transform(y_test)) 
plt.plot(scalerx.inverse_transform(X_test), scalery.inverse_transform(y_hat), 'r')
plt.xlabel('House feature: RM')
plt.ylabel('Price')
plt.show()

Xem weight đã học được như thế nào:

# in weight học được w1, w0. 
mymodel.print_weight()

Kết quả: $0.7190214, 0.00251468$, nhận xét: Khá sát với weight học được bằng cộng cụ sklearn

Tổng kết

Ta đã làm quen với bài toán Linear regression để tạo model mô hình hóa dữ liệu có tính chất linear. Ta cũng làm quen với phương pháp Gradient descent để tìm tập tham số $\mathbf{w}$ tối ưu cho model, ta cũng đã tự tay viết code tạo model Linear regression từ nền tảng toán phía sau nó, và ta cũng đã train, test model với các tập dữ liệu cơ bản.

Phương pháp Gradient descent cũng có những ưu nhược điểm của nó, ở bài sau, ta sẽ phân tích kỹ hơn. Ngoài ra, ở bài sau, ta sẽ tìm hiểu các model phổ biến tiếp theo của Machine Learning. Mời các bạn đón đọc cũng như đóng góp ý kiến bổ sung cho bài viết này.