Linear Regression - Hồi quy tuyến tính trong Machine Learning

Trong bài viết, mình sẽ giới thiệu một trong những thuật toán cơ bản nhất của Machine Learning. Đây là thuật toán Linear Regression (Hồi Quy Tuyến Tính) thuộc nhóm Supervised learning ( Học có giám sát ). Hồi quy tuyến tính là một phương pháp rất đơn giản nhưng đã được chứng minh được tính hữu ích cho một số lượng lớn các tình huống. Trong bài viết này, bạn sẽ khám phá ra chính xác cách thức tuyến tính làm việc như thế nào. Trong việc phân tích dữ liệu, bạn sẽ tiếp xúc với thuật ngữ "Regression" ( Hồi quy ) rất thường xuyên. Trước khi đi sâu vào Hồi quy tuyến tính, hãy tìm hiểu khái niệm Hồi quy trước đã. Hồi quy chính là một phương pháp thống kê để thiết lập mối quan hệ giữa một biến phụ thuộc và một nhóm tập hợp các biến độc lập. Ví dụ :

Tuổi = 5 + Chiều cao * 10 + Trọng lượng * 13

Ở đây chính ta đang thiết lập mối quan hệ giữa Chiều cao & Trọng lượng của một người với Tuổi của anh/cô ta. Đây là một ví dụ rất cơ bản của Hồi quy.

Hồi quy tuyến tính giản đơn

Introduction

"Hồi quy tuyến tính" là một phương pháp thống kê để hồi quy dữ liệu với biến phụ thuộc có giá trị liên tục trong khi các biến độc lập có thể có một trong hai giá trị liên tục hoặc là giá trị phân loại. Nói cách khác "Hồi quy tuyến tính" là một phương pháp để dự đoán biến phụ thuộc (Y) dựa trên giá trị của biến độc lập (X). Nó có thể được sử dụng cho các trường hợp chúng ta muốn dự đoán một số lượng liên tục. Ví dụ, dự đoán giao thông ở một cửa hàng bán lẻ, dự đoán thời gian người dùng dừng lại một trang nào đó hoặc số trang đã truy cập vào một website nào đó v.v...

Chuẩn bị

Để bắt đầu với Hồi quy tuyến tính, chúng ta hãy đi lướt qua một số khái niệm toán học về thống kê.

• Tương quan (r) - Giải thích mối quan hệ giữa hai biến, giá trị có thể chạy từ -1 đến +1
• Phương sai (σ2) - Đánh giá độ phân tán trong dữ liệu của bạn
• Độ lệch chuẩn (σ) - Đánh giá độ phân tán trong dữ liệu của bạn (căn bậc hai của phương sai)
• Phân phối chuẩn
• Sai số (lỗi) - {giá trị thực tế - giá trị dự đoán}

Giả định

Không một kích thước nào phù hợp cho tất cả, điều này cũng đúng đối với Hồi quy tuyến tính. Để thoả mãn hồi quy tuyến tính, dữ liệu nên thoả mãn một vài giả định quan trọng. Nếu dữ liệu của bạn không làm theo các giả định, kết quả của bạn có thể sai cũng như gây hiểu nhầm.

1. Tuyến tính & Thêm vào : Nên có một mối quan hệ tuyến tính giữa biến độc lập và biến không độc lập và ảnh hưởng của sự thay đổi trong giá trị của các biến độc lập nên ảnh hưởng thêm vào tới các biến phụ thuộc.
2. Tính bình thường của phân bổ các lỗi : Sự phân bổ sai khác giữa các giá trị thực và giá trị dự đoán (sai số) nên được phân bổ một cách bình thường.
3. Sự tương đồng: Phương sai của các lỗi nên là một giá trị không đổi so với ,

• Thời gian
• Dự đoán
• Giá trị của các biến độc lập

4. Sự độc lập về thống kê của các lỗi: Các sai số (dư) không nên có bất kỳ mối tương quan nào giữa chúng. Ví dụ: Trong trường hợp dữ liệu theo chuỗi thời gian, không nên có sự tương quan giữa các sai số liên tiếp nhau.

Đường hồi quy tuyến tính

Trong khi sử dụng hồi quy tuyến tính, mục tiêu của chúng ta là để làm sao một đường thẳng có thể tạo được sự phân bố gần nhất với hầu hết các điểm. Do đó làm giảm khoảng cách (sai số) của các điểm dữ liệu cho đến đường đó.

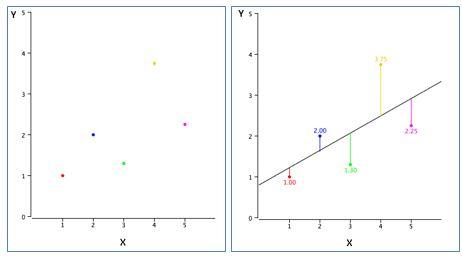
Ví dụ, ở các điểm ở hình trên (trái) biểu diễn các điểm dữ liệu khác nhau và đường thẳng (bên phải) đại diện cho một đường gần đúng có thể giải thích mối quan hệ giữa các trục x & y. Thông qua, hồi quy tuyến tính chúng ta cố gắng tìm ra một đường như vậy. Ví dụ, nếu chúng ta có một biến phụ thuộc Y và một biến độc lập X - mối quan hệ giữa X và Y có thể được biểu diễn dưới dạng phương trình sau:

Y = Β0 + Β1*X

Ở đây,

• Y = Biến phụ thuộc
• X = biến độc lập
• Β0 = Hằng số
• Β1 = Hệ số mối quan hệ giữa X và Y

Một vài tính chất của hồi quy tuyến tính

• Đường hồi quy luôn luôn đi qua trung bình của biến độc lập (x) cũng như trung bình của biến phụ thuộc (y)
• Đường hồi qui tối thiểu hóa tổng của "Diện tích các sai số". Đó là lý do tại sao phương pháp hồi quy tuyến tính được gọi là "Ordinary Least Square (OLS)"
• Β1 giải thích sự thay đổi trong Y với sự thay đổi X bằng một đơn vị. Nói cách khác, nếu chúng ta tăng giá trị của X bởi một đơn vị thì nó sẽ là sự thay đổi giá trị của Y

Tìm đường hồi quy tuyến tính

Sử dụng công cụ thống kê ví dụ như Excel, R, SAS ... bạn sẽ trực tiếp tìm hằng số (B0 và B1) như là kết quả của hàm hồi quy tuyến tính. Như lý thuyết ở trên, nó hoạt động trên khái niệm OLS và cố gắng giảm bớt diện tích sai số, các công cụ này sử dụng các gói phần mềm tính các hằng số này.

Ví dụ, giả sử chúng ta muốn dự đoán y từ x trong bảng sau và giả sử rằng phương trình hồi quy của chúng ta sẽ giống như y = B0 + B1 * x

x	y	Predict 'y'
1	2	Β0+B1*1
2	1	Β0+B1*2
3	3	Β0+B1*3
4	6	Β0+B1*4
5	9	Β0+B1*5
6	11	Β0+B1*6
7	13	Β0+B1*7
8	15	Β0+B1*8
9	17	Β0+B1*9
10	20	Β0+B1*10

Ở đây,

Độ lệch chuẩn x	3.02765
Độ lệch chuẩn y	6.617317
Trung bình x	5.5
Trung bình y	9.7
Tương quan x và y	.989938

Nếu chúng ta phân biệt các Tổng còn lại của diện tích sai số (RSS) tương ứng với B0 & B1 và tương đương với các kết quả bằng không, chúng ta có được các phương trình sau đây như là một kết quả:

B1 = Tương quan * ( Độ lệch chuẩn của y / Độ lệch chuẩn của x)
B0 = trung bình (Y) - B1 * Trung bình (X)

Đưa giá trị từ bảng 1 vào các phương trình trên,

B1 = 2,64
B0 = -2,2

Do đó, phương trình hồi quy nhất sẽ trở thành -

Y = -2,2 + 2,64 * x

Hãy xem, dự đoán của chúng ta như thế nào bằng cách sử dụng phương trình này

x	Y -giá trị thực	Y - Dự đoán
1	2	0.44
2	1	3.08
3	3	5.72
4	6	8.36
5	9	11
6	11	13.64
7	13	16.28
8	15	18.92
9	17	21.56
10	20	24.2

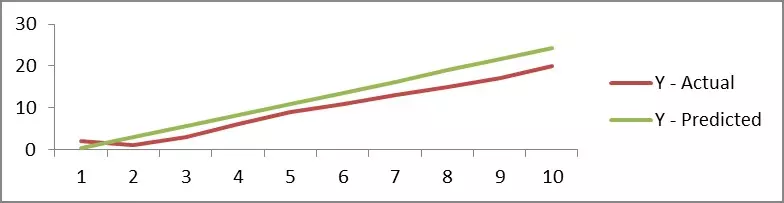
Chỉ với 10 điểm dữ liệu để phù hợp với một đường thẳng thì dự đoán của chúng ta sẽ chính xác lắm, nhưng nếu chúng ta thấy sự tương quan giữa 'Y-Thưc tế' và 'Y - Dự đoán' thì triển vọng sẽ rất cao do đó cả hai series đang di chuyển cùng nhau và đây là biểu đồ để hiển thị giá trị dự đoán:

Hiệu suất của mô hình

Một khi bạn xây dựng mô hình, câu hỏi tiếp theo đến trong đầu là để biết liệu mô hình của bạn có đủ để dự đoán trong tương lai hoặc là mối quan hệ mà bạn đã xây dựng giữa các biến phụ thuộc và độc lập là đủ hay không.

Vì mục đích này có nhiều chỉ số mà chúng ta cần tham khảo

R – Square (R^2)

Công thức tính R^2 sẽ bằng :

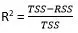
• Tổng các diện tích (TSS): TSS là một phép đo tổng biến thiên trong tỷ lệ đáp ứng / biến phụ thuộc Y và có thể được coi là số lượng biến thiên vốn có trong đáp ứng trước khi hồi quy được thực hiện.
• Sum of Squares (RSS): RSS đo lường lượng biến đổi còn lại không giải thích được sau khi thực hiện hồi quy.
• (TSS - RSS) đo lường mức độ thay đổi trong đáp ứng được giải thích (hoặc loại bỏ) bằng cách thực hiện hồi quy

Trong đó N là số quan sát được sử dụng để phù hợp với mô hình, σx là độ lệch chuẩn của x, và σy là độ lệch chuẩn của y.

• R2 giao động từ 0 đến 1.
• R2 của 0 nghĩa là biến phụ thuộc không thể dự đoán được từ biến độc lập
• R2 của 1 có nghĩa là biến phụ thuộc có thể được dự đoán mà không có sai số từ biến độc lập
• Một R2 giữa 0 và 1 chỉ ra mức độ mà biến phụ thuộc có thể dự đoán được. Một R2 của 0.20 có nghĩa là 20 phần trăm của phương sai trong Y có thể dự đoán được từ X; Một R2 của 0.40 có nghĩa là 40 phần trăm là có thể dự đoán v.v...

Root Mean Square Error (RMSE) RMSE cho biết mức độ phân tán các giá trị dự đoán từ các giá trị thực tế. Công thức tính RMSE là

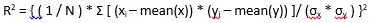
N: Tổng số quan sát

Mặc dù RMSE là một đánh giá tốt cho các sai số nhưng vấn đề với nó là nó rất dễ bị ảnh hưởng bởi phạm vi của biến phụ thuộc của bạn. Nếu biến phụ thuộc của bạn có dải biến thiên hẹp, RMSE của bạn sẽ thấp và nếu biến phụ thuộc có phạm vi rộng RMSE sẽ cao. Do đó, RMSE là một số liệu tốt để so sánh giữa các lần lặp lại khác nhau của mô hình

Mean Absolute Percentage Error (MAPE)

Để khắc phục những hạn chế của RMSE, các nhà phân tích thích sử dụng MAPE so với RMSE. MAPE cho sai số trong tỷ lệ phần trăm và do đó so sánh được giữa các mô hình. Công thức tính MAPE có thể được viết như sau:

N: Tổng số quan sát

Hồi quy tuyến tính đa biến

Cho đến hiện tại, chúng ta đã thảo luận về kịch bản mà chúng ta chỉ có một biến độc lập. Nếu chúng ta có nhiều hơn một biến độc lập, phương pháp phù hợp nhất là "Multiple Regression Linear" - Hồi quy tuyến tính đa biến

Sự khác biệt

Về cơ bản không có sự khác biệt giữa hồi quy tuyến tính 'giản đơn' và 'đa biến'. Cả hai đều làm việc tuân theo nguyên tắc OLS và thuật toán để có được đường hồi quy tối ưu nhất cũng tương tự. Trong trường hợp sau, phương trình hồi quy sẽ có một hình dạng như sau:

Y=B0+B1*X1+B2*X2+B3*X3.....

Ở đây,

Bi: Các hệ số khác nhau Xi: Các biến độc lập khác nhau

Chạy hồi quy tuyến tính bằng Python scikit-Learn

Ở trên, bạn đã biết rằng hồi quy tuyến tính là một kỹ thuật phổ biến và bạn cũng có thể thấy các phương trình toán học của hồi quy tuyến tính. Nhưng bạn có biết làm thế nào để thực hiện một hồi quy tuyến tính trong Python ?? Có một số cách để có thể làm điều đó, bạn có thể thực hiện hồi quy tuyến tính bằng cách sử dụng các mô hình thống kê, numpy, scipy và sckit learn. Nhưng trong bài này chúng ta sẽ sử dụng sckit learn để thực hiện hồi quy tuyến tính.

Scikit-learn là một module Python mạnh mẽ cho việc học máy. Nó chứa hàm cho hồi quy, phân loại, phân cụm, lựa chọn mô hình và giảm kích chiều. Chúng ta sẽ khám phá module sklearn.linear_model có chứa "các method để thực hiện hồi quy, trong đó giá trị mục tiêu sẽ là sự kết hợp tuyến tính của các biến đầu vào".

Trong bài đăng này, chúng ta sẽ sử dụng bộ dữ liệu Nhà ở Boston, bộ dữ liệu chứa thông tin về giá trị nhà cửa ở ngoại ô thành phố Boston. Tập dữ liệu này ban đầu được lấy từ thư viện StatLib được duy trì tại Đại học Carnegie Mellon và bây giờ đã có trên UCI Machine Learning Repository.

Khám phá bộ dữ liệu nhà Boston

Bộ Dữ liệu Nhà ở Boston bao gồm giá nhà ở những nơi khác nhau ở Boston. Cùng với giá cả, tập dữ liệu cũng cung cấp thông tin như Tội phạm (CRIM), các khu vực kinh doanh không-bán-lẻ ở thị trấn (INDUS), tuổi chủ sở hữu ngôi nhà (AGE) và có nhiều thuộc tính khác có sẵn ở đây . Bộ dữ liệu chính nó có thể down từ đây . Tuy nhiên, vì chúng ta sử dụng scikit-learn, chúng ta có thể import nó từ scikit-learn.

%matplotlib inline 

import numpy as np
import pandas as pd
import scipy.stats as stats
import matplotlib.pyplot as plt
import sklearn
import statsmodels.api as sm

import seaborn as sns
sns.set_style("whitegrid")
sns.set_context("poster")

# special matplotlib argument for improved plots
from matplotlib import rcParams

Trước hết, chúng ta sẽ import bộ dữ liệu Boston Housing và lưu trữ nó trong một biến gọi là boston. Để import nó từ scikit-learn, chúng ta sẽ cần phải chạy đoạn mã này.

from sklearn.datasets import load_boston
boston = load_boston()

Biến boston là một dạng từ điển, vì vậy chúng ta có thể kiểm tra key của nó sử dụng đoạn mã bên dưới.

print(boston.keys())

Nó sẽ trả về như sau

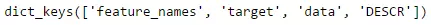
Tiếp,

print(boston.data.shape)

Trước tiên, chúng ta có thể dễ dàng kiểm tra shape của nó bằng cách gọi boston.data.shape và nó sẽ trả lại kích thước của tập dữ liệu với kích thước column.

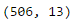
Như chúng ta có thể thấy nó trả về (506, 13), có nghĩa là có 506 hàng dữ liệu với 13 cột. Bây giờ chúng ta muốn biết 13 cột là gì. Chúng ta sẽ chạy đoạn code sau :

print(boston.feature_names)

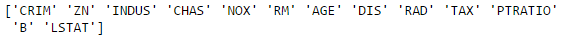
Bạn có thể dùng lệnh print(boston.DESCR) để kiểm tra description của dữ liệu thay vì mở web để đọc.

Tiếp, convert dữ liệu về dạng pandas! Rất đơn giản, gọi hàm pd.DataFrame() và truyền boston.data. Chúng ta có thể kiểm tra 5 dữ liệu đầu tiên bằng bos.head().

bos = pd.DataFrame(boston.data)
print(bos.head())

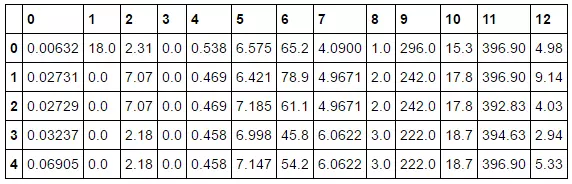
Hoặc bạn co thể dùng đoạn lệnh sau để show được tên cột

bos.columns = boston.feature_names
print(bos.head())

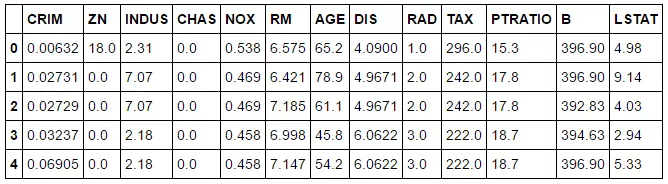
Có vẻ vẫn chưa có column tên là PRICE.

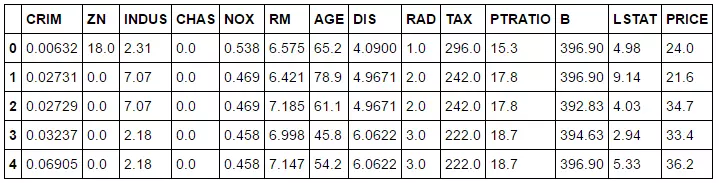
bos['PRICE'] = boston.target
print(bos.head())

Ta sẽ add nó vào sử dụng đoạn mã trên

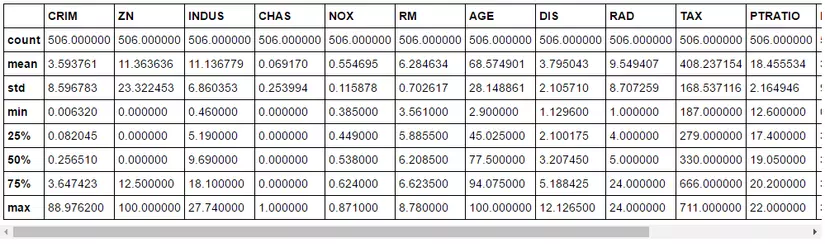
Nếu bạn muốn nhìn các số liệu tổng hợp thống kê, hãy chạy đoạn mã sau .

print(bos.describe())

Tách dữ liệu để train-test

Về cơ bản, trước khi chia dữ liệu thành tập dữ liệu để train - test, chúng ta cần chia dữ liệu thành hai giá trị : giá trị đích và giá trị dự báo. Hãy gọi giá trị đích Y và các giá trị dự báo X. Như vậy,

Y = Boston Housing Price
X = All other features

X = bos.drop('PRICE', axis = 1)
Y = bos['PRICE']

Bây giờ chúng ta có thể split dữ liệu để train và test với snippet như sau.

X_train, X_test, Y_train, Y_test = sklearn.cross_validation.train_test_split(X, Y, test_size = 0.33, random_state = 5)
print(X_train.shape)
print(X_test.shape)
print(Y_train.shape)
print(Y_test.shape)

Nếu chúng ta kiểm tra shape của mỗi biến, chúng ta đã có được bộ dữ liệu với tập dữ liệu thử nghiệm có tỷ lệ 66,66% đối với dữ liệu train và 33,33% đối với dữ liệu test.

Linear Regression

Tiếp, chúng ta sẽ chạy hồi quy tuyến tính.

from sklearn.linear_model import LinearRegression

lm = LinearRegression()
lm.fit(X_train, Y_train)

Y_pred = lm.predict(X_test)

plt.scatter(Y_test, Y_pred)
plt.xlabel("Prices: $Y_i$")
plt.ylabel("Predicted prices: $\hat{Y}_i$")
plt.title("Prices vs Predicted prices: $Y_i$ vs $\hat{Y}_i$")

Đoạn mã trên sẽ phù hợp với một mô hình dựa trên X_train và Y_train. Bây giờ chúng tôi đã có mô hình tuyến tính, chúng ta sẽ cố gắng dự đoán nó cho X_test và các giá trị dự đoán sẽ được lưu trong Y_pred. Để hình dung sự khác biệt giữa giá thực tế và giá trị dự đoán, chúng tôi cũng tạo ra một bảng biểu .

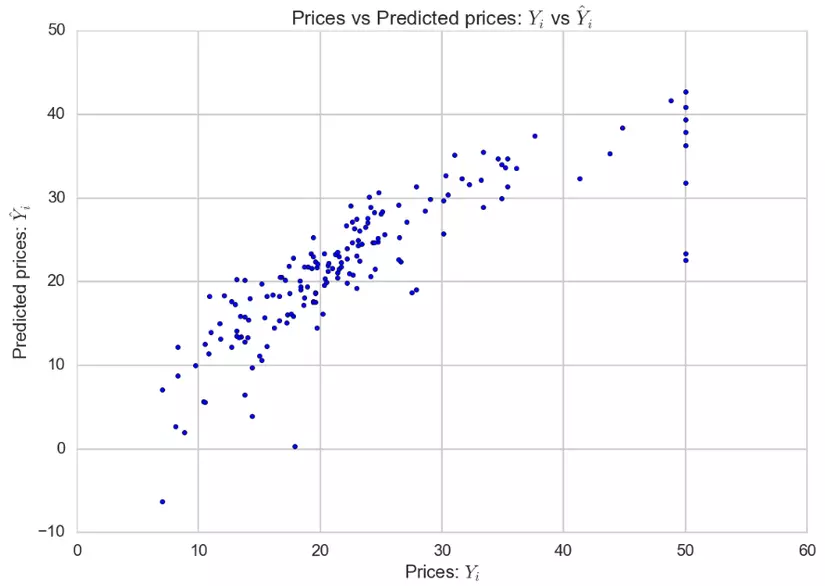
Thực tế thì đáng lẽ đồ thị ở trên phải tạo một đường tuyến tính như chúng ta đã thảo luận lý thuyết ở trên. Tuy nhiên, model không thích hợp 100%, cho nên nó đã ko thể tạo được đường tuyến tính.

Trung bình diện tích sai số

Để kiểm tra mức độ lỗi của một mô hình, chúng ta có thể sử dụng Mean Squared Error. Đây là một trong các phương pháp để đo trung bình của ô vuông của sai số. Về cơ bản, nó sẽ kiểm tra sự khác biệt giữa giá trị thực tế và giá trị dự đoán. Để sử dụng nó, chúng ta có thể sử dụng hàm bình phương trung bình sai số của scikit-learn bằng cách chạy đoạn mã này

mse = sklearn.metrics.mean_squared_error(Y_test, Y_pred)
print(mse)

kết quả nhận được

28.5413672756

Tham khảo và dịch

http://bigdata-madesimple.com/how-to-run-linear-regression-in-python-scikit-learn/

http://aimotion.blogspot.com/2011/10/machine-learning-with-python-linear.html

http://machinelearningmastery.com/simple-linear-regression-tutorial-for-machine-learning/

http://machinelearningmastery.com/implement-simple-linear-regression-scratch-python/

https://medium.com/@haydar_ai/learning-data-science-day-9-linear-regression-on-boston-housing-dataset-cd62a80775ef