Linear Regession with One Variable

Linear Regession (Hồi quy tuyến tính) là một trong những thuật toán Machine Learning cơ bản nhất. Đây là một thuật toán Supervised Learning, đôi khi nó còn được gọi là Linear Fitting hoặc Linear Least Square.

Model Representation

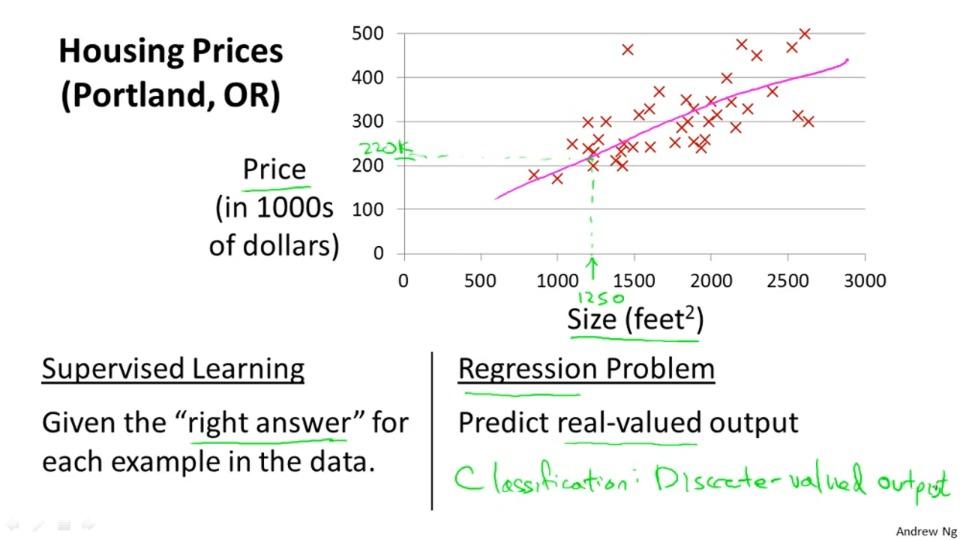
Trong bài này, chúng ta sẽ xét mô hình cơ bản của hồi quy tuyến tính. Cho một căn nhà với bộ dữ liệu training gồm có diện tích và giá trị của căn nhà đấy. Chúng ta sẽ cần dự đoán với một căn nhà có diện tích bất kì thì giá căn nhà đó sẽ là bao nhiêu.

Ở đây chúng ta sẽ có:

• $m=47$ là số lượng training example.
• $x$ là dữ liệu đầu vào hay đặc điểm, tính chất của căn nhà.
• $y$ là dữ liệu đầu ra hay đặc điểm tính chất mà ta cần (giá trị căn nhà).

Để thống nhất ký hiệu về sau, chúng ta sử dụng $x^{(i)}$ là biến nhập vào (diện tích căn nhà trong ví dụ này), $y^{(i)}$ là biến output (giá trị căn nhà). Với mỗi cặp $(x^{(i)},y^{(i)})$ là một cặp "training example". Lượng dữ liệu data chúng ta dùng để train là một list $m$ training examples. $(x^{(i)},y^{(i)}); i = 1,2,...m$ là một training set. $X$ là không gian vecto $x$ trong ví dụ này, $Y$ là không gian vecto output. Trong ví dụ này $X=Y=\mathbb{R}$

Để thể hiện rõ Supervised Learning, mục tiêu chúng ta là khi được cho bộ training set, tạo một hàm $h: X \rightarrow Y$ để dự đoán giá trị của $y$. Thuật toán được thể hiện như sau:

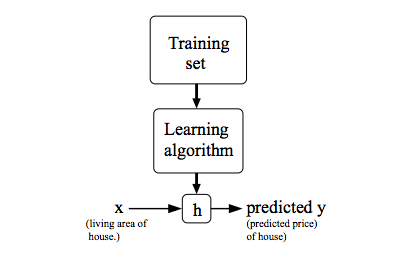
Khi đầu ra $y$ là một giá trị liên tục, như diện tích ngôi nhà, chúng ta gọi bài toán đó là hồi quy. Khi đầu ra $y$ chỉ nhận một vài giá trị rời rạc (ví dụ khi được cho diện tích một căn nhà hoặc căn hộ chung cư, ta sẽ cần dự đoán xem là nhà riêng hay chung cư) được gọi là bài toán phân loại.

Cost Function

Cost Function hay còn được gọi là Loss Function, là hàm chi phí của hàm $h(x)$. Hàm $h(x)$ là một hàm tuyến tính theo $x$, dùng để dự đoán giá trị đầu ra $y$: $h(x)=\theta_{0}+\theta_{1}x$.

Giá trị dự đoán sẽ có thể có sai số, ta biểu diễn: $\hat{y} = h(x) \approx y$ . Ở đây, $y$ là giá trị thực, $\hat{y}$ là giá trị dự đoán.

Mục tiêu của ta là tìm $\theta_{0},\theta_{1}$ sao cho tổng giá trị $h(x_{i})-y_{i}$ với $i=1,...,m$ là gần $0$ nhất. Ta sẽ có hàm chi phí $J(\theta_{1},\theta_{2})$ như sau:

$\displaystyle J(\theta_{1},\theta_{2})=\frac{1}{2m}\sum_{i=1}^m(h(x_{i})-y_{i})^2$

• Câu hỏi thứ nhất là tại sao lại là $(h(x_{i})-y_{i})^2$ mà không phải $\left | h(x_{i})-y_{i} \right |$. Lý do là hàm trị tuyệt đối thì không có đạo hàm ở $0$

• Câu hỏi thứ hai là giá trị $\displaystyle\frac{1}{2}$ ở đâu ra? Giá trị $\displaystyle\frac{1}{2}$ là để thuận tiện cho việc tính toán, khi đạo hàm bình phương thì sẽ mất $\displaystyle\frac{1}{2}$

Gradient Descent

Giờ chúng ta đã có hàm ước tính $h$ và cách để đánh giá độ chính xác của nó với bộ data được nhận. Công việc tiếp theo là tìm các tham số trong hàm $h$ đó. Vì vậy, chúng ta cần đến Gradient Descent.

Mô hình chung

Tưởng tượng rằng chúng ta biểu diễn hàm cần tìm $h$ "based on its fields $\theta_{0}$ and $\theta_{1}$" (Đoạn này không biết diễn ta bằng tiếng việt như nào nôm na là dựa trên mặt phẳng tạo bởi $\theta_{0}$ và $\theta_{1}$ khi chúng chạy trên $\mathbb{R}$).

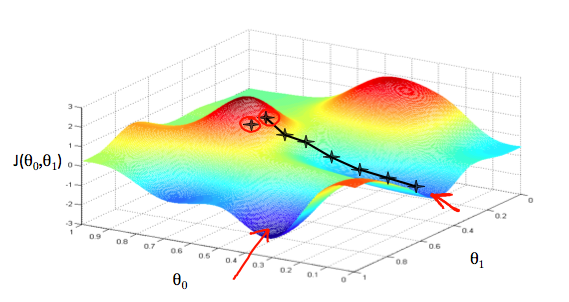
Chúng ta đạt được mục tiêu khi hàm chi phí đạt đến giá trị nhỏ nhất.

Cách thực hiện là đạo hàm hàm chi phí như ở toán cao cấp để tìm cực trị. Ở đây, chúng ta tiếp cận việc tìm nghiệm của đạo hàm theo một hướng mới. Thuật toán Gradient Descent sẽ như sau:

repeat until convergence:

$\theta_{j} := \theta_{j} - \alpha\frac{\partial{J(\theta_{0},\theta_{1})}}{\partial{\theta_{j}}}$ where $j=0$ and $j=1$

Với nhiều $\theta_{0}, \theta_{1}, \theta_{2} ...$ ta phải update đồng thời chúng. Trình tự đúng như sau:

với $\alpha$ là "Learning Rate". Learning Rate còn được gọi là Step Size, là một tham số để ta kiểm soát việc xác định giá trị tiếp theo của $\theta$. Hầu hết lập trình viên dành thời gian để tinh chỉnh Learning Rate. Nếu Learning Rate quá nhỏ, thuật toán sẽ tốn nhiều thời gian, nếu Learning Rate quá lớn, nó có thể sẽ bỏ qua điểm cực trị. Quan sát hình minh họa sau đây:

• Learning Rate quá nhỏ:

• Learning Rate quá lớn:

• Learning Rate hợp lý:

Tham khảo Machine Learning Crash Course

Với việc chọn Learning Rate hợp lý, ta sẽ dùng thuật toán để tìm được điểm cực tiểu:

Cụ thể hàm chi phí (Cost Function) của ví dụ trên

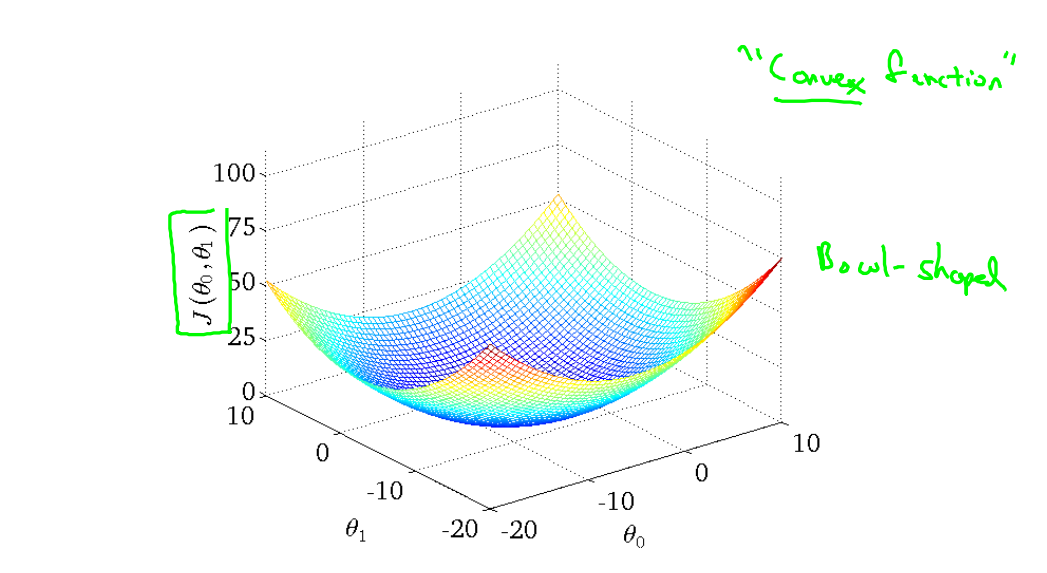
Nhìn vào hàm chi phí, ta thấy nó là tổng của các bình phương của một tổng nên không thể âm được, giá trị nhỏ nhất sẽ gần $0$ nhất.

$\frac{\partial{J(\theta_{0},\theta_{1})}}{\partial{\theta_{j}}}=\frac{\partial{J(\theta_{1},\theta_{2})}}{\partial{\theta_{j}}}=\frac{\partial{}}{\partial{\theta_{j}}}\frac{1}{2m}\sum_{i=1}^m(h(x_{i})-y_{i})^2=\frac{\partial{}}{\partial{\theta_{j}}}\frac{1}{2m}\sum_{i=1}^m(\theta_{0}+\theta_{1}x_{i}-y_{i})^2$

$\frac{\partial{J(\theta_{0},\theta_{1})}}{\partial{\theta_{1}}}=\frac{1}{m}\sum_{i=1}^m(\theta_{0}+\theta_{1}x_{i}-y_{i})$

$\frac{\partial{J(\theta_{0},\theta_{1})}}{\partial{\theta_{1}}}=\frac{1}{m}\sum_{i=1}^m(\theta_{0}+\theta_{1}x_{i}-y_{i})x_{i}$

Gradient Descent Algorithm

repeat until convergence:

$\theta_{0} := \theta_{0} - \alpha\frac{1}{m}\sum_{i=1}^m(\theta_{0}+\theta_{1}x_{i}-y_{i})$

$\theta_{0} := \theta_{0} - \alpha\frac{1}{m}\sum_{i=1}^m(\theta_{0}+\theta_{1}x_{i}-y_{i})x_{i}$

update $\theta{1}$ and $\theta{2}$ simultaneously

Sau khi tìm được $\theta{1}$ và $\theta{2}$ tối ưu, ta tìm được hàm $h(x)$ là một đường tuyến tính để dự đoán giá trị của $y$

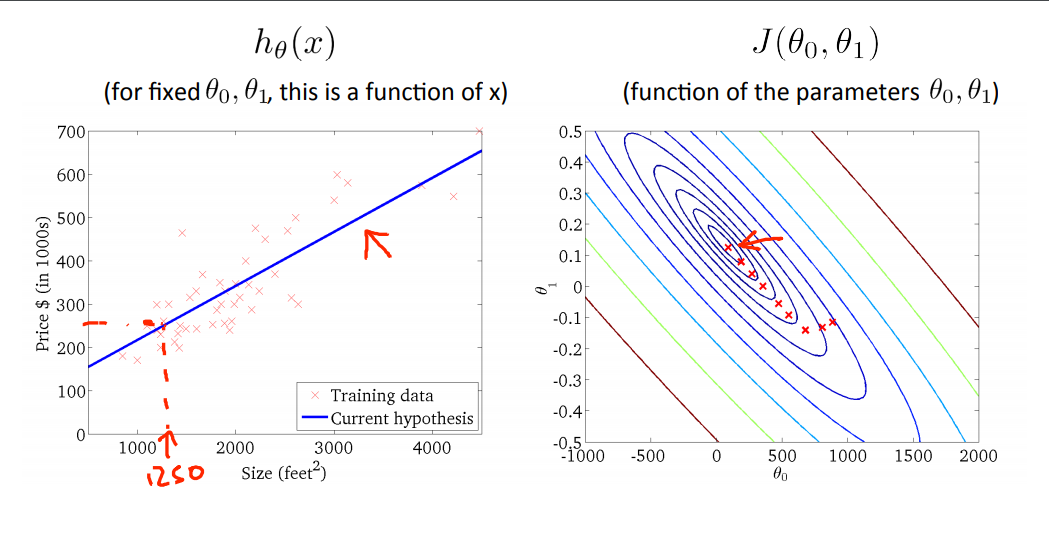
(còn tiếp)

Bài viết là quá trình ghi lại khi tham gia khóa học Machine Learning của thầy Andrew Ng và tham khảo tài liệu từ blog Machine Learning cơ bản.