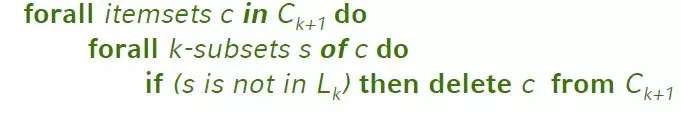1. Tổng quan:

Bài toán khai thác tập phổ biến (frequent itemset) là lớp bài toán rất quan trọng trong lĩnh vực khai phá dữ liệu. Mục tiêu của nó là tìm tất cả các tập mẫu, liên kết, tương quan hoặc cấu trúc nhân quả có độ phổ biến cao trong tập hợp tất cả các hạng mục hoặc đối tượng trong cơ sở dữ liệu giao dịch, cơ sở dữ liệu quan hệ và các kho thông tin dữ liệu khác.

Có bao giờ bạn tự hỏi tại sao các mặt hàng sản phẩm này trong siêu thị lại được xếp cạnh nhau?. Tại sao mặt hàng A lại được xếp ở dưới, mặt hàng B lại được xếp ở trên cao? Tại sao các món đồ ta cần thường được xếp cạnh nhau trong siêu thị nhỉ? Đây chính là một phần ứng dụng việc khai phá dữ liệu mà cụ thể hơn là khai phá các tập phổ biến!

Bài toán khai thác các tập phổ biến được ứng dụng trong rất nhiều vấn đè, nổi tiếng nhất là Basket data analysis (dự đoán, gợi ý các món hàng thường được cho cùng vào giỏ hàng với món đồ A đã được chọn mua trước đó). Ngoài ra nó còn được ứng dụng trong lớp các bài toán: tiếp thị chéo, thiết kế danh mục, phân tích thua lỗ, phân cụm, phân loại, hệ thống khuyến nghị, v.v. Và đặc biệt nó còn thể ứng dụng cho thiết kế các dịch vụ tiện ích trong nhà thông minh Ứng dụng làm một số task khá dị nhưng lại đem lại hiệu quả không ngờ . Cái này mình đang thực hiện và có thể sẽ giới thiệu cho các bạn trong các bài viết sau.

Bài toán sắp xếp các mặt hàng làm sao để tăng lợi nhuận:

Một số kí hiệu và định nghĩa sẽ được sử dụng:

1. Items I = {i1, i2, … , im}: Tập các hạng mục hay đối tượng của bài toán với ip ≠ iq với mọi p, q.

2. Itemset X: Tập các hạng mục X ⊆ I.

3. Cơ sở dữ liệu D: Tập hợp các giao dịch T, mỗi giao dịch là một tập danh sách các hạng mục T ⊆ I.

4. Giao dịch T chứa một itemset X: X ⊆ T.

5. Các hạng mục trong các giao dịch và các itemsets được sắp xếp theo một thứ tự nhất định:

   VD: itemset X = (x1, x2, …, xk) với x1 ≤ x1 ≤ … ≤ xk.

6. Độ dài của một itemset: Số lượng phần tử có trong itemset đó. k-itemset: itemset có độ dài là k.

7. Độ phổ biến hay hỗ trợ của một itemset X được định nghĩa là: support(X) = |{T ∈ D| X ⊆ T}|.

8. Các tập phổ biến: Một itemset X được gọi là phổ biến cho cơ sở dữ liệu D nếu tần suất xuất hiện trong các giao dịch T của giao dịch D thỏa mãn: support(X) ≥ minSup.

9. Độ tin cậy cậy: Cho hai tập phổ biến X và Y. Độ tin cậy của mệnh đề kéo theo X => Y là : confidence(X=>Y) = (support(X => Y))/(support(X)).

10. Các luật tin cậy: Một luật X => Y được công nhận nếu nó thỏa mãn confidence(X=>Y) ≥ minConf.

11. Trong đó minSup và minConf là các ngưỡng được định nghĩa từ trước.

2. Khai thác các tập phổ biến thông qua hai thuật toán Apriori và FP Growth:

2.1. Giới thiệu chung về hai thuật toán:

• Apriori và FP Growth là hai thuật toán rất nổi tiếng cho lớp bài toán này. Trong đó Apriori là một trong những thuật toán đầu tiên và là nền móng phát triển cho các thuật toán khai thác các tập phổ biến sau này. Mỗi thuật toán đều có những ưu và nhược điểm riêng. Tùy vào bản chất của bài toán, bộ dữ liệu được sử dụng mà dùng thuật toán này sẽ có lợi hơn thuật toán còn lại.

• Apriori được đề xuất lần đầu tiên bởi R. Agrawal và R. Srikant năm 1994. Hai chiến lược được sử dụng là xây dựng từ dưới lên và tìm kiếm theo chiều rộng. Ý tưởng chính của thuật toán này là sinh các tập ứng cử k-th candidate itemsets (các tập có khả năng là các tập phổ biến nếu thỏa mãn điều kiện minSup) từ các tập phổ biến (k-1)-th frequent itemsets trước đó. Rồi tìm các tập phổ biến k-th frequent itemsets từ các tập ứng cử k-th candidate itemsets mới được sinh ra. Thuật toán dừng lại khi các tập phổ biến frequent itemset không thể mở rộng lên được nữa. Nhược điểm của thuật toán Apriori là thời gian thực hiện rất lớn lãng phí nhiều thời gian ở quá trình sinh ra cá tập ứng cử viên candidate itemsets. Không gian tìm kiếm lớn và chi phí tính toán cũng rất cao. Hai nguyên tắc của Apriori giúp thuật toán hoạt động và giảm chi phí tính toán ở bước cắt tỉa (sẽ được nói đến ở phần sau):

  • Nếu một itemset là phổ biến thì tất cả các tập con của nó cũng phải là các tập phổ biến.

    => Là tư tưởng được sử dụng trong quá trình cắt tỉa.

  • Mọi tập cha của một itemset không phổ biến đều là các tập không phổ biến.

    => Là tư tưởng để xây dựng các tập phổ biến từ dưới lên trên.

• FP Growth khám phá các tập phổ biến frequent itemsets mà không cần sinh ra các tập ứng cử viên candidate itemsets. Thuật toán được thực hiện với hai bước chính: bước (1) Xây dựng một cấu trúc dữ liệu nhỏ gọn được gọi là cây FP-tree và bước (2) Trực tiếp trích xuất các tập phổ biến frequent itemsets từ cây FP-tree. FP-tree lần đầu tiên được đề bở Han. Ưu điểm của nó là xây dựng cơ sở dữ mẫu điều kiện từ cơ sở dữ liệu thỏa mãn độ hỡ trợ tối thiểu. Do cấu trúc cây nhỏ gọn và không tạo ra các tập ứng cử viên candidate itemsets nên yêu cầu ít bộ nhớ hơn. Nhược điểm của nó là hoạt động kém với các tập dữ liệu có mẫu dài (độ dài k của itemset lớn).

2.2. Thuật toán Apriori:

a. 3 bước để khai thác được các tập phổ biến:

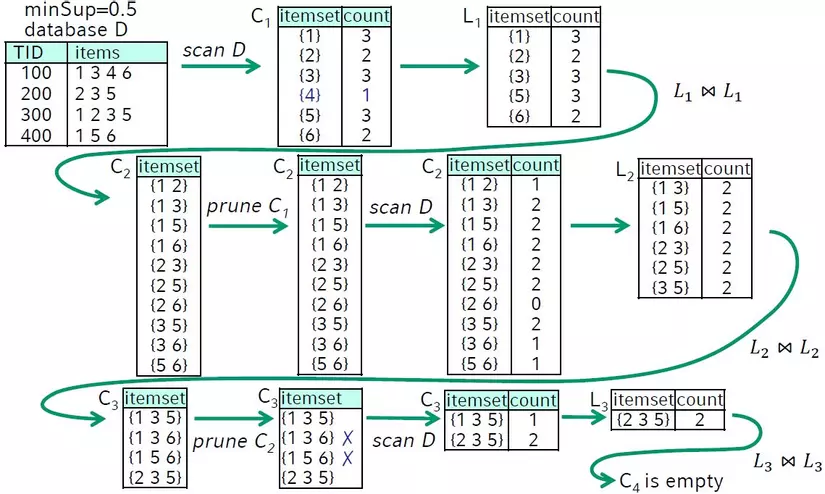
1. Bước khởi tạo và kiểm tra: Khởi tạo tập các ứng cử viên 1th-itemset C1 là tất cả các item có trong bài toán. Tìm các tập phổ biến 1-itemset L1 bằng cách quét cơ sở dữ liệu và xóa tất cả các phần tử không thỏa mãn độ hỗ trợ tối thiểu minSup khỏi C1.

2. Bước kết hợp - Join Step:

Tạo ra các tập ứng cử viên candidate itemset ở cấp độ tiếp theo:

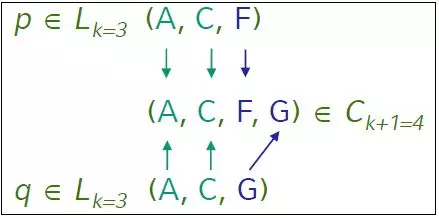
• Giả sử ta có 2 tập phổ biến trước đó là k-itemset p và q.
• p và q có thể kết hợp với nhau để tạo ra tập ứng cử viên k+1-itemset nếu chúng có chung k-1 item đầu tiên.

3. Bước cắt tỉa - Pruning

Ý tưởng ngây thơ: Kiểm tra hết tất cả độ phổ biến của mọi itemset ứng cử viên Ck+1 => Không hiệu quả với số lượng lớn các tập Ck+1 được sinh ra.

Giải pháp thay thế: Áp dụng nguyên tắc thứ nhất của giải thuật Apriori đã nêu ở trên: Loại bỏ tất cả các tập ứng cử viên (k+1) - itemsets mà chứa các tập không phổ biến k-subset:

• L3 = {(ACF), (ACG), (AFG), (AFH), (CFG)}
• Tập ứng cử viên sau bước kết hợp: {(ACFG), (AFGH)}
• Trong bước cắt xén: Xóa tập (AFGH) do có tập con là (FGH) không thuộc L3 ( tập phổ biến 3-itemset sinh ra ở bước trước đó); Tương tự với tập (AGH) không thuộc L3.
• C4 = {(ACFG)} có các tập con đều thỏa mãn nguyên tắc thứ nhất => Kiểm tra độ phổ biến để sinh ra L4.

Bước 2 và 3 sẽ được lặp đi lặp lại cho đến khi không thể sinh thêm các tập ứng viên được nữa.

b. Mã giả cho thuật toán Apriori

c. Ví dụ đầy đủ áp dụng thuật toán Apriori

Một chú ý nhỏ cho các bạn là các thuật toán trên chỉ áp dụng cho các cơ sở dữ liệu kiểu giao dịch. Tức là các item có hay không có xuất hiện trong một giao dịch (dạng 0,1). Do đó với các item có nhiều giá trị thì cần sử dụng các kĩ thuật nhờ rời rạc hóa, phân cụm, hay áp dụng các kĩ thuật trong logic mờ.... để có thể áp dụng được thuật toán khai thác tập phổ biến. Phần này có thể mình sẽ nói thêm trong một bài viết sau này .

Bài tiếp theo sẽ là về thuật toán FP-Growth và so sánh chi tiết các khía cạnh giữa hai thuât toán Apriori và FP-Growth giúp các bạn có thể hình dung được lúc nào thì cần dùng thuật toán nào để có thể đem lại hiệu quả nhất cho vấn đề ta đang giải quyết.

Đây là bài đầu tiên mình chia sẻ trên Viblo nên có thể còn nhiều sai sót. Mong các bạn ủng hộ và góp ý để mình có thể viết những bài chất lượng hơn.

Tài liệu tham khảo:

• KAVITHA, M.; SELVI, ST Tamil. Comparative Study on Apriori Algorithm and Fp Growth Algorithm with Pros and Cons. International Journal of Computer Science Trends and Technology (I JCS T)–Volume, 2016, 4.
• Ludwig-Maximilians-Universität München Institut für Informatik Lehrstuhl für Datenbanksysteme und Data Mining Oettingenstraße 67 80538 München, Germany: https://www.dbs.ifi.lmu.de/Lehre/KDD/SS16/skript/3_FrequentItemsetMining.pdf