Image clustering for reducing the number of colors

Bài đăng này đã không được cập nhật trong 3 năm

Introduction to clustering

The most common type of machine learning tasks are supervises learning. The training data consist of a set of training examples. In supervised learning, each example is a pair consisting of an input object (typically a vector) and a desired output value (also called the supervisory signal). A supervised learning algorithm analyzes the training data and produces an inferred function, which can be used for mapping new examples. An optimal scenario will allow for the algorithm to correctly determine the class labels for unseen instances. If there are only objects, and there are no answers for them, you can still try to find some structure in the data. Tasks that look for regularities in unmetered samples are called unsupervised tasks. A typical example of such a task is cluster analysis or clustering, where you want to find groups of similar objects. Clustering can be used for a variety of purposes. This article discusses the grouping of similar pixels in an image. This approach allows us to move to a super-pixel representation of images, which is more compact and better suited for solving a number of computer vision problems.

example of clustering application

Task. Group by similar pixels in the image.

The quality is estimated using the Peak signal-to-noise ratio Original image:

Instruments

Python and packages such as Pandas, Numpy, SciImage, and Scikit-Learn, which realizes many algorithms machine learning.

import pandas
import numpy as np
import math
from skimage.io import imread, imsave
from skimage import img_as_float
from sklearn.cluster import Kmeans

Solution with K-Means algorithm.

Load the image parrots.jpg and convert all the values in the interval from 0 to 1.

image = img_as_float(imread('parrots.jpg'))
w, h, d = image.shape   //  OUT: (474, 713, 3)

Create a matrix-signs objects: represent each pixel by three coordinates - values in RGB space intensity.

data = pandas.DataFrame(np.reshape(image, (w*h, d)), columns=['R', 'G', 'B'])

Start the K-Means algorithm with init = 'k-means ++' and random_state = 241. After allocation of clusters, all the pixels assigned to one cluster, try to fill in two ways: median and medium color on the cluster.

kmeans = KMeans(init='k-means++', random_state=241).fit(data)

def cluster(pixels, n_clusters=8):
    print('Clustering: ', n_clusters)

    pixels = pixels.copy()
    model = KMeans(n_clusters=n_clusters, init='k-means++', random_state=241)
    pixels['cluster'] = model.fit_predict(pixels)

    means = pixels.groupby('cluster').mean().values
    mean_pixels = [means[c] for c in pixels['cluster'].values]
    mean_image = np.reshape(mean_pixels, (w, h, d))
    imsave('mean/parrots_' + str(n_clusters) + '.jpg', mean_image)

    medians = pixels.groupby('cluster').median().values
    median_pixels = [medians[c] for c in pixels['cluster'].values]
    median_image = np.reshape(median_pixels, (w, h, d))
    imsave('medium/parrots_' + str(n_clusters) + '.jpg', median_image)

    return mean_image, median_image

Measure the quality of the resulting segmentation using the PSNR (peak-to-noise ratio) metric. It is an engineering term for the ratio between the maximum possible power of a signal and the power of corrupting noise that affects the fidelity of its representation. Because many signals have a very wide dynamic range, PSNR is usually expressed in terms of the logarithmic decibel scale. 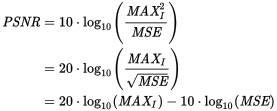PSNR here, MSE - mean square error MAXI is the maximum possible pixel value of the image

def psnr(image1, image2):
    mse = np.mean((image1 - image2) ** 2)
    return 10 * math.log10(float(1) / mse)

Find the minimum number of clusters at which the PSNR value is above 20 (Consider no more than 20 clusters).

for n in range(1, 21):
    mean_image, median_image = cluster(data, n)
    psnr_mean, psnr_median = psnr(image, mean_image), psnr(image, median_image)
    print(psnr_mean, psnr_median)

    if psnr_mean > 20 or psnr_median > 20:
        print(1, n)
        break