"Học máy" trong mô hình hồi quy tuyến tính, phân loại tuyến tính.
Bài đăng này đã không được cập nhật trong 6 năm
1.Đặt câu hỏi ?
Note: Bài này sẽ không bàn về cách để bạn có thể sử dụng một mô hình học máy cụ thể nào nhưng mình tin nó sẽ giúp ích cho bạn có một cái nhìn cơ bản nhất về Học máy thông qua một số ví dụ về mô hình hồi tuyến tính.
Một máy tính chỉ đọc được 2 loại tín hiệu 0 và 1 vậy chúng thực sự học như thế nào ?
2. Mô hình hồi quy tuyến tính
2.1 Tiền đề
Trước khi bắt tay vào tìm hiểu mô hình hồi quy tuyến tính mình sẽ bắt đầu so sánh giữa con người và máy.
Mọi quy trình xử lý cho dù của con người hay máy móc đều diễn ra theo một quy trình cơ bản sau đây:
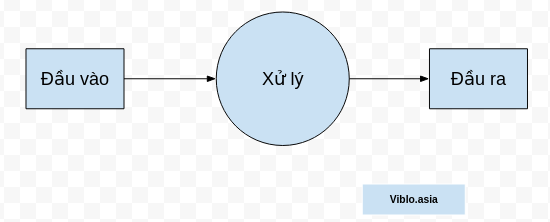
Nhưng nếu phân chia kỹ ra để lấy sự khác biệt giữa con người và máy, ta sẽ cần định nghĩa ra "Xử lý" một cách rõ ràng hơn. Và mình xin phép được viết ở dưới đây:
Như vậy đối với con người, mình sẽ dùng từ "Suy nghĩ".
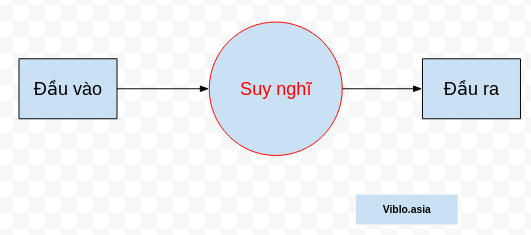
Và với máy tính, bên trong xử lý của máy tính chỉ là những phép tính toán, nên xử lý ở đây chỉ có thể hiểu là "Tính toán" không hơn không kém.
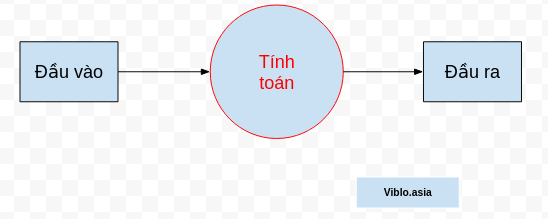
2.2 Quay lại với mô hình
Như vậy phần Tiền đề mình nói ở trên có liên quan gì đến mô hình hồi quy tuyến tính, mình xin được giải thích dần dần ở dưới đây.
Mình sẽ lấy ra một ví dụ về mô hình tính toán của máy tính như sau:
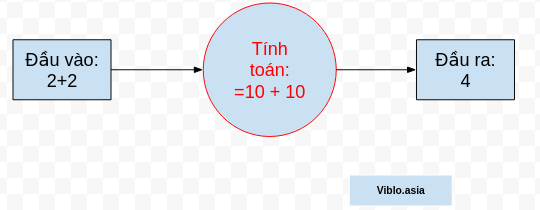
Đầu tiên ta cho dữ liệu đầu vào là một phép tính và mong muốn máy tính sẽ chuyển về hệ nhị phân để tính toán và cho ra một đầu ra là một kết quả của phép tính đó. Cho đến thời điểm hiện tại, cái cốt lõi của mày tính chúng ta cũng chỉ làm được như vậy, không hơn không kém. Và nó làm công việc này rất nhanh đến nỗi mà không một nhà bác học nào có thể bằng được.
Vậy mình sẽ tạo một mô hình dự đoán đơn giản mang tính chất "học máy" một chút. Mình sẽ chọn mô hình chuyển đổi từ đơn vị đo km ( ki-lô-mét) sang m (mét). Chúng ta ai cũng biết rằng 1km = 1000m nhưng lần này mình sẽ giả sử rằng máy của mình không biết cái hệ số này và mình sẽ cho nó học từ 1 tập dữ liệu để nó có thể tự tìm ra hệ số này cho mình.
Ở bài bên trên mình có một công thức như sau:
met = kilomet * c
Trong đó c ở đây là một hằng số mà chúng ta cần tìm. Và chúng ta sẽ giúp cho máy của chúng ta có thể tự tìm ra hằng số đó thông qua việc train model. Và công việc của train model sẽ diễn ra như quy trình dưới đây.
- Đầu tiên chúng ta cần dữ liệu Mình có 1 bảng dữ liệu sau đây và cùng xem máy sẽ học thế nào nhé.
| STT | kilomet | met |
|---|---|---|
| 1 | 3 | 3000 |
| 2 | 2 | 2000 |
Chúng ta đã có công thứcmet = km*c rồi, thông qua bảng trên chúng ta đã có kilomet và met, công việc của chúng ta chính là giúp máy tìm ra được hằng số c.
Vậy hãy thử random 1 hằng số c nào đó thử xem nhé. Đầu tiên mình sẽ chọn thử c = 600 xem sao nhé.
Áp dụng vào công thức ta được:

Vậy là chúng ta đã có được phép tính đầu tiên với
input = kilomet = 3
Hằng số c = 600
output = met = 1800
Nhưng thực tế giá trị mong muốn đầu ra của chúng ta phải là 3000 chứ không phải là 1600 như ban nãy. Và trong Học máy người ta gọi sự sai khác này là Lỗi (Error). Từ bên trên ta có được
Error = Giá trị thật - giá trị đã dự đoán
<=> Error = 3000 - 1800
<=> Error = 1200
Và từng bước từng bước 1. Ở lần đầu tiên thử ta có Error = 1200 => khá lớn. Và ta cũng biết được nếu chúng ta thay đổi hệ số c thì giá trị output nhận được sẽ lớn hơn. Vậy chúng ta hãy thử tăng hệ số c lên 1 chút xem sao nhé.
Và lần này mình sẽ tăng hệ số c từ 600 -> 900
met = kilomet*c
<=> met = 3 * 900
<=> met = 2700
So sánh với giá trị mong muốn met = 3000 ta được:
Error = 3000 - 2700
<=> Error = 300
=> Vậy là lý thuyết tăng c sẽ giảm Error đã đúng ở trường hợp trên. Vậy liệu nó có luôn đúng và ta sẽ cần tăng c đến bao giờ ? Lần nay ta sẽ tiếp tục tăng c lên 1100 xem sao nhé.
met = kilomet*c
<=> met = 3 * 1100
<=> met = 3300
Error = 3000 - 3100
<=> Error = -300
Giá trị dự đoán của chúng ta đã vượt quá giá trị mà chúng ta mong muốn. Và ở đây ta có Error bằng -300. Ta mong muốn giá trị dự đoán sẽ phải giống hoặc gần giá trị dự đoán nhất. Vậy ta sẽ phải giảm c xuống.
Và cứ thế cứ thế ta tăng giảm hệ số c sao cho giá trị dự đoán gần với giá trị mong muốn nhất và cuối cùng ở đây ta được hệ số c không phải bằng 600,900 hay 1100 mà sẽ là 1000. Test hệ số c = 1000 với trường hợp dòng số 2 của bảng dữ liệu ta nhận được
met = kilomet*c
<=> met = 2 * 1000
<=> met = 2000
Error = 2000 - 2000
<=> Error = 0
Vậy có thể coi hệ số c=1000 này là hoàn hảo với 2 trường hợp test trên.
Và ta có thể nói kilomet phụ thuộc tuyến tính met thông qua hằng số c. Và đây chính là một ví dụ về hồi quy tuyến tính.
Nếu ta hiển thị trên hệ trục tọa độ, ta được hình dưới đây.
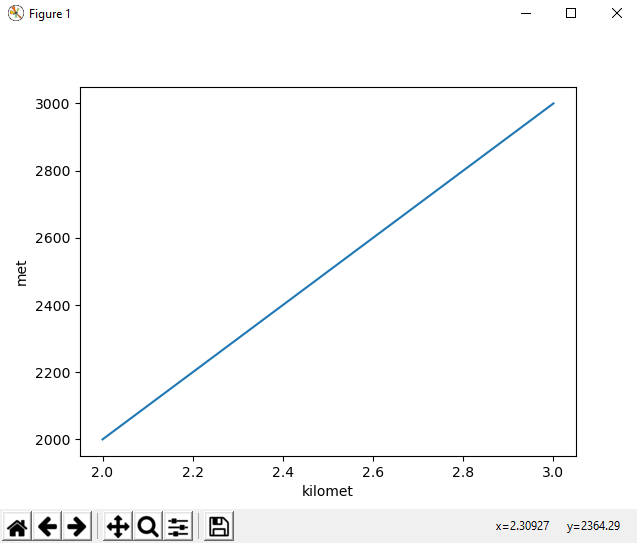
Code python:
import matplotlib.pyplot as plt
plt.plot([2, 3], [2000, 3000])
plt.xlabel('kilomet')
plt.ylabel('met')
plt.show()
Quan hệ giữa met và kilomet đang được hiển thị bằng hàm số có đường thẳng y = c*x màu xanh trên hình, trong đó có c = 1000, x và y lần lượt là kilomet và met.
Áp dụng vào bài toán phân loại tuyến tính
Khác với bài toán hồi quy, khi ta có giá trị của y trong hàm số y=cx phụ thuộc tuyến tính vào c thì trong bài toán phân loại tuyến tính. Công việc của chúng ta cơ bản vẫn là tìm các hệ số c của hàm số phân lớp.
Xét ví dụ với hình ở bên dưới thì công việc của chúng ta làm với bài toán phân loại tuyến tính vẫn chỉ là tìm ra hệ số c của hàm số (ường màu đen) để ngăn cách giữa 2 lớp class mà thôi.
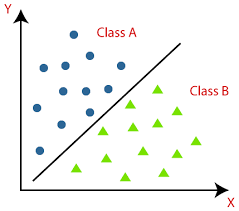
Kết luận:
Công việc "học" trong học máy chỉ là việc thay tăng giảm giá trị của hằng số đã được cho để tìm ra một hàm số
Ví dụ bên trên chỉ là ví dụ "học" với duy nhất 1 cặp dữ liệu để giúp bạn hình dung ra bên trong nó sẽ "học" thế nào. Trên thực tế có nhiều cặp dữ liệu đi chăng nữa thì lý thuyết cơ bản về học như trên vẫn không thay đổi
Bản chất của bài toán hồi quy, hay phân loại tuyển tính thực chất không khác nhau
*Bài viết còn nhiều thiếu sót. Các bác đọc thấy sai chỗ nào thì comment giúp mình để mình sửa nhé.
References:
- Bài viết được tham khảo từ cuốn sách Make your own neural network - Tariq Rashid
All rights reserved