[Handbook] Linear Regession

Giới thiệu

Hồi quy tuyến tính là một mô hình cơ bản của Học có giám sát trong Machine Learning. Bài viết giới thiệu về cơ sở lý thuyết và các áp dụng thực tế của mô hình hồi quy tuyến tính.

Cơ sở lý thuyết $^{[1]}$

Vấn đề. Cho ma trận $\mathbb{A} \in \mathbb{R}_{m, n}$, vector $\overrightarrow{b} \in \mathbb{R}_{m, 1}$. Tìm vector $\overrightarrow{x}\in\mathbb{R}_{n,1}$ sao cho $||\mathbb{A}\overrightarrow{x} - \overrightarrow{b}||$ đạt giá trị nhỏ nhất.

Ý tưởng: Nếu ta tìm được $\overrightarrow{x}_0$ mà $\mathbb{A}\left(\overrightarrow{x}-\overrightarrow{x}_0\right)$ và $\mathbb{A}\overrightarrow{x}_0-\overrightarrow{b}$ vuông góc với nhau thì:

$$||\mathbb{A}\overrightarrow{x} - \overrightarrow{b}||^2 = ||\mathbb{A}\left(\overrightarrow{x}-\overrightarrow{x}_0\right)||^2 + ||\mathbb{A}\overrightarrow{x}_0-\overrightarrow{b}||^2 \geq ||\mathbb{A}\overrightarrow{x}_0-\overrightarrow{b}||^2$$

Khi đó giá trị nhỏ nhất của $||\mathbb{A}\overrightarrow{x} - \overrightarrow{b}||$ sẽ đạt tại $\overrightarrow{x}_0$.

Hai vector $\mathbb{A}\left(\overrightarrow{x}-\overrightarrow{x}_0\right)$ và $\mathbb{A}\overrightarrow{x}_0-\overrightarrow{b}$ vuông góc đồng nghĩa với $\left(\overrightarrow{x}-\overrightarrow{x}_0\right)^T\left(\mathbb{A}^T\mathbb{A}\overrightarrow{x}_0-\mathbb{A}^T\overrightarrow{b}\right) = 0$, với mọi $\overrightarrow{x} \in \mathbb{R}_{n,1}$

Ta có thể chọn ra $n$ vector $\overrightarrow{x}$ là $\mathbb{X} = \left[\overrightarrow{x}_1-\overrightarrow{x}_0, \overrightarrow{x}_2-\overrightarrow{x}_0, ..., \overrightarrow{x}_n-\overrightarrow{x}_0\right]$ sao cho $\det{X} \ne 0$

Lúc này $\mathbb{X}^T\left(\mathbb{A}^T\mathbb{A}\overrightarrow{x}_0-\mathbb{A}^T\overrightarrow{b}\right) = 0$ nên $\mathbb{A}^T\mathbb{A}\overrightarrow{x}_0-\mathbb{A}^T\overrightarrow{b} = 0$ hay $\overrightarrow{x_0}=\left(\mathbb{A}^T\mathbb{A}\right)^{-1}\mathbb{A}^T\overrightarrow{b}$ với giả sử rằng $\text{rank}\mathbb{A} > 0$

Kết luận. Như vậy để $||\mathbb{A}\overrightarrow{x} - \overrightarrow{b}||$ đạt giá trị nhỏ nhất thì $\overrightarrow{x} = \left(\mathbb{A}^T\mathbb{A}\right)^{-1}\mathbb{A}^T\overrightarrow{b}$

Chú ý. $\left(\mathbb{A}^T\mathbb{A}\right)^{-1}\mathbb{A}^T$ là giả nghịch đảo của $\mathbb{A}$, ký hiệu là $\mathbb{A}^{\dagger}$.

Trong Python, hàm tính giả nghịch đảo này là numpy.linalg.pinv

Áp dụng vào bài toán hồi quy

Bài toán.$^{[2]}$ Trong thí nghiệm xác định hằng số cặp nhiệt điện $C$, ta có công thức $E = E_0 + CT$, trong đó $E$ là suất điện động nhiệt điện và $T$ là nhiệt độ. Ta có bảng số liệu sau:

Công việc của ta là tìm $E_0$ và $C$ tốt nhất.

Đặt $\overrightarrow{w} = \left[E_0, C\right]^T, \overrightarrow{y} = \left[1.16, 1.30, ..., 2.91\right]^T$ và $\mathbb{X} = \left[1, \left[50, 55, ..., 80\right]^T\right]$ trong đó $1$ ký hiệu cho cột toàn số $1$.

Ta muốn $\left(E_0+50C - 1.16\right)^2+(E_0+55C-1.30)^2+...+(E_0+80C-2.91)^2$ là nhỏ nhất

Nói cách khác $||\mathbb{X}\overrightarrow{w}-\overrightarrow{y}||$ là nhỏ nhất, do đó $\overrightarrow{w} = \mathbb{X}^{\dagger}\overrightarrow{y}$

Giải quyết bằng Python.

import numpy as np
import matplotlib.pyplot as plt

X = np.array([[50, 55, 60, 65, 70, 75, 80]]).T
ones = np.ones((7, 1))
Xbar = np.concatenate((ones, X), axis=1) # Ghép thêm cột 1 vào X
y = np.array([[1.16, 1.30, 1.78, 2.00, 2.48, 2.57, 2.91]]).T

Xdagger = np.linalg.pinv(Xbar)
w = np.dot(Xdagger, y)
print("E0 = %f, C = %f" %(w[0][0], w[1][0]))

new_line = np.dot(Xbar, w)
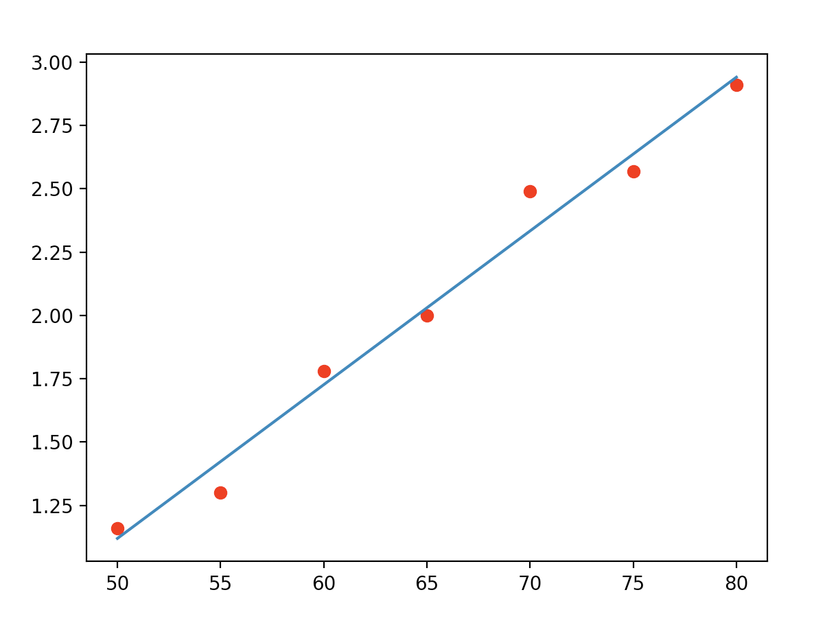
plt.plot(X, y, 'ro')
plt.plot(X, new_line)
plt.show()

Kết quả:

E0 = -1.913214, C = 0.060643

Mở rộng. Ngoài có thể tìm hàm bậc nhất ra, ta có thể tìm các hàm khác phức tạp hơn, miễn sao ta có thể biểu diễn qua phép nhân hai ma trận là được:

Cho các điểm $(-1, 8.5), (0, 2.7), (1, 0.4), (2, -1), (3, -0.2), (4, 3.2), (5, 8.1)$, ta sẽ biểu diễn một đường cong "gần sát" với các điểm trên.

Ta biểu diễn các điểm trên lên đồ thị:

import numpy as np
import matplotlib.pyplot as plt

X = np.array([[-1, 0, 1, 2, 3, 4, 5]]).T
y = np.array([[8.5, 2.7, 0.4, -1, -0.2, 3.2, 8.1]]).T
plt.plot(X, y, 'ro')
plt.show()

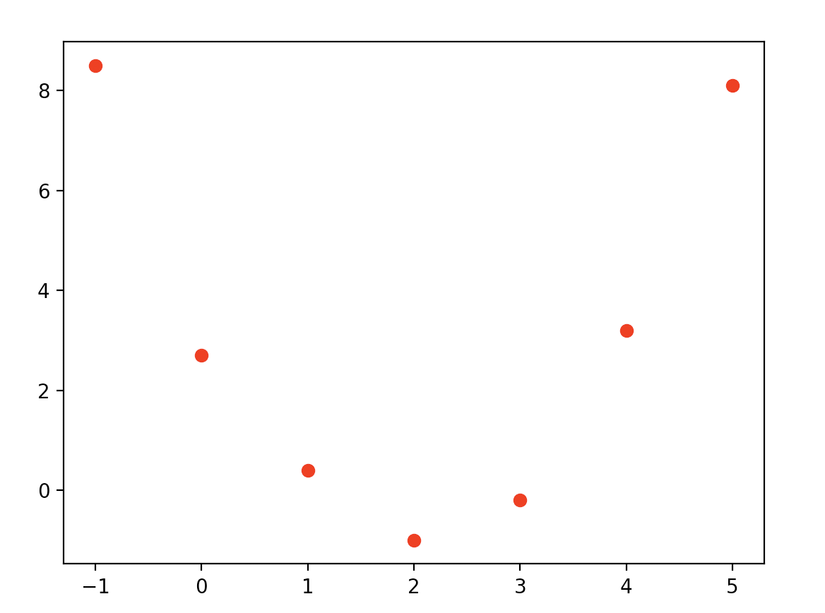
Thấy rằng nó có dạng một Parabol nên ta đoán hàm số có dạng $y=ax^2+bx+c$

Thấy rằng $y = \left[x^2, x, 1\right]\left[a,b,c\right]^T$ nên ta sẽ thêm cột $x^2$ vào và tính kết quả:

import numpy as np
import matplotlib.pyplot as plt

X = np.array([[-1, 0, 1, 2, 3, 4, 5]]).T
y = np.array([[8.5, 2.7, 0.4, -1, -0.2, 3.2, 8.1]]).T
plt.plot(X, y, 'ro')

ones = np.ones((7, 1))
Xbar = np.concatenate((X, X*X), axis=1)
Xbar = np.concatenate((ones, Xbar), axis=1)

Xdagger = np.linalg.pinv(Xbar)
w = np.dot(Xdagger, y)

X = np.linspace(-1, 5, num=20).reshape(20, 1)
ones = np.ones((20, 1))
Xbar = np.concatenate((X, X*X), axis=1)
Xbar = np.concatenate((ones, Xbar), axis=1)

new_line = np.dot(Xbar, w)
plt.plot(X, new_line)
plt.show()

Kết quả không tệ:

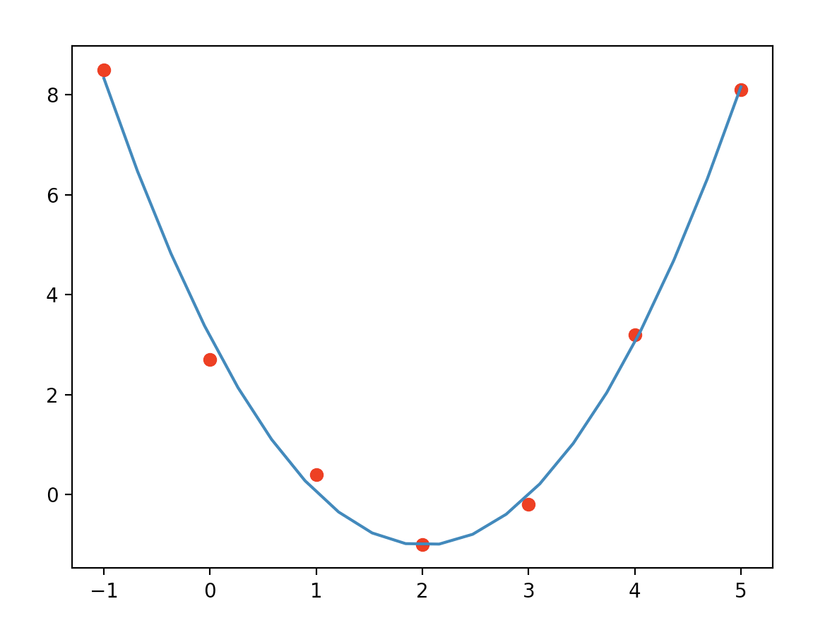
Kết luận.

Qua các ví dụ trên, các bạn cũng phần nào hiểu được cách hoạt động, và khả năng của mô hình Hồi quy tuyến tính, và cho thấy nó có thể áp dụng với nhiều kiểu hàm khác nhau. Tuy nhiên không phải kiểu hàm nào cũng có thể áp dụng được và nếu dữ liệu đầu vào gặp nhiễu thì chúng ra sẽ nhận được kết quả không mong muốn.

Mong rằng với chút kiến thức của mình thì sẽ phần nào giúp các bạn hiểu rõ hơn về mô hình này.

Tài liệu tham khảo.

[1] Advanced Topics in Linear Algebra, The Moore-Penrose Inverse and Least Squares, Ross MacAusland

[2] Thí nghiệm vật lý đại cương A, Nguyễn Minh Châu, Nguyễn Dương Hùng