1. Mô hình ngôn ngữ

Dữ liệu chuỗi là dạng dữ liệu mang có ý nghĩa và mang tính chất tuần tự, như: Âm nhạc, giọng nói, văn bản, phim ảnh, bước đi, ... Nếu chúng ta hoán vị chúng, chúng sẽ không còn mang nhiều ý nghĩa, ví dụ như tiêu đề 'Vợ chồng tỷ phú Bill Gates vừa ly hôn sau gần 30 năm bên nhau' thì mang nhiều ý nghĩa hơn tiêu đề 'Ly hôn tỷ phú vợ chồng Bill Gates sau gần 30 năm bên nhau'.

Dữ liệu dạng văn bản là 1 ví dụ điển hình về dữ liệu chuỗi. Mỗi bài post trên facebook là một chuỗi các từ, cũng là chuỗi các ký tự. Dữ liệu văn bản là dạng dữ liệu quan trọng cùng với dữ liệu hình ảnh trong lĩnh vực học máy.

Việc tiền dữ lý dữ liệu văn bản gồm 4 bước:

• Nạp dữ liệu văn bản ở dạng chuỗi vào bộ nhớ
• Chia chuỗi vừa nạp thành các token, mỗi token là 1 từ hoặc 1 ký tự
• Xây dựng bộ từ vựng để ánh xạ các token thành chỉ số để phân biệt chúng với nhau (token_to_idx)
• Ánh xạ tất cả token trong văn bản thành các chỉ số tương ứng để dễ dàng đưa vào mô hình

Mình có 1 văn bản có độ dài là T, mỗi ký tự là 1 token, nên văn bản là 1 chuỗi các quan sát (các số) rời rạc. Giả sử văn bản trên có dãy token là $x_1, x_2, x_3, ..., x_T$ với $x_t(1\leq t\leq T)$ được coi là đầu ra tại bước thời gian $t$, khi đã có chuỗi thời gian trên, mục tiêu của mô hình phải tính được xác suất của:

$$p(x_1, x_2, .., x_T)$$

Một mô hình ngôn ngữ lý tưởng có thể tự tạo ra văn bản tự nhiên bằng việc chọn $w_t$ ở bước thời gian $t$ với $w_t \sim p(w_t\mid w_{t-1}, ..., w_1)$

Vậy làm thể nào để mô hình hóa một tài liệu hay thậm chí là 1 chuỗi các từ. Chúng ta sẽ áp dụng quy tắc xác suất cơ bản sau:

$$p(Statistics, is, fun, .) = p(Statistics) * p(is \mid Statistics) * p(fun \mid Statistics, is) * p(. \mid Statistics, is, fun)$$

Mình cùng nhớ lại mô hình Markov và áp dụng để mô hình hóa ngôn ngữ. Một phân phối trên các chuỗi thỏa mãn điều kiện Markov bậc một nếu $p(w_{t+1} \mid w_t, ..., w_1) = p(w_{t+1} \mid w_t)$. Các bậc cao hơn ứng với các chuỗi phụ thuộc dài hơn. Do đó, chúng ta có thể áp dụng xấp xỉ:

$$p(w_1, w_2, w_3, w_4) = p(w_1) * p(w_2) * p(w_3) * p(w_4)$$

$$p(w_1, w_2, w_3, w_4) = p(w_1) * p(w_2 \mid w_1) * p(w_3 \mid w_2) * p(w_4 \mid w_3)$$

$$p(w_1, w_2, w_3, w_4) = p(w_1) * p(w_2 \mid w_1) * p(w_3 \mid w_1, w_2) * p(w_4 \mid w_2, w_3)$$

Các công thức xác suất trên lần lược được gọi là unigram, bigram và trigram. Các công thức này đều có dạng n-gram.

2. Mạng Neural hồi tiếp

Như mô hình n-gram mình vừa tìm hiểu phía trên, xác suất có điều kiện của từ $x_t$ tại vị trí $t$ chỉ phụ thuộc vào $n-1$ từ trước đó. Rõ ràng là muốn kiểm tra xem 1 từ ở vị trí phía trước vị trí $t-(n-1)$, ta sẽ phải tăng n lên theo, đồng nghĩa với số tham số mô hình sẽ tăng theo hàm mũ vì ta cần lưu $\lvert V \rvert ^ n$ giá trị với 1 từ điển $V$ nào đó. Do đó, sẽ tốt hơn nếu chúng ta dùng mô hình biến tiềm ẩn:

$$p(x_t \mid x_{t-1}, ..., x_1) \approx p(x_t \mid x_{t-1}, h_t)$$

$h_t$ được gọi là trạng thái ấn, để lưu các thông tin của chuỗi cho đến thời điểm hiện tại. Trạng thái ẩn $h_t$ được tính bằng cả $x_t$ và trạng thái ẩn trước đó $h_{t-1}$:

$$h_t = f(x_t, h_{t-1})$$

Việc dùng thêm trạng thái ẩn có thể khiến việc tính toán và lưu trữ của mô hình trở nên nặng nề.

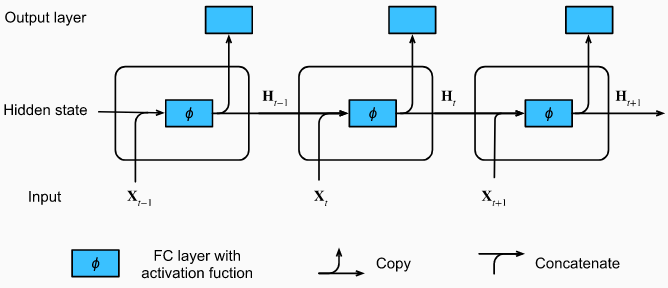
Ở đây, $t$ được gọi là bước thời gian. Với mỗi $t$ ta có $\bold{X}_t \isin \Bbb{R} ^ {n * d}$ và $\bold{H}_t \in \Bbb{R} ^ {n * h}$ là trạng thái ẩn ở bước thời gian $t$ của chuỗi. Ở đây ta dùng thêm $\bold{W}_{hh} \in \Bbb{R} ^ {h * h}$ để làm tham số mô tả cho việc dùng trạng thái ẩn trước đó cho dự đoán ở bước thời gian hiện tại:

$$\bold{H_t} = \phi(\bold{X}_t \bold{W}_{xh} + \bold{H}_{t-1} \bold{W}_{hh} + b_h)$$

Chúng ta có đầu ra khá giống với perceptron đa tầng:

$$\bold{O}_t = \bold{H}_t \bold{W}_{hq} + b_q$$

Ở đây sau khi kết nối đầu vào $\bold{X}_t$ với trạng thái ẩn trước đó ${H}_{t-1}$, ta coi nó như 1 input đầu vào của 1 tầng kết nối đầy đủ với hàm kích hoạt $\phi$, đầu ra là trạng thái ẩn ở bước thời gian hiện tại $H_t$. $H_t$ được dùng để tính $H_{t+1}$ là trạng thái ẩn ở bước thời gian tiếp theo, đồng thời được dùng để tính giá trị đầu ra ở bước thời gian hiện tại.

3. Mạng hồi tiếp nút có cổng

Từ công thức phần 2, ta rút ra:

$$h_t=f(x_t, h_{t-1}, w_h)$$

$$o_t = g(h_t, w_o)$$

Ta có chuỗi các giá trị $\{..., (h_{t-1}, x_{t-1}, o_{t-1}), (h_t, x_t, o_t)\}$ phụ thuộc nhau và có tính chất đệ quy. Vì tính chất này, với nhiều bước thời gian thì có thể gây ra hiện tượng tiêu biến hoặc bùng nổ gradient.

Ta sẽ gặp các tình huống như sau:

• Ta gặp 1 quan sát xuất hiện sớm và ảnh hưởng rất lớn đến toàn bộ các quan sát phía sau. Thường thì ta phải gán 1 giá trị cực lớn cho gradient của quan sát ban đầu đó, nhưng ta có thể dùng 1 cơ chế để lưu thông tin quan trọng ở quan sát ban đầu vào ô nhớ.

• Tình huống khác là các quan sát phía trước không mang nhiều ý nghĩa để phục vụ cho việc dự đoán các quan sát phía sau, như khi phân tích 1 trang HTML ta có thể gặp thẻ <mark> nhưng nó không giúp gì cho việc truyền tải thông tin. Do đó, ta muốn bỏ qua những ký tự như vậy trong các biểu diễn trạng thái ẩn

• Với các văn bản có các chương, khi xuống dòng chuyển qua chương mới thì ta muốn đặt lại các trạng thái ẩn về ban đầu, bởi hầu như ý nghĩa của chương phía sau không liên quan đến chương phía trước.

Có rất nhiều ý tưởng để giải quyết các vấn đề trên, một trong những phương pháp ra đời sớm nhất là Bộ nhớ ngắn hạn dài (LSTM), nút hồi tiếp có cổng (GRU) là 1 biến thể khác của LSTM, thường có chất lượng tương đương nhưng tốc độ tính toán nhanh hơn đáng kể.

Khác biệt chính giữa RNN thông thường và GRU là GRU cho phép điều khiển trạng thái ẩn, tức là ta có các cơ chế học để xem khi nào nên cập nhật và khi nào nên xóa trạng thái ẩn. Ví dụ như với các quan sát quan trọng, mô hình sẽ học để giữ nguyên trạng thái ẩn của quan sát đó. Với nhưng quan sát không liên quan, mô hình sẽ xóa bỏ qua các trạng thái ẩn đó khi cần thiết.

Cổng xóa và cổng cập nhật

GIả sử ta có biến xóa và biến cập nhật, biến xóa cho phép kiểm soát bao nhiêu phần mà trạng thái trước đây được giữ lại, biến cập nhật cho phép kiểm soát trạng thái ẩn mới có bao nhiêu phần giống trạng thái ẩn cũ.

Ta sẽ đi thiết kế các cổng cho các biến đó, với đầu vào ở bước thời gian hiện tại là $\bold{X}_t$ và trạng thái ẩn ở bước trước đó $\bold{H}_{t-1}$, ta sẽ có 2 biến đại diện cho 2 cổng: cổng xóa $\bold{R}_t \in \Bbb{R} ^ {n*h}$ và cổng cập nhật $\bold{Z}_t \in \Bbb{R} ^ {n*h}$, được tính như sau:

$$\bold{R}_t = \sigma(\bold{X}_t\bold{W}_{xr} + \bold{H}_{t-1}\bold{W}_{hr} + \bold{b}_r)$$

$$\bold{Z}_t = \sigma(\bold{X}_t\bold{W}_{xz} + \bold{H}_{t-1}\bold{W}_{hz} + \bold{b}_z)$$

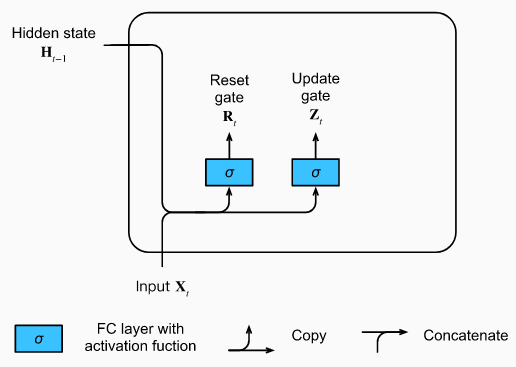
Trong đó, $\bold{W}_{xr}, \bold{W}_{xz} \in \Bbb{R} ^ {d*h}$ và $\bold{W}_{hr}, \bold{W}_{hz} \in \Bbb{R} ^ {h*h}$ là các trọng số và $\bold{b}_r, \bold{b}_z \in \Bbb{R}^{1*h}$ là các tham số độ chênh. Dùng hàm sigmoid để 2 giá trị thu được $\in (0, 1)$

Hoạt động của cổng xóa

Quay trở lại với công thức thông thường của RNN:

$$\bold{H}_t = \tanh (\bold{X}_t\bold{W}_{xh} + \bold{H}_{t-1}\bold{W}_{hh} + \bold{b}_h)$$

Với hàm kích hoạt là hàm $tanh$ để giá trị $\in (-1, 1)$

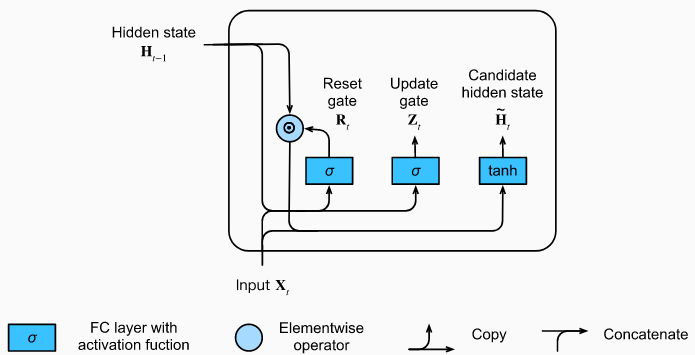
Để giảm ảnh hưởng của trạng thái ẩn trước đó, ta có công thức sau:

$${\tilde{\bold{H}}}_t = \tanh (\bold{X}_t\bold{W}_{xh} + (\bold{R}_t \odot \bold{H}_{t-1})\bold{W}_{hh} + \bold{b}_h)$$

Ta thấy $\bold{R}_t$ gần 0 thì trạng thái ẩn đầu ra chính là output của multiperceptron 1 tầng với input là $\bold{X}_t$ và các trạng thái ẩn trước đó đều đặt về mặc định, nên {\tilde{\bold{H}}}_t được gọi là trạng thái ẩn tiềm năng. Ngược lại nếu gần 1, thì công thức lại quay trở về RNN thông thường.

Hoạt động của cổng cập nhật

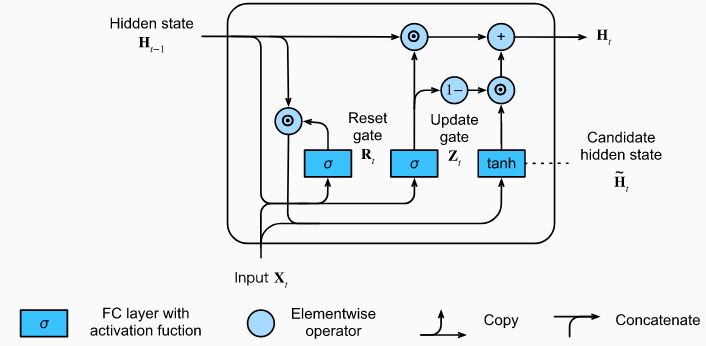
Cổng cập nhật xác định mức giống nhau giữa trạng thái ẩn hiện tại $\bold{H}_t$ và $\bold{H}_{t-1}$

$$\bold{H}_t = \bold{Z}_t \odot \bold{H}_{t-1} + (1 - \bold{Z}_t) \odot {\tilde{\bold{H}}}_t$$

Nếu giá trị của $\bold{Z}_t$ bằng 1 thì $\bold{H}_t = \bold{H}_{t-1}$. Trong trường hợp này, thông tin của $\bold{X}_t$ sẽ bị bỏ qua, tương đương với việc bỏ qua bước thời gian $t$ trong chuỗi thời gian. Ngược lại, nếu $\bold{Z}_t$ bằng 0, thì trạng thái ẩn $\bold{H}_t$ sẽ gần giống với trạng thái ẩn tiềm năng ${\tilde{\bold{H}}}_t$

Những thiết kế trên có thể giúp mô hình RNN giải quyết vấn đề triệt tiêu hoặc bùng nổ gradient và nắm bắt tốt hơn các thông tin của các quan sát trong chuỗi thời gian.

4. Kết luận

• Mạng neural hồi tiếp với nút có cổng có thể nắm bắt được các phụ thuộc từ các quan sát xa trong chuỗi thời gian.

• Cổng xóa giúp nắm bắt các phụ thuộc ngắn hạn trong chuỗi thời gian

• Cổng cập nhật giúp nắm bắt các phụ thuộc dài hạn trong chuỗi thời gian.

• Nếu GRU có cổng xóa không được kích hoạt, nó lại trở về mô hình RNN thông thường.

Tài liệu tham khảo

• Dive into Deep Learning (d2l)

• understanding-gru-networks