Giữa Convolutional Neural Network, Transformer và Graph Neural Network

Caveat

Công thức của một lớp tích chập trong Convolutional Neural Network(CNN) có thể được viết dưới dạng như Hình 1:

Hình 1: Góc nhìn thứ nhất của lớp tích chập trong CNN.

Nếu bạn không quen thuộc với cách viết trên, nhưng đã biết về cách biểu diễn như Hình 2:

Hình 2: Góc nhìn thứ hai của lớp tích chập trong CNN(Nguồn: https://cs231n.github.io/convolutional-networks/).

thì bạn có thể đọc chứng minh ở phần Phụ chú cho một trường hợp đơn giản trước khi đi tiếp. Ngược lại, mời đọc phần "Giữa Convolutional Neural Network, Transformer và Graph Neural Network".

Phụ chú: Hai góc nhìn của lớp tích chập trong Convolutional Neural Network

Giả sử kích cỡ kernel là 3x3, số lượng kernel là 2(cho đơn giản). Gọi X là đầu vào, được pad tại biên như Hình 3 (nửa trên)(nhằm làm cho kích cỡ đầu vào và kích cỡ đầu ra giống nhau, do đó dễ đánh chỉ số hơn mà thôi). Gọi Y là đầu ra của lớp tích chập trước khi đi qua hàm phi tuyến. Cách đánh chỉ số cho tensor đầu vào và đầu ra được mô tả như Hình 3 (nửa trên). Ta có đẳng thức như ở Hình 3 (nửa dưới), tuân theo đúng góc nhìn thứ hai (Hình 2):

Hình 3: Tiền đề.

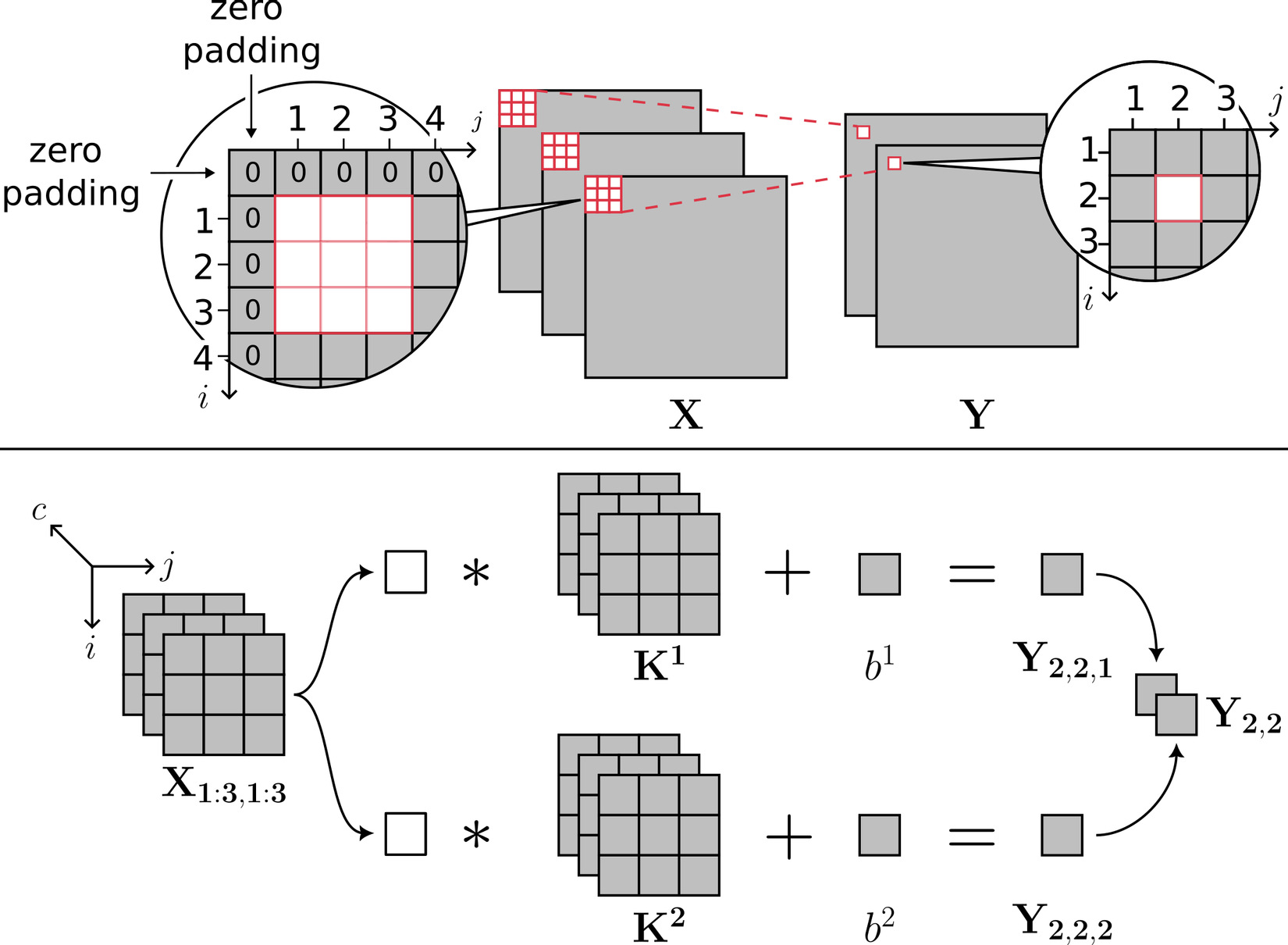
Ta có lập luận như Hình 4 để đưa công thức ở Hình 3 về dạng góc nhìn thứ nhất.

Hình 4: Chuyển từ góc nhìn thứ hai sang góc nhìn thứ nhất.

Giữa Convolutional Neural Network, Transformer và Graph Neural Network.

Hình 5 mô tả trực quan hoạt động của một lớp tích chập trong CNN và lớp Transformer Encoder đầu tiên của kiến trúc Transformer. Lưu ý, để cho đơn giản, người viết chỉ mô tả phần Attention của Transformer Encoder và cũng bỏ qua phần chuẩn hoá tích query-key.

Hình 5: Giữa CNN và Transformer.

1. Unroll các toán tử ma trận trong CNN và Transformer thành vòng lặp của phép kết tập chia sẻ tham số.

Có thể thấy, lớp tích chập và cơ chế Attention đều hoạt động theo mô thức như sau: lặp trên từng đơn vị của dữ liệu đầu vào (pixel đối với CNN, token đối với Transformer); tại mỗi đơn vị đó gom các đơn vị lân cận thành một tập hợp (các pixel nằm trong cửa sổ trượt đối với CNN, toàn bộ các token trong cùng đầu vào đối với Transformer); thực hiện một phép kết tập có tham số (và là tham số học được) để có biểu diễn ẩn của chính đơn vị đang xét; thực hiện các bước như trên với tất cả cho tất cả các đơn vị, với tham số của phép kết tập được chia sẻ giữa những bước lặp khác nhau. Như ở ví dụ CNN, đơn vị đang xét là pixel trung tâm với lân cận là 8 pixel hàng xóm và chính nó (vì biểu diễn của nó cũng được dùng làm đầu vào cho phép kết tập). Ở ví dụ Transformer, đơn vị đang xét là token "tìm" với lân cận là cả 4 token trong cùng câu: "tôi"(chủ ngữ), "đi", "tìm" và "tôi"(tân ngữ), tức bản thân token "tìm" và tất cả các token còn lại.

Sau phép kết tập, thông tin về lân cận (tức thông tin để trả lời câu hỏi "Đơn vị nào là có quan hệ lân cận với đơn vị nào?"), nói chung là không thay đổi. Ngoại trừ với những đơn vị ở biên của phép tích chập, các pixel còn lại (chiếm phần lớn hơn cả) không có sự thay đổi về lân cận.

Đối với các bài toán liên quan đến dữ liệu ảnh và dữ liệu văn bản, thông tin về toạ độ của mỗi đơn vị là quan trọng. Chưa kể đến yêu cầu bất biến với phép quay, phép lật gương khi thực hiện tích chập, thì nói chung các W_i,j là khác nhau, tức trọng số cho các pixel ở những hướng khác nhau trong toạ độ 2 chiều là khác nhau. Tương tự, đối với dữ liệu văn bản, thứ tự (tương đối với các token khác) khác nhau của cùng một token làm thay đổi vai trò của token như. Như ở ví dụ Hình 5, token "tôi" có thể là chủ ngữ nhưng cũng có thể là tân ngữ. Thành phần Token Embedding là chưa nhúng thông tin về thứ tự của token. Để bù lại, Transformer sử dụng Positional Embedding (duy nhất một lần ở lớp đầu tiên của Encoder hoặc Decoder).

2. Biểu diễn dữ liệu ảnh và văn bản dưới dạng đồ thị.

Khái niệm "lân cận" nhắc đi nhắc lại ở trên là căn bản cho một kiểu dữ liệu, đó là đồ thị. Trong đồ thị có các đơn vị là các đỉnh, và các cạnh nối các đỉnh thể hiện mỗi quan hệ lân cận giữa các đỉnh với nhau. Ta có thể mô hình hoá dữ liệu ảnh và dữ liệu văn bản thành dạng đồ thị như ở Hình 6.

Hình 6: Dữ liệu ảnh và văn bản dưới dạng đồ thị.

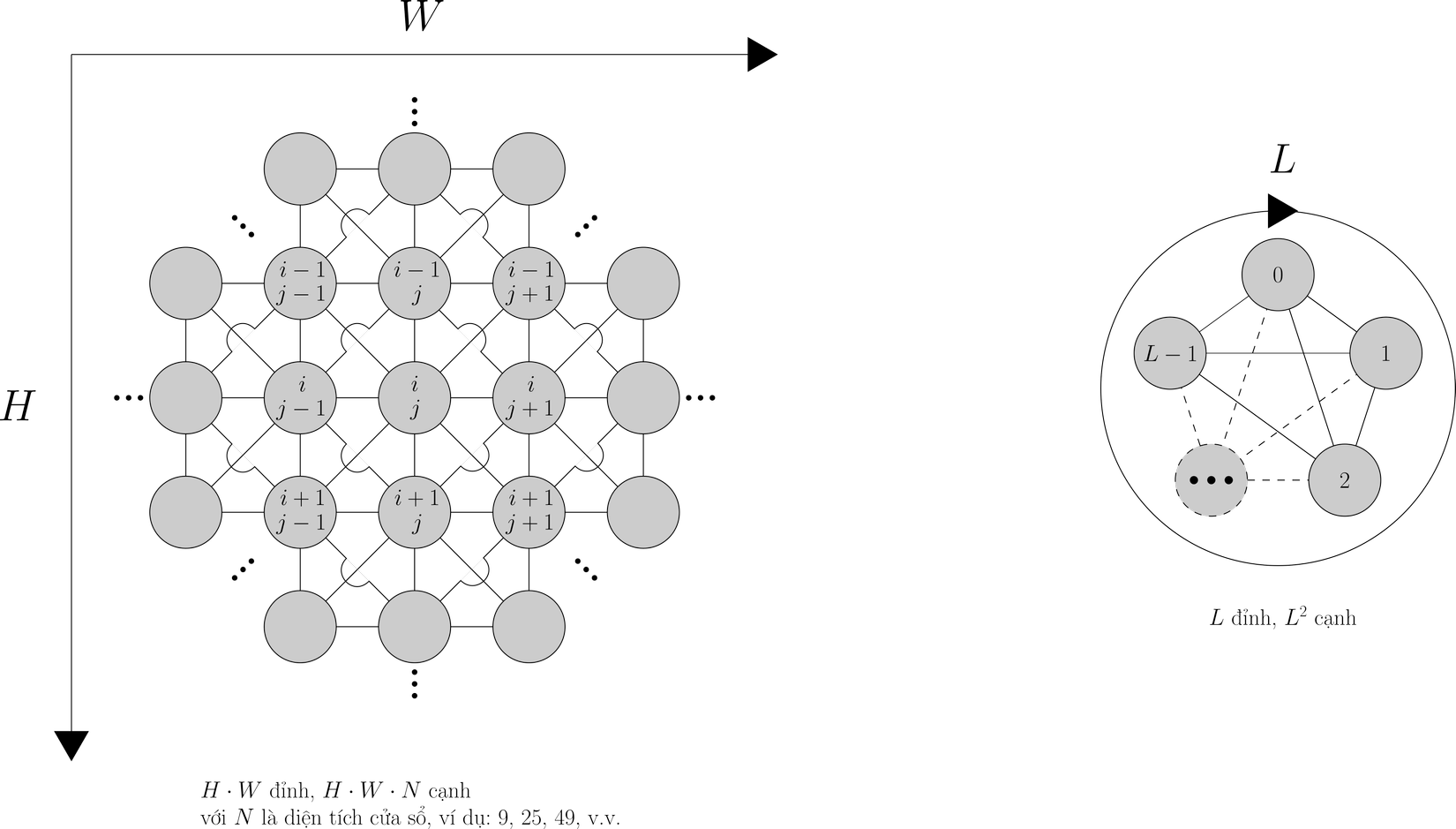
Cần lưu ý rằng, việc xác định tồn tại hay không cạnh nối đỉnh này tới đỉnh kia là không đơn giản. Dạng đồ thị cho ảnh được vẽ cho trường hợp kernel có kích cỡ 3x3, còn dạng đồ thị cho văn bản được vẽ cho trường hợp một token sẽ attend tới tất cả các token còn lại như ở Transformer, do đó nó là một đồ thị đầy đủ. Gắn trên mỗi đồ thị là một hệ toạ độ rời rạc xác định toạ độ hay vị trí của token. Như đã thấy ở phần 1, nhiều khi lân cận của một đỉnh sẽ bao gồm chính nó. Cạnh nối một đỉnh với chính nó gọi là khuyên. Khuyên tồn tại ở cả trường hợp CNN và Transformer, Hình 6 không vẽ khuyên để tránh rối rắm, người đọc xin lưu ý điều này.

Hình 7 và Hình 8 tổng kết lại góc nhìn kết tập đồ thị của CNN và Transformer.

Hình 7: Vòng lặp kết tập dựa trên lân cận đồ thị của CNN.

Hình 8: Vòng lặp kết tập dựa trên lân cận đồ thị của Transformer.

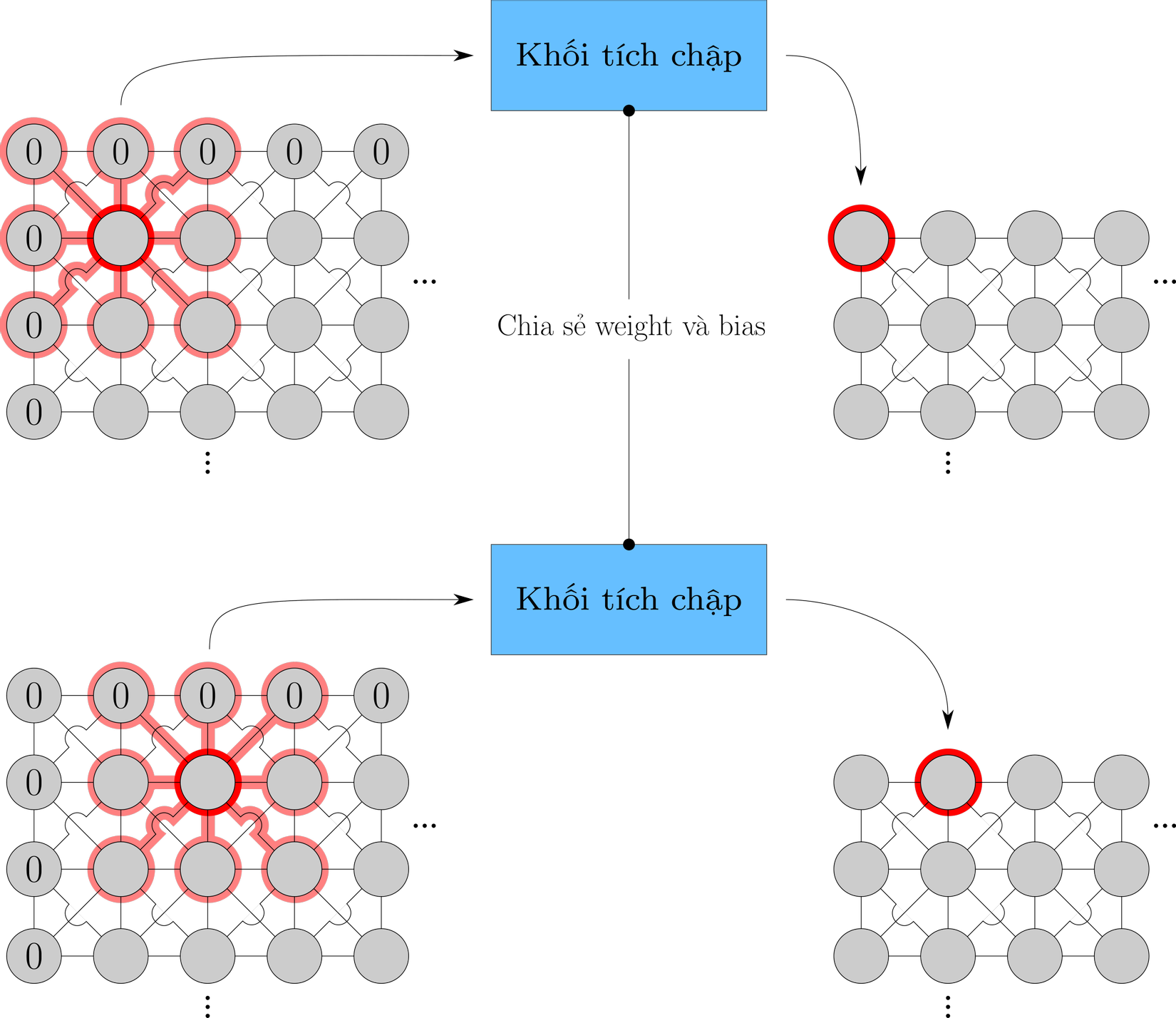
3. Ví dụ đơn giản cho một Graph Neural Network.

Vậy với một đồ thị bất kỳ(Hình 8), không có dạng mạng lưới như ở CNN và cũng không phải kết nối đầy đủ như ở Transformer thì có thể áp dụng neural network như thế nào?

Hình 8: Ví dụ của một đồ thị với đặc trưng đỉnh.

Trước hết, ta có thể định nghĩa đầu vào và đầu ra theo lân cận(Hình 9).

Hình 9: Đầu vào và đầu ra của khối kết tập đồ thị.

Về cơ chế bên trong của khối kết tập, ta "mượn" công thức của CNN. Giả sử chỉ có thông tin về quan hệ lân cận mà không có thông tin về vị trí tương đối giữa các đỉnh, hoặc ta tạm thời cố tình không quan tâm đến thông tin về vị trí tương đối giữa các đỉnh cho đơn giản, khi đó các đỉnh phải dùng chung một ma trận W(Hình 10).

Hình 10: Công thức kết tập đề xuất cho mạng neural network xử lý dữ liệu đồ thị (1).

Biến đổi lại cho gọn gàng, ta có lớp kết tập đồ thị như Hình 11.

Hình 11: Công thức kết tập đề xuất cho mạng neural network xử lý dữ liệu đồ thị (2).

Kiến trúc này là một khởi đầu không quá tệ, nó khá giống với ví dụ đơn giản của nhà nghiên cứu Thomas Kipf(Hình 12). Cụ thể, kiến trúc của chúng ta có sử dụng kết nối khuyên và bias, còn ví dụ của tác giả Graph Convolutional Network không có thành phần bias.