1. Bài toán K-nearest neighbor.

1.1 Bài toán.

Bạn là một chú ong nhỏ bé, bạn bay khắp nơi và lấy mật từ những bông hoa iris. Nhưng có một vấn đề khá lớn, có 3 loại hoa iris là setosa, virginica và versicolor, mỗi một kiểu hoa trên đều sản xuất ra các loại mật khác nhau. Bạn đã từng bay và lấy mật của 150 bông hoa (50 bông mỗi loại) nên bạn cũng đã có kinh nghiệm về việc phân loại các loài hoa trên.

Cấp báo: Bên tổ chức trinh sát các loài ong vừa kiếm được một lô hoa mới, cần gấp các chú ong tinh nhuệ có thể phân loại được 3 loại hoa trên.

Ngay tức tốc bạn di chuyển đến để có thể hỗ trợ việc phân loại 3 loại hoa trên để có thể lấy được đúng loại mật cần thiết. Bạn nghĩ ra được một cách rất hay, 3 loại hoa trên đều có các thông số như sau [sepal lenght, sepal width, petal length, petal width], khi gặp một bông hoa mới, bạn chỉ cần lấy các thông số như trên và đem so sánh với những loại hoa mà bạn đã biết, bông hoa mới sẽ chính là loại hoa giống với nó nhất.

1.2 Thuật toán KNN.

Như ở ví dụ trên, ta sẽ đem tất cả những bông hoa mới đem so sánh với những bông hoa đã biết và gắn nhãn bông hoa mới bằng nhãn với k bông hoa đã biết tương tự nó, giờ ta sẽ phải hiểu như thế nào là giống nhau. Trong bài toán trên tôi sẽ lấy 2 giá trị là petal length và petal width để dễ nói hơn, ta có 2 bông hoa biết trước như sau:

hoa loại 1: [1.4, 0.2]

hoa loại 2: [4.7, 1.4]

hoa mới chưa biết: [3, 0.5]

Cách thức tính độ giống nhau giữa hoa chưa biết với cả hoa loại 1 và loại 2 như sau, ta coi các điểm trên là một vector và có thể mô phỏng ở trên trục tọa độ như hình dưới. Có thể thấy rõ ràng rằng các điểm ở trên trục càng gần nhau thì sẽ càng giống nhau.

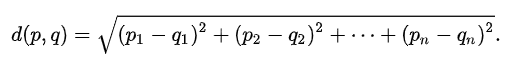
Để có thể tính toán được khoảng cách trên ta sẽ sử dụng euclidean distance.

Ta sẽ sử dụng công thức trên để tính thử xem loại hoa mới có độ tương quan với loại 1 và loại 2 như nào.

Hoa loại 1 và hoa mới:

Hoa loại 2 và hoa mới:

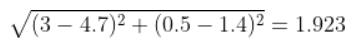
Ta thấy ngay rằng bông hoa mới sẽ giống hoa loại 1 hơn vì nó gần với giá trị của hoa loại 1 hơn. Nhưng trong thực tế việc ta dự đoán như vậy nó sẽ không hợp lý, vì chưa chắc bông hoa gần nhất đã là loại hoa chuẩn. Để giải quyết vấn đề này tham số K đã được đưa vào, K là tham số thể hiện số lượng bông hoa gần với bông hoa mới nhất. Ví dụ ta đã có thông số của hoa mới với hoa loại 1 và loại 2 là [1.627, 1.923].T, tôi lấy k = 1 thì tỷ lệ hoa mới sẽ là [1, 0, 0] với 3 loại hoa được xếp tuần tự từ trái sang phải (1 là 100% loại 1, 0 là 0 % loại 2, 0 là 0 % loại 3), với k = 2 thì tỉ lệ hoa mới sẽ là [0.5, 0.5, 0].

Vậy là ta đã hoàn thiện thuật toán K-nearest neighbor với các bước như sau:

1. Tính khoảng cách của dữ liệu mới với những dữ liệu đã biết.
2. Đưa tất cả các khoảng cách trên vào một matrix và sắp xếp từ bé đến lớn.
3. Lấy K điểm nhỏ nhất ở matrix bên trên để tính tỷ lệ.
4. Đưa ra đáp án.

2. Ngồi lại rồi code nào!!

class knn:
    def __init__(self, data):
        """
        Data sẽ là những gì mà chú ong đã biết trước.
        Tôi sẽ mặc định một điểm dữ liệu sẽ có dạng như sau:
        [<target>,[<value>]]
        Ví dụ: ["setosa",[1.5,0.4]]
        với index = 0 sẽ là loại.
        với index = 1 sẽ là các giá trị.
        """
        self.data = data
    
    #func tính Euclidean distance.
    def euclidean_distance(self, pointA, pointB):
        distance = 0
        for i in range(len(pointA)):
            distance += (pointA[i] - pointB[i])**2
        return distance**(1/2)

    # Tạo matrix chứa khoảng cách và loại.
    def generate_matrix(self, new_point):
        matrix = [] #tạo matrix rỗng.
        for value in self.data:
            mtr_point = [] #tạo điểm dữ liệu.
            mtr_point.append(value[0])
            mtr_point.append(self.euclidean_distance(pointA = new_point,pointB = value[1]))
            matrix.append(mtr_point) #đưa điểm dữ liệu vào matrix.
        matrix.sort(key= lambda x: x[1]) #sort matrix.
        return matrix

    # Func dự đoán.
    def predict(self, new_point, k = 2):
        # tạo matrix.
        matrix = self.generate_matrix(new_point)
        # lấy k điểm gần nhất.
        matrix = matrix[:k]
        # lọc ra các loại xuất hiện.
        matrix = [val[0] for val in matrix]
        set_matrix = set(matrix)
        # đưa ra matrix dự đoán.
        predict_matrix = []
        for val in set_matrix:
            count = 0
            for mtr_val in matrix:
                if mtr_val == val:
                    count += 1
            predict_matrix.append([val,count/k])
        predict_matrix.sort(key=lambda x: x[1])
        return predict_matrix

Bên trên là code python của thuật toán knn, bây giờ ta hay sử dụng nó vào tập dữ liệu iris để thử nghiệm nào!

#import thư viện.
from sklearn.datasets import load_iris
import random

#load data
data = load_iris()
#chuẩn hóa dữ liệu và xáo trộn dữ liệu.
target = data.target
iris_data = data.data
data = [[target[i],iris_data[i]] for i in range(len(target))]
random.shuffle(data)

#chia dữ liệu ra tập train và tập test.
train_data = data[:125]
test_data = data[125:]
#khởi tạo model knn.
myknn = knn(data=data)
#thử nghiệm với điểm dữ liệu bất kì. 
print(myknn.predict(test_data[0][1]))
print(test_data[0][0])

Vậy là chúng ta đã làm xong knn, hãy thử nghiệm xem thuật toán này sử dụng với tập dữ liệu hoa iris có độ chính xác như nào.

count = 0 
for val in test_data:
    prediction = myknn.predict(val[1],k=5)
    if prediction[0][0] == val[0]:
        count+=1
print("accuracy:",count/len(test_data)*100,"%")

Mọi người có thể thử nghiệm và đưa kết quả xuống dưới comment.

Vậy là kết thúc cho KNN, theo đánh giá sơ bộ, đây là một thuật toán rất hay nhưng lại gặp một vấn đề rất lớn về bộ nhớ lưu trữ dữ liệu. Không những vậy, mỗi lần ta predict 1 giá trị mới thì sẽ phải quét qua gần như toàn bộ tập dữ liệu, điều này là không cần thiết và rất tốn thời gian. Có lẽ ta sẽ phải có một cách nào đó để giải quyết vấn đề này.