1.7K 82 10

Đã đăng vào thg 9 17, 2020 2:10 SA

trong

10 phút đọc

4.6K

Định train ML/DL model nhưng không biết chọn tham số? Bayesian Optimization!

Giới thiệu

Trong quá trình training model ML hay mạng neural, một bước cực kỳ quan trọng và không thể thiếu là lựa chọn giá trị cho các tham số như learning rate, epochs, số layers, hidden units,... Việc lựa chọn các tham số hợp lý thường dựa trên kinh nghiệm và với mỗi bộ tham số như vậy ta phải huấn luyện model, quan sát kết quả đạt được, đánh giá kết quả, điều chỉnh tham số và lặp lại. Để tự động hóa quy trình trên, các thuật toán tìm kiếm như Grid Search hay Random Search được sử dụng. Tuy nhiên các thuật toán này chỉ hoạt động hiệu quả với số lượng tham số ít, thường là nhỏ hơn 5 vì không gian tìm kiếm sẽ tăng nhanh khi số lượng tham số lớn khiến cho thời gian tìm kiếm trở nên rất lâu. Bayesian Optimization (BO) là một thuật toán giúp tối ưu hiệu quả những hàm mục tiêu có chi phí evaluation lớn (như training 1 mạng neural) dựa trên định lý Bayesian. BO làm giảm đáng kể số lần thử sai khi tune tham số so với Grid Search hay Random Search, điều mà với một mạng deep learning lớn (ResNet, Inception, Xception,..) cùng bộ data khổng lồ (ImageNet) sẽ tốn hàng giờ thậm chí hàng ngày liền. Trong bài này, chúng ta sẽ tìm hiểu cách BO hoạt động và ứng dụng nó tối ưu tham số training model CNN cho bài toán MNIST nhé.

Tổng quan thuật toán

BO tối ưu hàm mục tiêu dựa trên học máy. Viết dưới dạng công thức:

$\max _{x \in A} f(x)$

Trong đó A là tập các tham số cần tune, và số lượng tham số không nên nhiều hơn 20 để đảm bảo thuật toán học tốt nhất; $f(x)$ là hàm mục tiêu để tối ưu lớn nhất/nhỏ nhất (ví dụ: accuracy, loss,...), $f(x)$ có một vài đặc điểm sau:

$f$ là hàm liên tục
Chi phí evaluation của $f$ lớn
$f$ là một black box, ta không hề biết các tính chất của $f$ như tính tuyến tính, hàm lồi, hàm lõm,...
Vì $f$ là một black box, khi thực hiện evaluate $f$ chỉ lấy ra giá trị $f(x)$ , các phương pháp liên quan đến đạo hàm như gradient descent sẽ không khả thi và không được sử dụng.

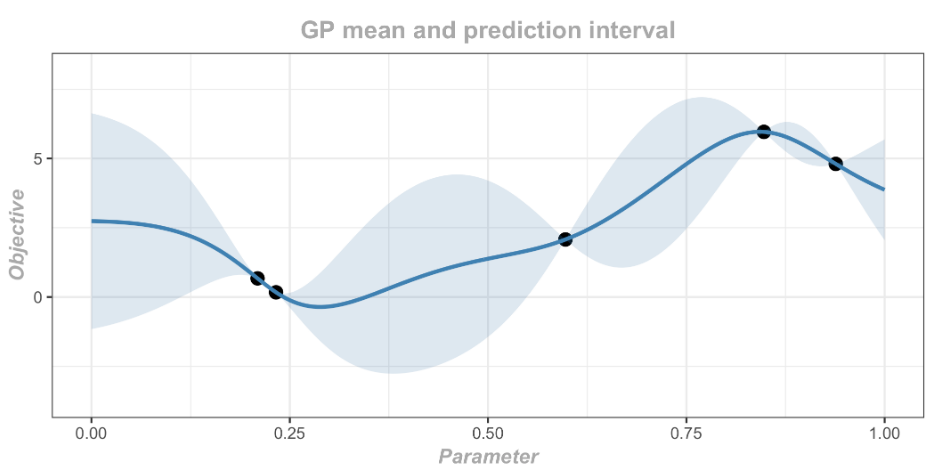
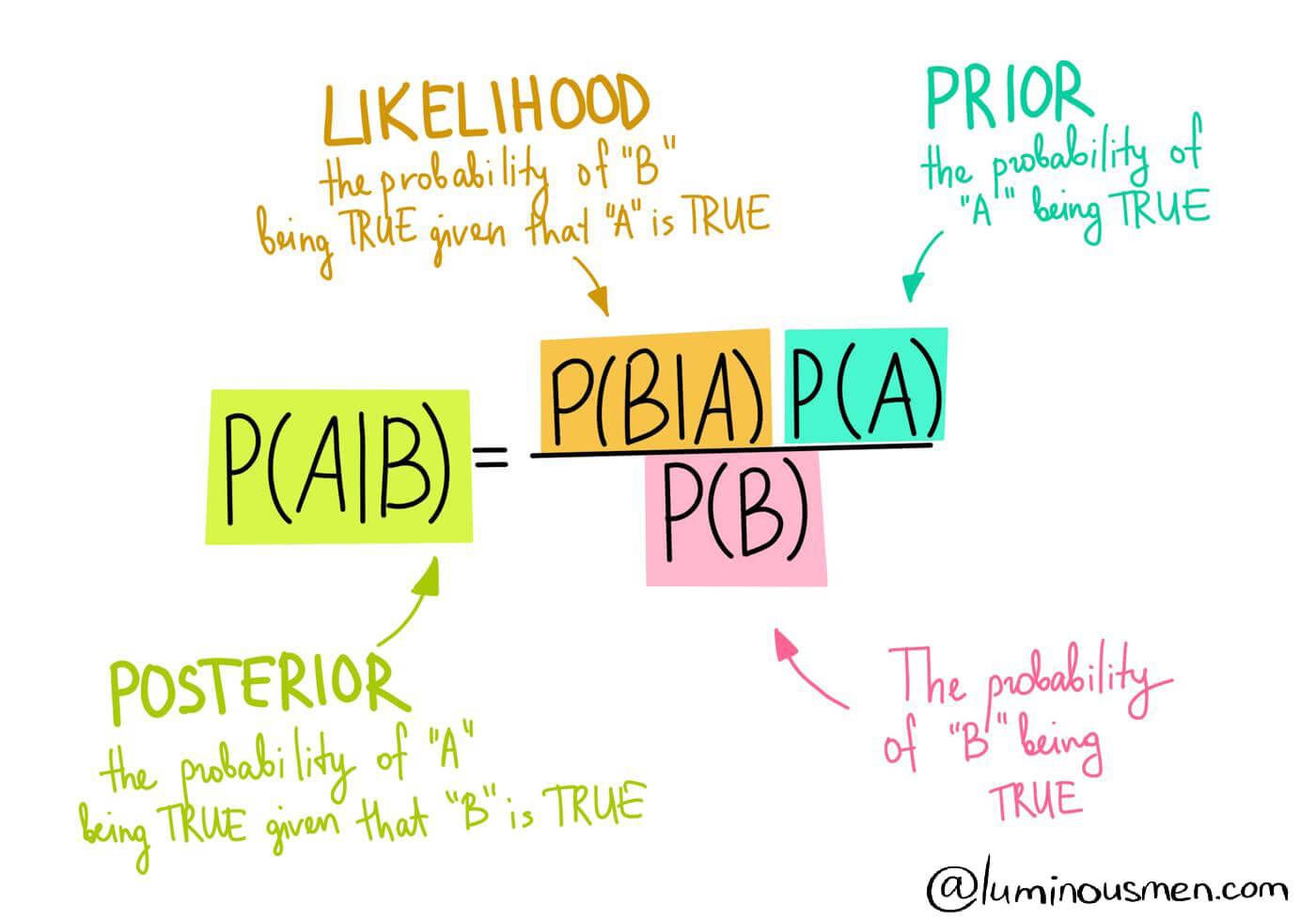
BO xây dựng một hàm surrogate (hàm thay thế) để model $f$ , mục tiêu là tối ưu surrogate càng giống $f$ càng tốt, từ đó có thể tìm ra global minimum/maximum của $f$ dễ dàng bằng cách lấy minimum/maximum của surrogate. Surrogate này là một Gaussian Process với prior distribution và likelihood được định nghĩa từ đầu. Mỗi khi evaluate $f$ của điểm x mới, ta sẽ tính được posterior của surrogate bằng quy tắc Bayes. Dựa trên posterior này, một Acquisition function tìm ra điểm x' có tiềm năng mang lại giá trị $f$ lớn nhất, x' tiếp tục được evaluate và update posterior. Cứ lặp như vậy cho đến khi ta đạt được kết quả $f(x)$ mong muốn.

Pseudo-code cho thuật toán BO:

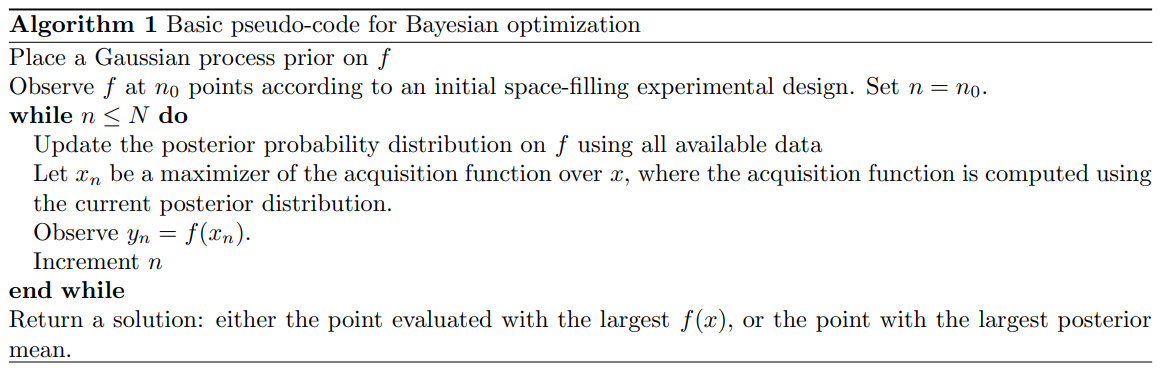
Bước chuẩn bị

Trong bài này mình sẽ sử dụng GPyTorch để implement phần chính của BO là Gaussian Process Regression, mục đích là cung cấp cái nhìn rõ hơn về các thành phần bên trong của GP Regression. Ngoài ra bạn cũng có thể sử dụng luôn model GaussianProcessRegressor của scikit-learn nhé. Cài đặt các thư viện liên quan:

pip install torch torchvision
pip install gpytorch
pip install numpy
pip install scipy
pip install tqdm
pip install ax-platform

Import thư viện:

import numpy as np
from scipy.stats import norm, loguniform
from ax.utils.tutorials.cnn_utils import load_mnist, train, evaluate, CNN
from warnings import catch_warnings
from warnings import simplefilter
from matplotlib import pyplot
from typing import Dict
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader
from tqdm import tqdm

Tiếp đến là hàm để train CNN model trên tập MNIST. Hàm này nhận 1 dict các tham số và giá trị tương ứng và train model bằng các tham số đó, hàm trả về model đã được train. Ở đây mình sẽ chỉ tune 1 tham số duy nhất là learning rate.

def train(
        net: torch.nn.Module,
        train_loader: DataLoader,
        parameters: Dict[str, float],
        dtype: torch.dtype,
        device: torch.device,
) -> nn.Module:
    net.to(dtype=dtype, device=device)
    net.train()
    criterion = nn.CrossEntropyLoss()
    optimizer = optim.SGD(
        net.parameters(),
        lr=parameters.get("lr"),
        momentum=0.9
    )
    num_epochs = 20

    for _ in tqdm(range(num_epochs)):
        for inputs, labels in train_loader:
            inputs = inputs.to(dtype=dtype, device=device)
            labels = labels.to(device=device)
            optimizer.zero_grad()
            outputs = net(inputs)
            loss = criterion(outputs, labels)
            loss.backward()
            optimizer.step()
    return net

Load MNIST data:

torch.manual_seed(12345)
dtype = torch.float
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
BATCH_SIZE = 512
train_loader, valid_loader, test_loader = load_mnist(batch_size=BATCH_SIZE)

Hàm sample_lr generate các giá trị learning rate khác nhau trong khoảng 1e-6 đến 0.2

def sample_lr(size=1):
    return loguniform(0.000001, 0.2).rvs(size)[:, np.newaxis]

Cuối cùng, ta định nghĩa hàm objective chính là hàm số mà ta muốn tối ưu. Cụ thể, hàm này lấy vào x là hyperparameter (learning rate), thực hiện train, evaluate CNN model và trả về giá trị accuracy.

def objective(x):
    parameterization = {"lr": x[0]}
    net = CNN()
    print("Training CNN model....")
    net = train(net=net, train_loader=train_loader, parameters=parameterization, dtype=dtype, device=device)
    acc = evaluate(
        net=net,
        data_loader=valid_loader,
        dtype=dtype,
        device=device,
    )
    print("Accuracy:", acc, "Hyperparams:", parameterization, '\n')
    return acc

Gaussian Process Regression

Gausian Process (GP) Regression là một phương pháp thống kê Bayesian để model các hàm số. GP regression hoạt động hiệu quả trên những tập dataset nhỏ nhờ vào giả định các điểm dữ liệu nằm trên một phân phối nhiều chiều (Multivariate Normal). Đầu tiên ta định nghĩa một GP model, chính là prior distribution trên hàm số. Với một biến ngẫu nhiên X, phân bố của nó được xác định bằng hàm mật độ xác suất (probability distribution function - pdf):

$f\left(x \mid \mu, \sigma^{2}\right)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}$

với $\mu, \sigma$ lần lượt là mean và variance. Khi có nhiều hơn một biến ngẫu nhiên, mean sẽ được biểu diễn dưới dạng 1 vector và variance được biểu diễn dưới dạng ma trận, gọi là covariance matrix. Covariance matrix được xây dựng bằng cách evaluate một hàm covariance hay kernel $Σ_0$ trên từng cặp giá trị $x_i, x_j$ của các biến ngẫu nhiên. Kernel được chọn để các điểm $x_i, x_j$ càng gần nhau trong không gian đầu vào càng có giá trị lớn. Các kernel khác nhau biểu diễn prior khác nhau, dẫn đến hàm số kết quả khác nhau.

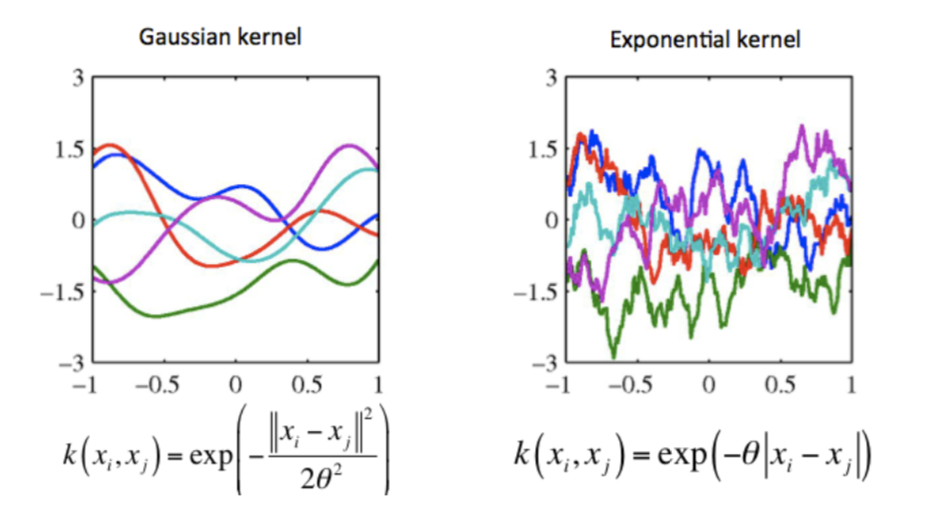
Để xây dựng một prior (GP model) bằng GPyTorch, mình sẽ kế thừa class ExactGP và custom mean cũng như covariance modules. Cụ thể, mình sử dụng ConstantMean và RBFKernel:

import torch
import gpytorch

class ExactGPModel(gpytorch.models.ExactGP):
    def __init__(self, train_x, train_y, likelihood):
        super(ExactGPModel, self).__init__(train_x, train_y, likelihood)
        self.mean_module = gpytorch.means.ConstantMean()
        self.covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())

    def forward(self, x):
        mean_x = self.mean_module(x)
        covar_x = self.covar_module(x)
        return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)

Class Regressor là một GP Regression bao gồm GP model và gaussian likelihood.

class Regressor():
    def __init__(self, train_x, train_y):
        self.training_iter = 100
        self.X = train_x
        self.y = train_y
        self.likelihood = gpytorch.likelihoods.GaussianLikelihood()
        self.gp = ExactGPModel(self.X, self.y, self.likelihood)

    def train(self):
        self.gp.train()
        self.likelihood.train()
        optimizer = torch.optim.Adam([
            {'params': self.gp.parameters()},
        ], lr=0.05)
        mll = gpytorch.mlls.ExactMarginalLogLikelihood(self.likelihood, self.gp)
        for i in range(self.training_iter):
            optimizer.zero_grad()
            output = self.gp(self.X)
            loss = -mll(output, self.y)
            loss.backward()
            optimizer.step()

    def predict(self, X):
        self.likelihood.eval()
        self.gp.eval()
        with torch.no_grad(), gpytorch.settings.fast_pred_var():
            pred = self.gp(X)
            return self.likelihood(pred)

Acquisition Function

Khi đã có posterior từ GP, câu hỏi tiếp theo là làm thế nào để chọn được candidate tiềm năng cho ra kết quả (mean) tốt nhất? Cách đơn giản nhất là lựa chọn vị trí maximum của mean, nhưng còn những vùng có uncertainty lớn (standard deviation lớn) cũng rất tiềm năng cho ra kết quả tốt chứ. Acquisition function dựa trên cả 2 yếu tố là cực trị hiện tại và uncertainty của posterior để đưa ra candidate tiềm năng nhất. Một trong những hàm acquisition hay được sử dụng là Expected Improvement (EI) được tính bằng công thuwcs:

$\mathrm{EI}(\mathbf{x})=\left\{\begin{array}{ll} \left(\mu(\mathbf{x})-f\left(\mathbf{x}^{+}\right)-\xi\right) \Phi(Z)+\sigma(\mathbf{x}) \phi(Z) & \text { , nếu } \sigma(\mathbf{x})>0 \\ 0 & \text { , nếu } \sigma(\mathbf{x})=0 \end{array}\right.$

Trong đó $\mathbf{x}^{+}$ là điểm dữ liệu tốt nhất hiện tại; $\mu(\mathbf{x})$ và $\sigma(\mathbf{x})$ lần lượt là mean và variance của $x$ ; $\Phi(Z)$ và $\phi(Z)$ lần lượt là CDF và PDF của phân phối Z:

$Z=\left\{\begin{array}{ll} \frac{\mu(\mathbf{x})-f\left(\mathbf{x}^{+}\right)-\xi}{\sigma(\mathbf{x})} & \text { , nếu } \sigma(\mathbf{x})>0 \\ 0 & \text { , nếu } \sigma(\mathbf{x})=0 \end{array}\right.$

Số hạng $\left(\mu(\mathbf{x})-f\left(\mathbf{x}^{+}\right)-\xi\right) \Phi(Z)$ cho biết "improvement" của $\mathbf{x}$ so với $\mathbf{x}^{+}$ , thể hiện sự exploitation trong khi $\sigma(\mathbf{x}) \phi(Z)$ "khám phá" những nơi có uncertainty (variance) cao, thể hiện sự exploration. Tham số $\xi$ điều khiển trade-off giữa exploration và exploitation. Nhìn công thức có vẻ phức tạp nhưng implement nó lại khá dễ dàng như sau:

def surrogate(model, X):
    distro = model.predict(X)
    return distro.mean, np.sqrt(distro.variance)
 
def acquisition(X, Xsamples, model):
    yhat, _ = surrogate(model, X)
    best = max(yhat)
    mu, std = surrogate(model, Xsamples)
    eps = 0.03
    Z = (mu - best - eps) / std
    ei = (mu - best - eps)*norm.cdf(Z) + std*norm.pdf(Z)
    return ei

Sau khi đã có hàm tính EI cho một điểm x bất kỳ, ta sẽ phải sample rất nhiều x và chọn ra điểm có EI lớn nhất. Tuy hàm EI đã có 2 yếu tố exploration và exploitation, người ta cho rằng nhiều khi nó vẫn hơi "tham lam" nghiêng về expoitation. Vậy nên thay vì chọn điểm EI cao nhất, mình sẽ chọn theo $\epsilon$ -greedy: chọn điểm tốt nhất với xác suất (1- $\epsilon$ ) và chọn một điểm bất kỳ với xác suất $\epsilon$ , và $\epsilon$ sẽ giảm dần theo từng vòng lặp.

def opt_acquisition(X, y, model):
    Xsamples = sample_data(1000)
    scores = acquisition(X, Xsamples, model)
    e = 0.08**(len(X)/ITERS)
    if random(1)[0] > e:
        ix = argmax(scores)
    else:
        ix = np.random.randint(len(scores))
    return Xsamples[ix]

Main loop

Vòng lặp này theo đúng thuật toán:

Train GP regression bằng initial data .
Sử dụng acquisition function chọn candidate (learning rate) tiềm năng nhất.
Evaluate candidate: train lại CNN model bằng candidate đó
Append candidate và giá trị (accuracy) của nó vào tập dữ liệu ban đầu và lặp lại bước 1.

print("Collecting initial observations")
X = sample_lr(2)
y = np.asarray([objective(x) for x in X])
X = torch.DoubleTensor(X)
y = torch.DoubleTensor(y)
model = Regressor(X, y)
model.train()

# for visualization purposes
new_X = []
new_y = []

print("START OPTIMIZATION")
for i in range(ITERS):
    print("Iteration ", i)
    x = opt_acquisition(X, model)
    actual = objective(x)
    est, _ = surrogate(model, torch.DoubleTensor([x]))
    X = np.vstack((X.numpy(), x))
    y = np.hstack((y.numpy(), actual))
    new_X.append(x)
    new_y.append(actual)
    X = torch.tensor(X)
    y = torch.tensor(y)
    model = Regressor(X, y)
    model.train()
ix = np.argmax(y)
print('Best Result:', X[ix, :].numpy(), y[ix].numpy())

Chạy thuật toán (sẽ mất một chút thời gian đó):

Qua 10 vòng lặp, kết quả là giá trị learning rate tốt nhất là 0.012973 với accuracy bằng 0.9823

Visualize posterior

Ta sẽ visualize posterior của GP regression để có cái nhìn trực quan về cách mà BO lựa chọn candidate.

def plot_post(X, y, gp, new_X, new_y):
    pyplot.figure(figsize=(8, 8))
    X_ = np.logspace(-6, 1, 1000)
    y_mean, y_std = surrogate(gp, X_)
    pyplot.xscale('log')
    pyplot.plot(X_, y_mean, 'r', lw=2, zorder=9, label='surrogate function')
    pyplot.fill_between(X_, y_mean - y_std, y_mean + y_std, alpha=0.2, color='k')
    pyplot.scatter(X[:, 0], y, c='r', s=20, zorder=10, edgecolors=(0, 0, 0), label='initial point')
    pyplot.scatter(new_X, new_y, c='g', s=40, zorder=10, edgecolors=(0, 0, 0), label='query point')
    pyplot.legend(loc='upper left')
    pyplot.tight_layout()
    pyplot.xlabel("learning rate")
    pyplot.ylabel("accuracy")
    pyplot.show()

plot_post(X, y, model, np.array(new_X), np.array(new_y))

Và đây là kết qủa. Có thể thấy BO hầu như chọn điểm xung quanh vùng mang lại giá trị accuracy cao nhất nhưng đôi khi nó cũng chọn những vùng khác có uncertainty (variance) cao (vùng màu xám thể hiện variance của posterior).

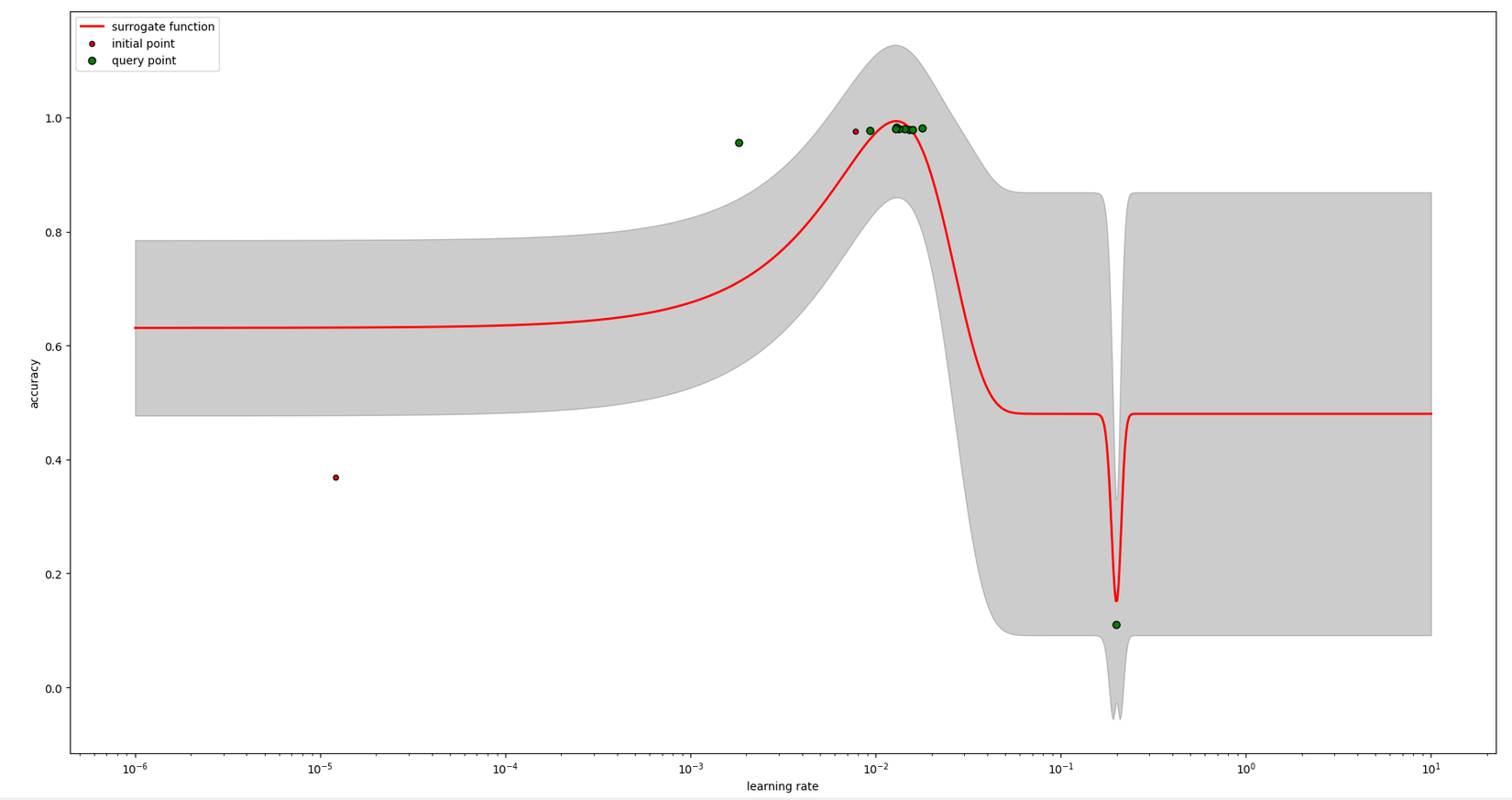
Kết luận

Bài này mình đã giới thiệu và implement với bạn thuật toán tối ưu Bayesian Optimization. Đây là một thuật toán khá hay và hữu dụng trong việc tối ưu, đặc biệt là tối ưu tham số model deep learning. Nếu bài viết có gì sai sót, hãy comment cho mình biết nhé; còn nếu thấy hay thì ngại gì mà không upvote/clip.