Machine learning (Học máy) là một ứng dụng của trí tuệ nhân tạo (AI) cung cấp cho các hệ thống khả năng tự động học hỏi và cải thiện từ kinh nghiệm mà không cần được lập trình rõ ràng.

Một trong những phần khó trong Học máy là đánh giá hiệu suất của Mô hình. Vậy làm cách nào để đo lường sự thành công của một mô hình học máy? Làm thế nào chúng ta biết khi nào nên dừng việc đào tạo và đánh giá và gọi nó là tốt? Và Nên chọn số liệu nào để đánh giá mô hình? Trong Bài viết này, chúng tôi sẽ cố gắng giải đáp những điều này.

Giới thiệu

Một khía cạnh quan trọng của các thước đo đánh giá là khả năng phân biệt giữa các kết quả của mô hình. Đánh giá giúp bạn hiểu thêm về Mô hình của mình. Nó cho biết liệu mô hình của bạn đã ghi nhớ hay đã học. Điều này rất quan trọng nếu mô hình của bạn chỉ ghi nhớ thay vì học, mô hình sẽ chỉ hoạt động tốt đối với dữ liệu đã được huấn luyện và làm cho mô hình không hiệu quả.

Để đảm bảo rằng mô hình của bạn biết được điều quan trọng là sử dụng nhiều số liệu đánh giá để đánh giá mô hình. Bởi vì một mô hình có thể hoạt động tốt khi sử dụng một số liệu đánh giá trong khi hiệu suất có thể giảm đối với một số liệu đánh giá khác. Việc sử dụng nhiều chỉ số đánh giá là rất quan trọng trong việc đảm bảo rằng mô hình của bạn đang hoạt động chính xác và tối ưu.

Tại sao đánh giá là cần thiết cho mô hình thành công?

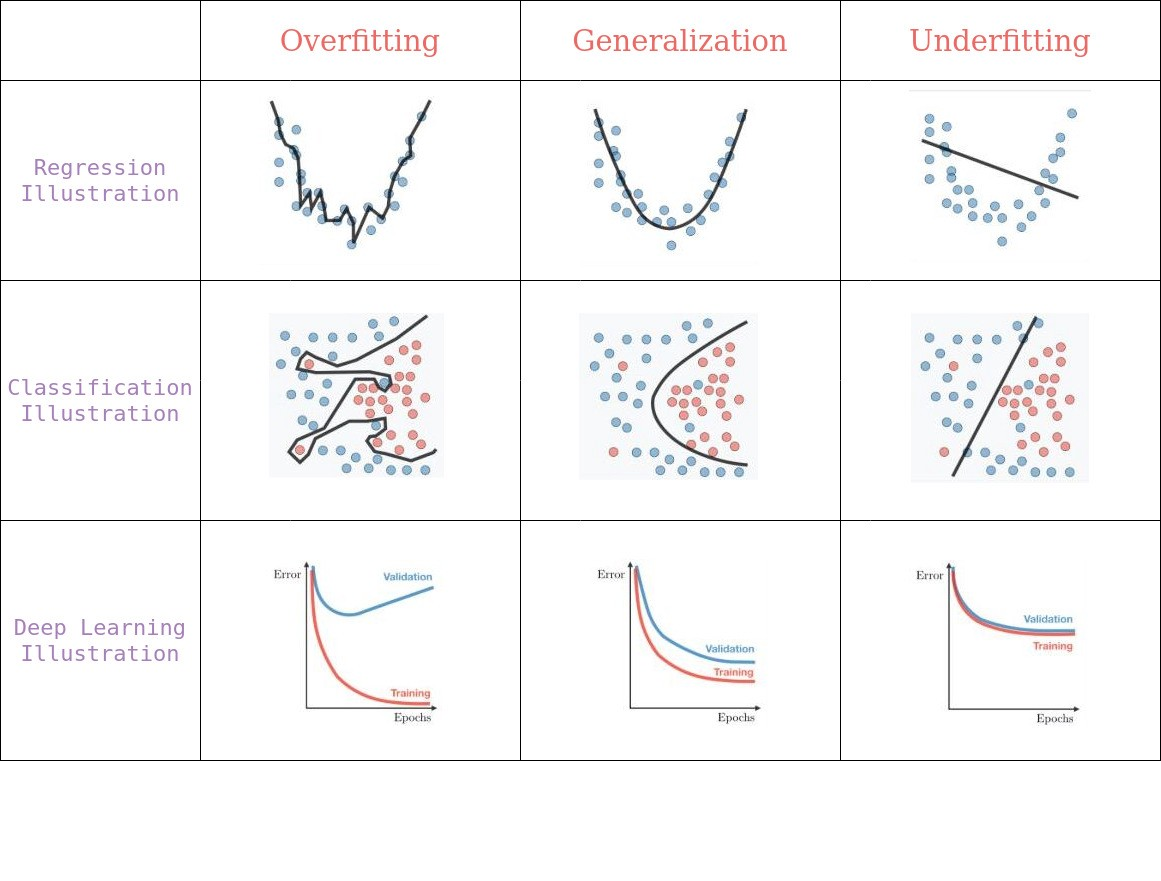
Overfitting và Underfitting là hai nguyên nhân lớn nhất dẫn đến hiệu suất kém của các thuật toán học máy.

Overfitting: Xảy ra khi Mô hình hoạt động tốt đối với một tập hợp dữ liệu cụ thể (Dữ liệu đã biết) và do đó có thể không phù hợp với dữ liệu bổ sung (Dữ liệu không xác định).

Underfitting: Xảy ra khi mô hình không thể nắm bắt đầy đủ cấu trúc cơ bản của dữ liệu.

Tổng quát hóa: đề cập đến mức độ áp dụng của các khái niệm được học bởi một mô hình học máy đối với các ví dụ cụ thể mà mô hình không nhìn thấy khi nó đang học.

Chỉ số đánh giá

Có các số liệu khác nhau cho các nhiệm vụ phân loại, hồi quy, xếp hạng, phân cụm, mô hình hóa chủ đề, v.v. Một số số liệu như sau:

1. Các chỉ số phân loại (accuracy, precision, recall, F1-score, ROC, AUC, …)
2. Chỉ số hồi quy (MSE, MAE)
3. Chỉ số xếp hạng (MRR, DCG, NDCG)
4. Số liệu thống kê (Correlation)
5. Các chỉ số thị giác máy tính (PSNR, SSIM, IoU)
6. Các chỉ số NLP (Perplexity, BLEU score)
7. Các chỉ số liên quan đến Deep Learning Inception score, Frechet Inception distance) Lưu ý: Để hiểu rõ hơn, tôi đã lên kế hoạch tập trung vào các chỉ số Phân loại và Hồi quy trong Bài viết này.

1. Các chỉ số phân loại

Số liệu phân loại

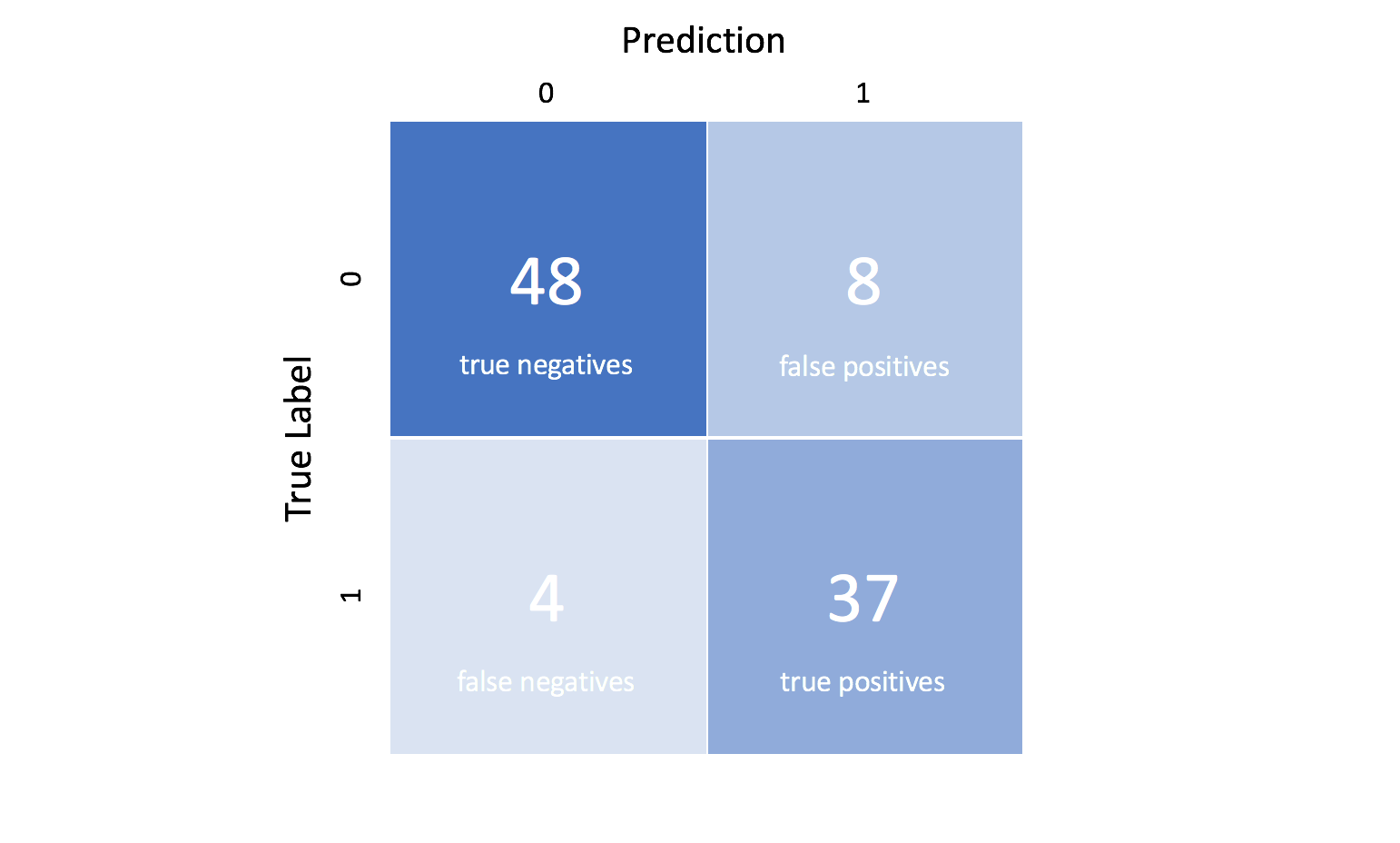
Khi thực hiện các dự đoán phân loại, có bốn loại kết quả có thể xảy ra:

• True positives (TP) là khi bạn dự đoán một quan sát thuộc về một lớp và nó thực sự thuộc về lớp đó.
• True Negative (TN) là khi bạn dự đoán một quan sát không thuộc về một lớp và nó thực sự không thuộc lớp đó.
• False Positive (FP) xảy ra khi bạn dự đoán một quan sát thuộc về một lớp trong khi thực tế thì không.
• False Negative (FN) xảy ra khi bạn dự đoán một quan sát không thuộc về một lớp trong khi thực tế là nó có.

Bốn kết quả này thường được vẽ trên một ma trận nhầm lẫn. Ma trận nhầm lẫn sau đây là một ví dụ cho trường hợp phân loại nhị phân. Bạn sẽ tạo ma trận này sau khi đưa ra dự đoán trên dữ liệu thử nghiệm của mình và sau đó xác định từng dự đoán là một trong bốn kết quả có thể được mô tả ở trên.

Ba thước đo chính được sử dụng để đánh giá một mô hình phân loại là accuracy, precision và recall.

1.1. Accuracy

Accuracy là một thước đo để đánh giá các mô hình phân loại. Về mặt hình thức, accủacy có thể được định nghĩa là số lần dự đoán đúng trên tổng số lần dự đoán.

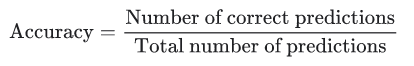
Viết điều này theo True Positive và True Negative: Tỷ lệ phần trăm trường hợp tích cực trong tổng số trường hợp tích cực thực tế . Do đó, mẫu số ( TP + FN) ở đây là số lượng thực tế các trường hợp dương có trong tập dữ liệu.

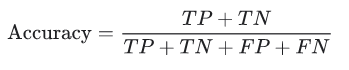
1.2 Precision and Recall

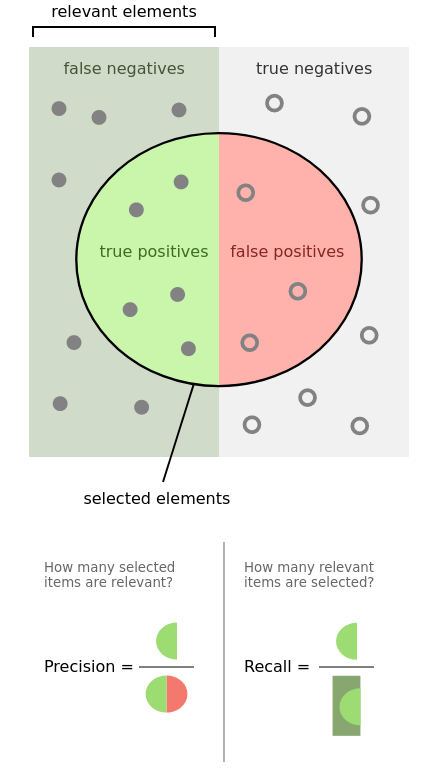
Precsion (còn được gọi là giá trị dự đoán dương) là phần nhỏ của các trường hợp có liên quan trong số các trường hợp được truy xuất, trong khi Recall (còn được gọi là độ nhạy) là phần của các trường hợp có liên quan đã được truy xuất. Do đó, cả độ chính xác và thu hồi đều dựa trên mức độ liên quan.

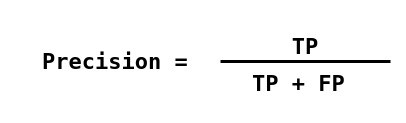
Trong phân loại, Precision là số lượng trường hợp tích cực thực sự (TP) trong tổng số trường hợp được gắn nhãn là thuộc lớp tích cực.

Recall là số lượng các trường hợp dương thực sự trên tổng số các trường hợp thực sự thuộc về lớp tích cực.

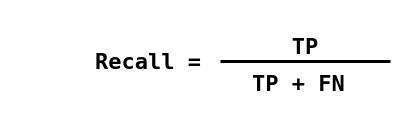
1.3. Điểm F1

Tùy thuộc vào ứng dụng, bạn có thể muốn ưu tiên Recall hoặc Precision cao hơn. Nhưng có nhiều ứng dụng trong đó cả thu hồi và độ chính xác đều quan trọng. Do đó, việc nghĩ ra cách kết hợp cả hai thành một chỉ số duy nhất là điều hoàn toàn tự nhiên.

Cuối cùng, thật tuyệt khi có một con số để đánh giá một mô hình học máy giống như bạn đạt được một điểm duy nhất trong một bài kiểm tra ở trường. Do đó, việc kết hợp các chỉ số đo độ chính xác và độ nhớ lại sẽ rất hợp lý; cách tiếp cận phổ biến để kết hợp các số liệu này được gọi là điểm f.

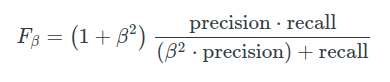
Các β tham số cho phép chúng tôi kiểm soát sự đánh đổi tầm quan trọng giữa độ chính xác và thu hồi. β< 1tập trung nhiều hơn vào độ chính xác trong khi β> 1tập trung nhiều hơn vào việc thu hồi.

Một số liệu phổ biến kết hợp độ chính xác và thu hồi được gọi là điểm F1 , là trung bình hài hòa của độ chính xác và thu hồi được định nghĩa là:

Vì giá trị trung bình hài hòa của một danh sách các số nghiêng nhiều về các phần tử nhỏ nhất của danh sách, nên nó có xu hướng (so với giá trị trung bình cộng) để giảm thiểu tác động của các giá trị ngoại lệ lớn và làm trầm trọng thêm tác động của các giá trị nhỏ.

Một nhược điểm là cả độ chính xác và thu hồi đều có tầm quan trọng như nhau do đó theo ứng dụng của chúng tôi, chúng tôi có thể cần một điểm cao hơn điểm kia và điểm F1 có thể không phải là số liệu chính xác cho nó. Do đó, điểm F1 có trọng số hoặc nhìn thấy đường cong PR hoặc ROC có thể hữu ích.

1.4. Đường cong PR

Đường cong PR chỉ đơn giản là một đồ thị có giá trị Precision trên trục y và giá trị Recall trên trục x. Nói cách khác, đường cong PR chứa TP / (TP + FN) trên trục y và TP / (TP + FP) trên trục x.

Người ta mong muốn rằng thuật toán phải có cả độ chính xác cao và khả năng thu hồi cao. Tuy nhiên, hầu hết các thuật toán học máy thường liên quan đến sự đánh đổi giữa hai thuật toán này.

Một đường cong thu hồi chính xác mẫu cho Mô hình phân loại không có kỹ năng và mô hình hồi quy logistic

1.5. ROC

Đường cong ROC ( đường đặc tính hoạt động của máy thu ) là một đồ thị thể hiện hiệu suất của một mô hình phân loại ở tất cả các ngưỡng phân loại . Đường cong này vẽ hai tham số:

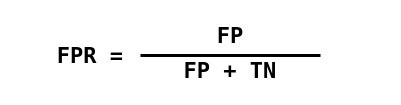
• Tỷ lệ Tích cực Thực sự (Recall)
• Tỷ lệ Tích cực giả (FPR)

Đường cong ROC vẽ biểu đồ TPR so với FPR ở các ngưỡng phân loại khác nhau. Việc hạ thấp ngưỡng phân loại sẽ phân loại nhiều mục hơn là khẳng định, do đó làm tăng cả Khẳng định sai và Khẳng định thật.

Nhiều mô hình phân loại có tính xác suất, tức là chúng dự đoán xác suất của một mẫu là người. Sau đó, họ so sánh xác suất đầu ra đó với một số ngưỡng giới hạn và nếu nó lớn hơn ngưỡng đó, họ dự đoán nhãn của nó là con người, ngược lại là không phải con người. Ví dụ, mô hình của bạn có thể dự đoán các xác suất dưới đây cho 4 hình ảnh mẫu: [0,45, 0,6, 0,7, 0,3] . Sau đó, tùy thuộc vào các giá trị ngưỡng bên dưới, bạn sẽ nhận được các nhãn khác nhau: giới hạn = 0,5: nhãn dự đoán = [0,1,1,0] (ngưỡng mặc định) giới hạn = 0,2: nhãn dự đoán = [1,1,1,1] giới hạn = 0,8: dự đoán- nhãn = [0,0,0,0]

Như bạn có thể thấy bằng cách thay đổi các giá trị ngưỡng, bạn sẽ nhận được các nhãn hoàn toàn khác nhau. Và như bạn có thể tưởng tượng, mỗi tình huống này sẽ dẫn đến độ chính xác và tỷ lệ thu hồi (cũng như TPR, FPR) khác nhau.

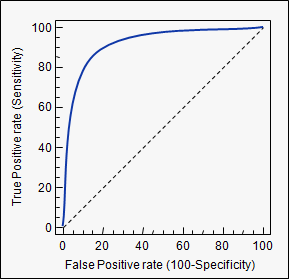
Để tính toán các điểm trong đường cong ROC, bạn có thể đánh giá mô hình hồi quy logistic nhiều lần với các ngưỡng phân loại khác nhau, nhưng điều này sẽ không hiệu quả. May mắn thay, có một thuật toán hiệu quả, dựa trên phân loại có thể cung cấp thông tin này, được gọi là AUC.

1.6. AUC

Diện tích dưới đường cong (AUC), là thước đo tổng hợp hiệu suất của bộ phân loại nhị phân trên tất cả các giá trị ngưỡng có thể có (và do đó nó là ngưỡng bất biến ) . Nghĩa là, AUC đo toàn bộ diện tích hai chiều bên dưới toàn bộ đường cong ROC.

Vì AUC là một phần của diện tích hình vuông đơn vị, nên giá trị của nó sẽ luôn nằm trong khoảng từ 0 đến 1,0. Tuy nhiên, vì đoán ngẫu nhiên tạo ra đường chéo giữa (0, 0) và (1, 1), có diện tích 0,5, không có bộ phân loại thực tế nào có AUC nhỏ hơn 0,5

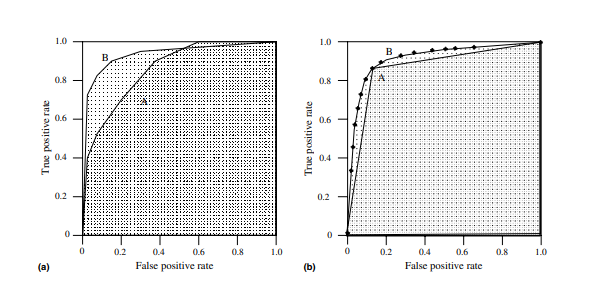
AUC được mong muốn vì hai lý do sau:

• AUC là bất biến quy mô . Nó đo lường mức độ xếp hạng của các dự đoán thay vì giá trị tuyệt đối của chúng.
• AUC là một phân loại-ngưỡng-bất biến . Nó đo lường chất lượng của các dự đoán của mô hình bất kể ngưỡng phân loại nào được chọn.

2. Chỉ số hồi quy

Các số liệu đánh giá cho mô hình hồi quy khá khác so với các số liệu ở trên mà chúng ta đã thảo luận cho các mô hình phân loại bởi vì chúng tôi hiện đang dự đoán trong một phạm vi liên tục thay vì một số lớp rời rạc. Nếu mô hình hồi quy của bạn dự đoán giá một ngôi nhà là 400 nghìn đô la và nó được bán với giá 405 nghìn đô la thì đó là một dự đoán khá tốt. Tuy nhiên, trong các ví dụ phân loại, chúng tôi chỉ quan tâm đến việc một dự đoán đúng hay sai, không có khả năng nói một dự đoán là "khá tốt". Do đó, chúng tôi có một bộ số liệu đánh giá khác nhau cho các mô hình hồi quy.

2.1. Mean Squared Error

Mean Squared Error (MSE) có lẽ là số liệu phổ biến nhất được sử dụng cho các bài toán hồi quy. Về cơ bản, nó tìm thấy sai số bình phương trung bình giữa các giá trị được dự đoán và thực tế. MSE là thước đo chất lượng của một công cụ ước tính - nó luôn không âm và các giá trị càng gần 0 càng tốt. trong đó n là số điểm dữ liệu, yᵢ là giá trị quan sát và ŷ ᵢ là giá trị dự đoán.

Trong phân tích hồi quy, vẽ biểu đồ là một cách tự nhiên hơn để xem xu hướng chung của toàn bộ dữ liệu. Đơn giản MSE cho bạn biết mức độ gần của đường hồi quy với một tập hợp các điểm. Nó thực hiện điều này bằng cách lấy khoảng cách từ các điểm đến đường hồi quy (những khoảng cách này là “sai số”) và bình phương chúng. Bình phương là rất quan trọng để giảm độ phức tạp với các dấu hiệu tiêu cực. Nó cũng tạo ra nhiều trọng lượng hơn cho sự khác biệt lớn hơn.

Để giảm thiểu MSE, mô hình có thể chính xác hơn, có nghĩa là mô hình gần với dữ liệu thực tế hơn. Một ví dụ về hồi quy tuyến tính sử dụng phương pháp này là - phương pháp bình phương nhỏ nhất đánh giá sự phù hợp của mô hình hồi quy tuyến tính với tập dữ liệu hai biến, nhưng giới hạn của nó liên quan đến phân phối dữ liệu đã biết.

MSE càng thấp thì dự báo càng tốt.

2.2. Mean Absolute Error

Mean Absolute Error (MAE) đo độ lớn trung bình của các lỗi trong một tập hợp các dự đoán mà không cần xem xét hướng của chúng. Đó là giá trị trung bình trên mẫu thử nghiệm về sự khác biệt tuyệt đối giữa dự đoán và quan sát thực tế, trong đó tất cả các khác biệt riêng lẻ có trọng số bằng nhau. trong đó n là số điểm dữ liệu, xᵢ là giá trị thực và yᵢ là giá trị dự đoán.

Có thể diễn đạt MAE là tổng hòa của hai thành phần: Bất đồng về số lượng và Bất đồng về phân bổ.

MAE được biết đến là mạnh mẽ hơn đối với các yếu tố ngoại lai so với MSE. Lý do chính là trong MSE bằng cách bình phương các sai số, các giá trị ngoại lai (thường có sai số cao hơn các mẫu khác) được chú ý nhiều hơn và chiếm ưu thế trong sai số cuối cùng và tác động đến các tham số của mô hình.

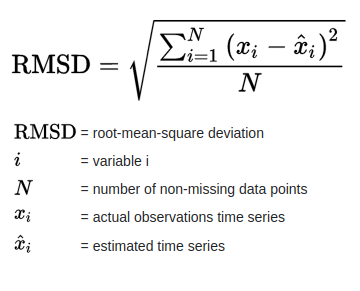
2.3. Root Mean Square Error

Root Mean Square Error (RMSE) hoặc Root Mean Square Deviation (RMSD) là căn bậc hai của mức trung bình của các sai số bình phương. RMSE là độ lệch chuẩn của các phần dư (sai số dự đoán).

Phần dư là thước đo khoảng cách từ các điểm dữ liệu đường hồi quy; RMSE là thước đo mức độ dàn trải của những phần dư này, nói cách khác, nó cho bạn biết mức độ tập trung của dữ liệu xung quanh đường phù hợp nhất.

Ảnh hưởng của mỗi lỗi đối với RMSE tỷ lệ với kích thước của lỗi bình phương; do đó các sai số lớn hơn có ảnh hưởng lớn đến RMSE một cách không cân xứng. Do đó, RMSE nhạy cảm với các yếu tố ngoại lai. Sai số bình phương trung bình gốc thường được sử dụng trong khí hậu học, dự báo và phân tích hồi quy để xác minh kết quả thực nghiệm.

Khi các quan sát và dự báo chuẩn hóa được sử dụng làm đầu vào RMSE, có mối quan hệ trực tiếp với hệ số tương quan . Ví dụ, nếu hệ số tương quan là 1, RMSE sẽ bằng 0, bởi vì tất cả các điểm nằm trên đường hồi quy (và do đó không có sai số).

RMSE luôn không âm và giá trị 0 (hầu như không bao giờ đạt được trong thực tế) sẽ chỉ ra sự phù hợp hoàn hảo với dữ liệu. Nói chung, RMSD thấp hơn sẽ tốt hơn RMSD cao hơn.

Kết luận

Trong bài viết này, chúng tôi đã thảo luận về lý do tại sao chúng tôi đánh giá các mô hình Học máy và các kỹ thuật để đánh giá. Một mô hình được đánh giá để xác nhận rằng nó đang đưa ra những dự đoán tốt. Các kỹ thuật đánh giá phụ thuộc vào loại vấn đề mà mô hình được đào tạo để giải quyết và loại thuật toán. Trong một thời gian dài, accuracy là thước đo duy nhất mà tôi sử dụng, đó thực sự là một lựa chọn mơ hồ. Tôi hy vọng bài viết này sẽ hữu ích cho bạn. Cảm ơn đã đọc bài viết và mong nhận được sự góp ý của mọi người.