Cấu trúc dữ liệu và giải thuật - Danh sách liên kết.

Danh sách liên kết là gì

Danh sách liên kết là 1 cấu trúc dữ liệu có kiểu tuần tự, mỗi phần tử trong danh sách liên kết có chứa thông tin, qua đó ta có thể truy cập tới phần tử này.

Các loại danh sách liên kết

• Danh sách liên kết đơn.
• Danh sách liên kết vòng.
• Danh sách liên kết kép.

Danh sách liên kết đơn

Nút (node) : bao gồm 2 thành phần

• Data: chứa dữ liệu
• Next: chứa kết nối đến node tiếp theo

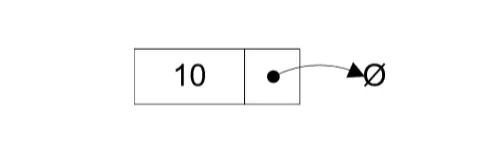
Trong Xcode ta tạo 1 class tên là Node: để node có thể nhận được nhiều kiểu giá trị khác nhau ta dùng kiểu generics cho data.

class Node<T> {
    var data: T?
    var next: Node?
}

1 danh sách liên kết hoàn chỉnh sẽ có dạng thế này:

Tiếp theo trong Xcode ta tạo 1 class LinkedList:

public class LinkedList<T: Equatable> {

}

Danh sách liên kết bắt đầu từ 1 node, node đó gọi là head:

private var head: Node<T> = Node<T>()

Các thao tác cơ bản trên danh sách liên kết đơn

Thêm 1 nút vào cuối danh sách

Để thêm 1 node mới vào cuối danh sách ta làm theo các bước như sau

• Bắt đầu duyệt từ đầu danh sách.
• Lần lượt dịch chuyển theo thứ tự các node cho đến khi đến cuối danh sách.
• Gán link node cuối vào node muốn thêm vào, link node muốn thêm vào sẽ trỏ vào nil. Ta viết hàm thêm vào file LinkedList như sau:

func addLink(data: T) {

        if (head.data == nil) {
            head.data = data
            return
        }

        // Lay node head
        var current: Node? =  head

        while (current != nil) {
            // Kiem tra xem node hien tai co tro den nil ko
            // Neu node hien tai tro den nil tuc la da o cuoi danh sach
            if current?.next == nil {

                let newNode: Node = Node<T>()

                newNode.data = data
                current!.next = newNode
                break
            }
            // Neu chua phai node cuoi danh sach lay node tiep theo de kiem tra
            else {
                current = current?.next
            }
        }
    }

Thêm 1 node vào vị trí index trong danh sách

• Bắt đầu duyệt từ đầu danh sách.
• Lần lượt dịch chuyển đến các node, kiểm tra current index có bằng index muốn thêm ko
• Nếu bằng thì gán node trước đó trỏ vào node muốn thêm, node muốn thêm trỏ vào node hiện tại.

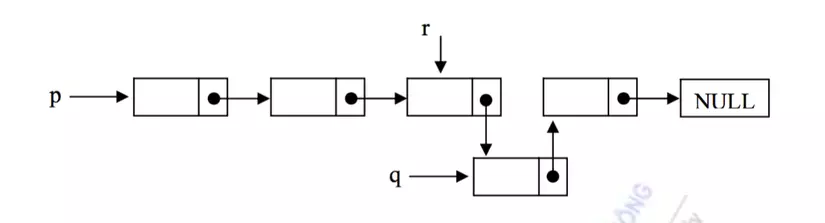
Ta thêm đoạn code sau vào file LinkedList:

// Them 1 node vao vi tri index trong danh sach
    func addLinkAtIndex(data: T, index: Int) {

        //Kiem tra xem danh do co node head ko
        if (head.data == nil) {
            head.data = data
            return
        }

        // Bat dau duyet tu node head
        var currentNode: Node<T>? = head
        var previousNode: Node<T>?
        var currentIndex: Int = 0

        // Neu node hien tai khong tro den nil tuc la chua den cuoi danh sach
        while (currentNode != nil) {

            // kiem tra index
            if (currentIndex == index) {

                // tao node moi
                let newNode: Node = Node<T>()
                newNode.data = data

                // tro node moi link den node hien tai
                newNode.next = currentNode

                // kiem tra xe previous node co ton tai ko
                if let previousNode = previousNode {
                    previousNode.next = newNode
                }

                // them node moi vao vi tri dau tien gan lai head vao node moi
                if (index == 0) {
                    head = newNode
                }

                break
            }

            // luu lai node truoc do
            previousNode = currentNode

            // tro node hien tai den node ke tiep
            currentNode = currentNode?.next

            // tang index len
            currentIndex += 1
        }
    }

Xoá node ở cuối danh sách

• Bắt đầu duyệt từ đầu danh sách.
• Lần lượt dịch chuyển đến các node, kiểm tra node.next có trỏ tới nil.
• Nếu node.next trỏ tới nil thì dịch chuyển next của node trước đó đến nil.

Ta thêm đoạn code sau trong LinkedList:

func removeLastNode() {
        // Kiem tra xem danh do co node head ko
        if head.data == nil {
            return
        }

        var currentNode: Node<T>? = head

        // duyet mang
        while currentNode != nil {
            // lay node tiep theo cua current node
            let nextNode = currentNode?.next

            // kiem tra xem node tiep theo cua nextNode co nil ko, neu cos nextNode la node cuoi danh sach
            if nextNode?.next == nil {
                currentNode?.next = nil
                break
            }
            else {
                currentNode = nextNode
            }
        }
    }

Xoá 1 node tại vị trí index

• Duyệt từ đầu danh sách.
• Giả sử ta có node q tại vị trí index muốn xoá, ta có node trước đó là nút r.
• Cho next của node r trỏ vào nút tiếp theo của node q.

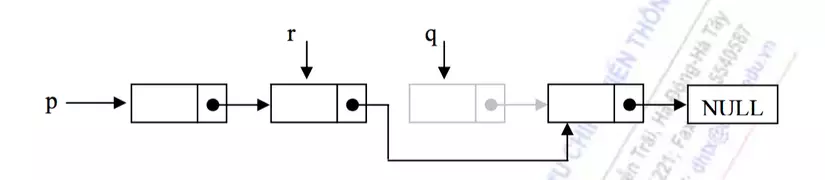
Ta thêm đoạn code sau trong LinkedList:

func removeLinkAtIndex(index: Int) {

        // Kiem tra xem danh do co node head ko
        if head.data == nil {
            return
        }

        var currentNode: Node<T>? =  head
        var previousNode: Node<T>?
        var currentIndex = 0

        // neu xoa node dau danh sach thi gan node tiep theo ve node dau danh sach
        if (index == 0) {
            currentNode = currentNode?.next
            head = currentNode!
            return
        }

        // duyet mang
        while (currentNode != nil) {

            // tim dc dung index
            if (currentIndex == index) {

                // tro next cua node truoc do vao next node hien tai
                previousNode!.next = currentNode?.next
                currentNode = nil
                break
            }

            // tro toi node tiep theo tang index
            previousNode = currentNode
            currentNode = currentNode?.next
            currentIndex += 1

        }
    }

Duyệt toàn bộ danh sách

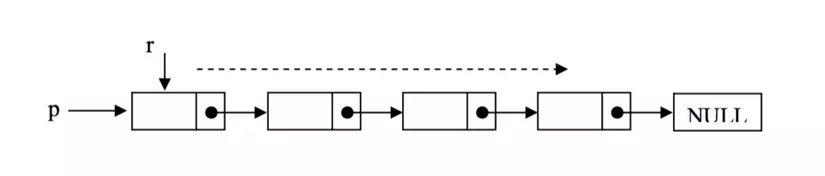
• Thao tát duyệt cho phép duyệt qua các phần tử trong danh sách.
• Để thực hiện ta bắt đầu duyệt từ 1 node r từ đầu danh sách.
• Dịch chuyển node r lần lượt theo các node tiếp theo.
• Trong quá trình duyệt ta có thể lấy đc thông tin của node đó.

func printAllNode() {
        // Lấy node head
        var current: Node! = head

        // Duyệt mảng

        while current != nil {
            print("Node : \(current.data!)")
            current = current.next
        }

    }

Kiểm tra thuật toán có chạy đúng không

• Code thực hiện có trong file demo còn đây là kết quả test:

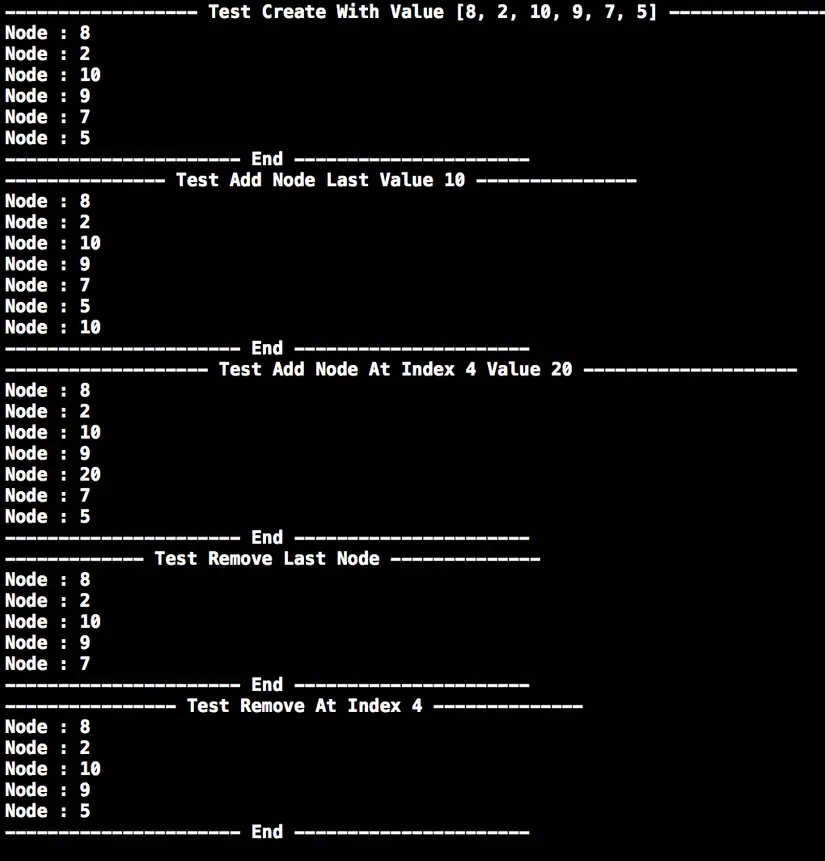
Danh sách liên kết vòng

• Tương tự như danh sách liên kết đơn nhưng node cuối danh sách thay vì trỏ ra nil thì nó sẽ trỏ vào head (node đầu danh sách)

• Ưu điểm của danh sách liên kết vòng đó là bất kỳ node nào cũng có thể coi là đầu danh sách(head), có nghĩa là từ 1 node bất kỳ ta đều có thể duyệt qua toàn bộ các phần tử của danh sách mà không cần trở về node đầu tiên danh sách.

Danh sách liên kết kép

• Trong danh sách liên kết đơn, mỗi node chỉ có 1 liên kết tới node kết tiếp. Điều này có nghĩa danh sách liên kết đơn chỉ cho phép duyệt theo 1 chiều trong khi thao tát duyệt chiều ngược lại cũng rất cần thiết.
• Để giải quyết vấn đề này tại mỗi node ta tạo 2 liên kết: 1 liên kết trỏ tới node đứng trước, 1 liên kết trỏ tới node đứng sau.

Trong class Node ta thêm 1 thuộc tính previous

class Node<T> {
    var data: T?
    var next: Node?

    // thuộc tính chỉ dùng với danh sách liên kết kép
    var previous: Node?
}

Tài liệu tham khảo

• Cấu trúc dữ liệu và giải thuật - Học viên bưu chính viễn thông.
• http://www.tutorialspoint.com/data_structures_algorithms/linked_lists_algorithm.htm

Demo

https://github.com/pqhuy87it/MonthlyReport/tree/master/LinkedList