I. Autocorrect là gì?

Autocorrect (Tự động sửa ) là việc điện thoại, máy tính bảng và máy tính tự sửa chữa những từ sai chính tả khi người dùng đang gõ văn bản hoặc nhắn tin, .v.v. Ví dụ:

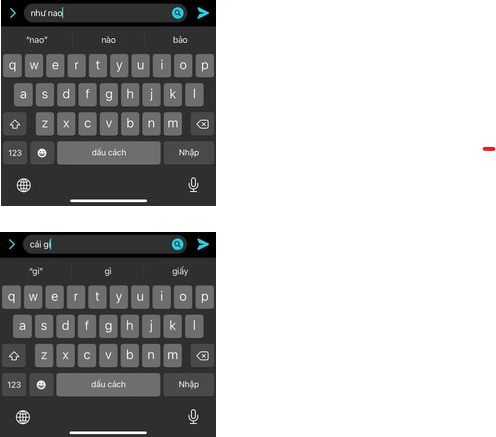
Như minh họa ở trên, từ "nao" đã được gợi ý thành "nào" hoặc "bảo", còn từ "gi" được gợi ý thành "gì" hoặc "giấy".

II. Các bước thực hiện

Để triển khai autocorrect, chúng ta cần thực hiện các bước sau:

• Bước 1: Xác định từ sai chính tả.
• Bước 2: Tìm các từ bằng Minimum edit distance(đây có thể là các từ ngẫu nhiên).
• Bước 3: Chọn ra các từ khả năng thay thế từ sai chính tả ban đầu.
• Bước 4: Tính xác suất của các từ vừa tìm được trong bước 3: (chọn từ có nhiều khả năng xảy ra nhất trong ngữ cảnh đó).

1. Xác định từ sai chính tả

Khi xác định từ sai chính tả, chúng ta có thể kiểm tra xem nó có trong từ điển hay không. Nếu không tìm thấy nó, thì có lẽ đó là lỗi đánh máy. Còn có những cách làm khác chính xác hơn là việc chỉ xét xem nó có thuộc từ điển hay không ví dụ như quan sát các từ bên cách của từ bị nghi ngờ là sai chính tả này.

2. Tìm các từ gần giống bằng Minimum edit distance

Đây là bước thú vị nhất trong autocorrect. Chúng ta sẽ tìm ra các từ gần giống với từ sai chính tả này nhờ thuật toán Minimum edit distance(lưu ý các từ này có thể là các từ ngẫu nhiên không nhất thiết phải trong từ điển).

Thuật toán Minimum edit distance

Thuật toán này có rất nhiều ứng dụng trong thực tế. Ví dụ như:

• Minimum edit distance cho phép đánh giá độ giống/khác nhau giữa hai chuỗi từ.
• Tìm số lần chỉnh sửa tối thiểu giữa hai từ.
• Thực hiện sửa lỗi chính tả, tính tương tự tài liệu, dịch máy, giải trình tự DNA, v.v.

Trong thuật toán này, có 3 loại chỉnh sửa ta cần ghi nhớ đó là insert(chèn), delete(xóa) và replace(thay thế).

• Insert(1 chữ cái duy nhất): "to" -> "top", "two", ..
• Delete(1 chữ cái duy nhất):" "hat" -> "ha", "ht", ..
• Replace(1 chữ cái duy nhất): "jaw" -> "jar", "paw", ..

Ta có edit cost như sau:

• Insert cost: 1
• Delete cost: 1
• Replace cost: 2

Sau đây là một ví dụ:

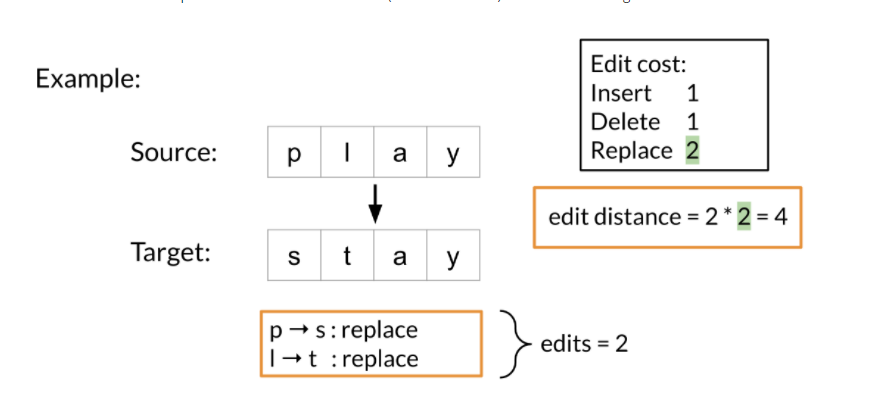
Lưu ý rằng khi các chuỗi của bạn lớn hơn, việc tính toán khoảng cách chỉnh sửa tối thiểu sẽ khó hơn nhiều. Do đó chúng ta sẽ sử dụng dạng bảng để mô tả, Levenshtein distance và thuật toán quy hoạch động để tính toán khoảng cách một cách hiệu quả hơn.

Giả sử ta có từ gốc là: "Play", từ đích là: "Stay". Xem hình minh họa sau đây:

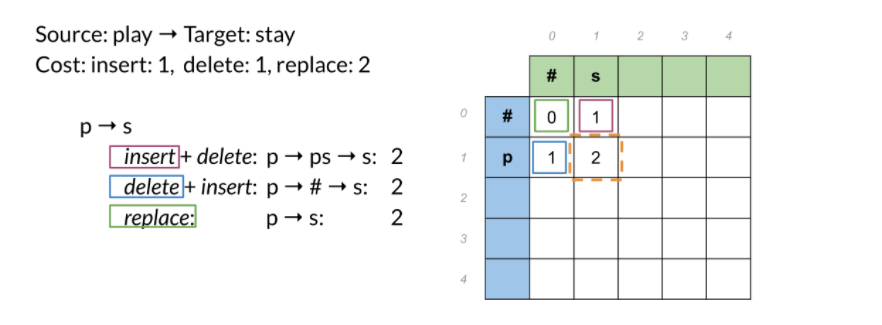
$i$ là hàng và minh họa cho chữ cái thứ $i$ của từ gốc.

$j$ là cột và minh họa cho chữ cái thứ $j$ của từ đích.

Các ô trong bảng có dạng $D[i, j]$, nó biểu thị cost của $i$ chữ cái đầu của từ gốc và $j$ chữ cái đầu của từ đích.

Ta có $D[0, 0] = 0$, vì # -> # ta không cần bất kì chỉnh sửa nào.'

$D[1, 0] = 0$ vì p -> # ta đã thực hiện delete("p") và cũng tương tự như vậy ta có $D[0, 1] = 1$

Nhưng khi đến $D[1,1]$ lại khác vì ta có 3 cách lựa chọn đường đi:

• insert("s") rồi delete("p"), ta nhận được cost = 2
• delete("p") rồi insert("s"), ta nhận được cost = 2
• replace("p" -> "s") ta nhận được cost = 2

Vì giải thuật luôn luôn cần những cách tối ưu hóa tốt nhất sao cho cost là tối thiểu. Ta thấy $D[1,1]$ có 3 đường đi đều cho cost bằng 2, nên $D[1,1]$ = 2. Nhưng trong cách trường hợp mà cost của 3 đường đi này là khác nhau, ta phải chọn đường đi có cost là nhỏ nhất. Vì vậy, ta sẽ áp dụng quy hoạch động cho bài toán này.(Quy hoạch động là một thuật toán có rất nhiều ứng dụng trong khoa học máy tính, mọi người có thể đọc tài về quy hoạch động ở phần tài liệu tham khảo bên dưới)

Ta có 3 đường đi cụ thể cho mọi ô trong bảng trên như sau:

• $D[i, j] = D[i-1, j] + cost_{del}$, với $i > 0$, $cost_{del} = 1$
• $D[i, j] = D[i, j-1] + cost_{ins}$ , với $j > 0$, $cost_{ins} = 1$
• $D[i, j] = D[i-1, j-1] + cost_{rep}$, với $j > 0$, $i > 0$, $cost_{rep} = 2$ hoặc $cost_{rep} = 0$ tùy theo bạn có muốn thay đổi chữ hay không.

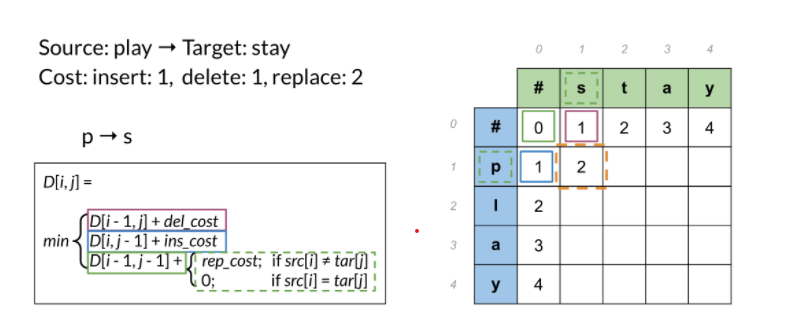
Tại mỗi bước, ta kiểm tra ba con đường có thể đến và chọn một con đường ít tốn kém nhất. Sau khi hoàn tất, ta sẽ nhận được:

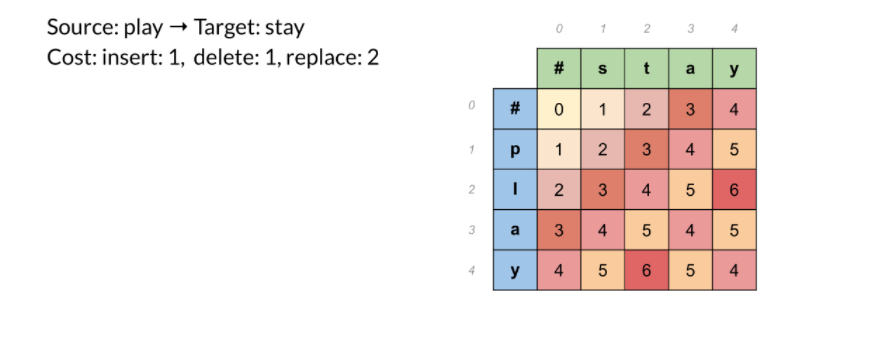
Tóm lại, ta đã thấy levenshtein distance xác định cost cho mỗi ô trên và xác định được cost nhỏ nhất cho việc chỉnh sửa từ. Nếu cần xây dựng lại đường dẫn cách ta đi từ chuỗi này sang chuỗi khác, ta có thể sử dụng backtrace(Tài liệu về backtrace mình để ở phần tài liệu tham khảo). Đối với autocorrect trong thực tế, cost thường giao động từ 1 -> 3

3. Chọn ra các từ khả năng thay thế từ sai chính tả ban đầu

Trong bước này, ta muốn lấy tất cả các từ đã tạo ở trên và sau đó chỉ giữ lại những từ có nghĩa trong thực tế và ta có thể tìm thấy trong từ điển.

4. Tính xác suất của các từ

Ta sẽ tính xác suất của các từ vừa tìm được trong bước 3 để xem từ nào phù hợp trong ngữ cảnh hiện tại nhất.

Việc tính xác suất này thực tế tương đối phức tạp vì từ hiện tại còn liên quan đến các từ phía trước. Nhưng ở đây, để đơn giản, mình sẽ bỏ qua các từ phía trước.

Ví dụ, ta có câu: "I am learnin".

Ở đây từ "learnin" là từ đã bị viết sai và ta cần chỉnh sửa lại nó.

Sau khi thực hiện bước 3, ta nhận được các từ xuất hiện trong từ điển và có nghĩa là: "learning", "learn", "learned".

Ta tính xác suất của các từ "learning", "learn", và "learned" bằng công thức sau:

$$P(word) = \frac{C(word)}{V}$$

$C(word)$: số lần xuất hiện của từ cần tính xác suất trong corpus

$V$: kích thước của corpus

III. Kết luận

Như vậy, mình đã trình bày xong Autocorrect theo một hướng đi tương đối dễ hiểu. Hi vọng bài viết này có thể giúp các bạn nắm được phần nào cách hoạt động của Autocorrect trên những chiếc smart-phone hoặc máy tính bảng.

Tài liệu tham khảo

https://www.giaithuatlaptrinh.com/?p=66 - đây là một bài viết hay về quy hoạch động.

https://www.geeksforgeeks.org/backtracking-algorithms/ - thuật toán quy lui(backtrace hay backtracking)