fairytypean @thangpd3160

Đã đăng vào thg 10 10, 2021 4:58 SA 15 phút đọc

670

Writeup FUSEC 2021 (Season 4)

Bài đăng này đã không được cập nhật trong 3 năm

CRYPTO

1. CRY301 (1000 pts)

Một bài crypto giải bằng kiến thức toán học và tư duy về code. Full source code đề bài xem tại đây

Bài này yêu cầu mình tìm được số xban đầu từ kết quả của 2 hàm easyone(x) và alittlebitharderone(x).

a. Phân tích hàm `easyone(x)`

Nhìn sơ qua hàm easyone(x), có 3 phép biến đổi chính được lặp đi lặp lại 3 lần

Phép xor với left shift bit của chính nó
Phép nhân
Phép & với 0xffffffffffffffffffffffffffffffff.

def easyone(x):
    assert(x < 2 ** 128)
    x ^= x >> (64 + 19)
    x *= 0xd3856e824d9c8a26aef65c0fe1cc96db #281159923981539500379670095774511568603
    x &= 0xffffffffffffffffffffffffffffffff
    x ^= x >> (64 + 3)
    x *= 0xe44035c8f8387dc11dd3dd67097007cb #303397380928069120521467215513016862667
    x &= 0xffffffffffffffffffffffffffffffff
    x ^= x >> (64 + 20)
    x *= 0xc9f54782b4f17cb68ecf11d7b378e445 #268448390289851351177030176676964262981
    x &= 0xffffffffffffffffffffffffffffffff
    x ^= x >> (64 + 2)
    return x

Như vậy, có 2 bài toán đặt ra cần giải quyết:

Tìm x biết $a*x = b \pmod n$ với $a$ , $b$ , $n$ đã biết.
Khôi phục lại kết quả phép xor. Tìm x có $a \oplus x = b$ với $a$ , $b$ đã biết. Khá đơn giản với $x=a \oplus b$ .

Cùng đi sâu hơn chút vào từng bài toán 1 nhé

Bài toán 1: Tìm x biết $a*x = b \pmod n$ với $a$ , $b$ , $n$ đã biết.

Đây là bài toán cơ bản cơ bản về inverse mod (modular inverse) trong finite field (trường hữu hạn). Đơn giản, mình có thể tìm $x$ bằng cách $x = a^{-1} * b \pmod n$ , trong đó $a^{-1} \pmod n$ là giá trị inverse modulo của a trong finite field $\bmod (n)$ .

Chi tiết cách tìm inverse mod bằng toán học với extended euclidean algorithm có thể xem tại đây. Lúc code giải thì mình dùng luôn hàm invert(a, n) trong thư viện gmpy2 của python để tìm $a^{-1} \pmod n$

Mình chuyển 1 đoạn code sang dạng bài toán gốc để dễ hình dung. Cụ thể, đoạn code dưới đây biểu diễn dưới dạng toán học sẽ là $x * 281159923981539500379670095774511568603 = b \pmod n$ với $b$ có thể thu được từ việc dịch lại phép xor (sẽ nói ở bài toán 2).

Lưu ý: x &= 0xfffffffffffffffffffffffffffffffftương đương với x %= 0xffffffffffffffffffffffffffffffff, hay x %= 2**128

x *= 0xd3856e824d9c8a26aef65c0fe1cc96db #281159923981539500379670095774511568603
x &= 0xffffffffffffffffffffffffffffffff

Như vậy, ta có thể dễ dàng tìm $x$ với $x = b*281159923981539500379670095774511568603^{-1} \pmod {2^{128}}$ .

x *= gmpy2.invert(268448390289851351177030176676964262981, 2**128)
x &= 0xffffffffffffffffffffffffffffffff

Vấn đề là để hoàn thiện quá trình giải thì mình cần tìm $b$ , nghĩa là cần phải giải quyết bài toán số 2. Ngay sau đây

Bài toán 2: Khôi phục lại kết quả phép xor

Để giải quyết phần xor này, chúng ta cần phải lưu tâm x sau khi bitshift thì còn những bit nào còn giữ nguyên, bit nào dịch chuyển để thực hiện xor.

x ^= x >> (64 + 2)

Để dễ hình dung, bạn có thể nhìn hình mô phỏng trước và sau khi leftshift dưới đây. Bit màu xanh là những bit còn giữ nguyên sau khi leftshift. Bit màu vàng là bit màu xanh được chuyển ra sau khi leftshift. Bit màu đỏ là những bit có thể bị thay đổi sau bitshift (và cũng là bit thực sự tham gia xor)

Mô phỏng trước và sau khi leftshift. Bit màu xanh là những bit còn giữ nguyên sau khi leftshift. Bit màu vàng là bit màu xanh được chuyển ra sau khi leftshift. Bit màu đỏ là những bit có thể bị thay đổi sau bitshift (và cũng là bit thực sự tham gia xor).

Dễ dàng nhận thấy, phần bit dùng để xor với giá trị x ban đầu vẫn giữ nguyên sau khi xor $\longrightarrow$ Như vậy mình có thể dễ dàng khôi phục phần bit dùng để xor bằng cách leftshift lại giá trị sau khi xor bằng đúng một khoảng dùng để xor trước đó (tức leftshift (64+2) đơn vị trong trường hợp trên).

x ^= x >> (64 + 2)

Kết luận trên đúng với tất cả trường mà x được leftshift ít nhất 64 đơn vị.

Vậy là mình đã giải quyết xong cả 2 bài toán trên! Cuối cùng mình có đoạn code để lấy giá trị x từ hàm easyone(x) như sau:

def solveeasyone(x):
    x ^= x >> (64 + 2)
    x *= gmpy2.invert(268448390289851351177030176676964262981, 2**128)
    x &= 0xffffffffffffffffffffffffffffffff
    x ^= x >> (64 + 20)
    x *= gmpy2.invert(303397380928069120521467215513016862667, 2**128)
    x &= 0xffffffffffffffffffffffffffffffff
    x ^= x >> (64 + 3)
    x *= gmpy2.invert(281159923981539500379670095774511568603, 2**128)
    x &= 0xffffffffffffffffffffffffffffffff
    x ^= x >> (64 + 19)
    return int(x)

Tada, first round~~

b. Phân tích hàm `alittlebitharderone(x)`

Giải quyết hàm này cũng cần giải quyết 2 bài toán như hàm easyone(x). Bài toán 1 về tìm inverse mod hoàn toàn giống hệt. Cái khó hơn nằm ở Bài toán 2, do mình không thể ngay lập tức khôi phụ được bit dùng trong phép xor trước đó từ kết quả thu được.

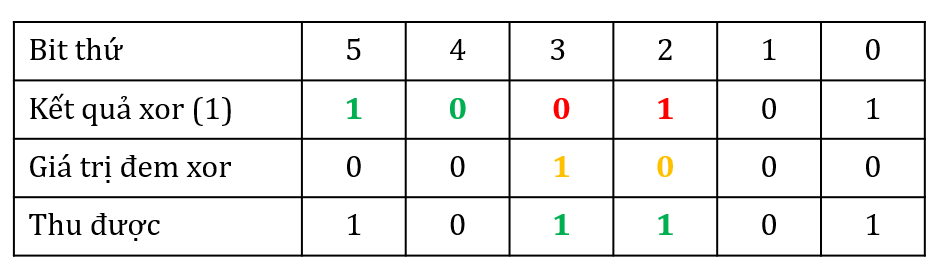
Tuy nhiên, điều đáng mừng là nguyên lý cách làm vẫn thế. Chúng ta cũng sẽ dùng những bit còn nguyên, để khôi phục lại những bit gốc, rồi lân la dần dần để khôi phục toàn bộ bit gốc đó. Mình mô phỏng với 1 bài toán nhỏ với 1 chuỗi 6 bit với độ leftshift bằng 2 như sau: Với trường hợp như trên, mình khôi phục lại giá trị ban đầu của x bằng cách đi qua từng bước như sau đây (Mô tả bằng hình ảnh cho dễ hiểu nhé)

Xor 2 bit đầu (2 bit còn giữ nguyên sau khi xor) với 2 bit liền kều sau nó. Những bit còn lại giữ nguyên. Như vậy, mình đã khôi phục lại được bit số 3 và bit số 2
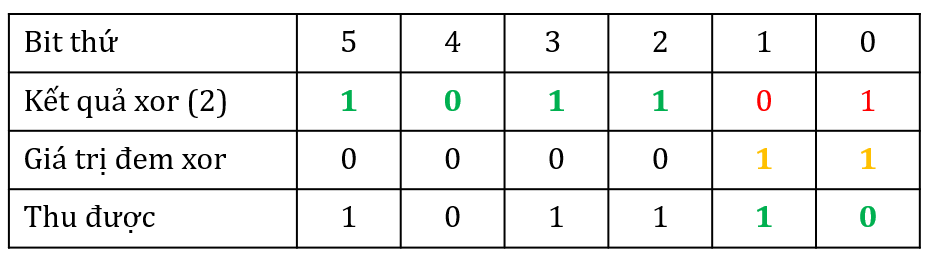
Xor tiếp 2 bit vừa thu được (bit số 3 và 2) với 2 bit liền kề sau nó để khôi phục tiếp 2 bit còn lại (bit 5 và 6)

Vậy làm mình đã thu lại được đoạn bit gốc, tức giá trị của x cần tìm. Với chuỗi bit dài hơn, mình chỉ cần chạy quá trình trên lặp đi lặp lại là được.

Dễ rồi phải không? Mặc dù mình nghĩ ra được ý tưởng mình việc code tốn của mình tận 30 phút... và cuối cùng lại chỉ thành 1 đoạn code ngắn ngủi sau:

def xor(a, b):
    return ''.join(str(int(_a) ^ int(_b)) for _a, _b in zip(a, b))

def shiftsolong(x, bitshift):
    x = '{0:b}'.format(x)
    for i in range(0, len(x) - bitshift):
        x = x[:bitshift*(i+1)] + xor(x[bitshift*i:bitshift*(i+1)], x[bitshift*(i+1):bitshift*(i+2)]) + x[bitshift*(i+2):]
    return int(x, 2)

Ta nói đời về căn bản là buồn mà Thôi tổng hợp lại, thì mình có đoạn code lấy lại giá trị x từ hàm alittlebitharderone(x)

def solvehardone(x):
    x = shiftsolong(x, 2)
    x *= gmpy2.invert(268448390289851351177030176676964262981, 2**128)
    x &= 0xffffffffffffffffffffffffffffffff
    x = shiftsolong(x, 20)
    x *= gmpy2.invert(303397380928069120521467215513016862667, 2**128)
    x &= 0xffffffffffffffffffffffffffffffff
    x = shiftsolong(x, 3)
    x *= gmpy2.invert(281159923981539500379670095774511568603, 2**128)
    x &= 0xffffffffffffffffffffffffffffffff
    x = shiftsolong(x, 19)
    return int(x)

Qua vòng 2 và nhận được flag. Chỉ là không kịp submit nữa...

Nếu có ước muốn trong cuộc đời này, mình sẽ ước có một không gian riêng mà thời gian chảy chậm để ngồi debug trước khi hết giờ FUSEC

2. CRY302 (1000 pts)

1 bài liên quan tới hash, cách thực hiện khá dễ. Full source code bạn có thể xem tại đây

a. Bổ đề

Tóm tắt lại thì mình sẽ được đưa cho 1 số tiền ngẫu nhiên từ 1 tới 2000 và bị bắt phải mua 1 cái FLAG có giá tận 99,999. Kiểu gì cũng không đủ cho được.

Khi mình order 1 vật phẩm bất kỳ, order của mình sẽ có cấu trúc dạng kiểu product=FLAG&price=99999&time=1633845957.70&sign=67df43a8c83ea4ee53ac7bb61cc9a51661f5b55b54153afb942246c11a3ab9a93cb7a1cecb235195eab957fceb3e3daaf3e97f484d29718aea8b0f63e1a3704a (đã được decode từ chuỗi base64 encoded)

Khi nhập lại cái order ở trên để xác nhận mua sản phẩm, order này được kiểm tra các cấu trúc và tính toàn vẹn, cụ thể gồm:

Tồn tại cặp parameter-value sign={sign_value}
Có signature hợp lệsha512(signkey+payment).hexdigest() == signature

Sau khi qua các bài check trên, payment sẽ được truyền vào hàm parse_sql(self, query) để tiến hành extract các parameter tương ứng.

def parse_qsl(self, query):
    m = {}
    parts = query.split(b'&')
    for part in parts:
        key, val = part.split(b'=')
        m[key] = val
    return m

Với cách hàm parse hoạt động như này, giả sử query có 2 cặp giá trị của price (ví dụ như price=99999&price=0) thì giá trị price cuối cùng sẽ được quyết định bởi cái đằng sau. Điều đó đồng nghĩa với việc nếu mình có thể kéo dài cái payment của mình bằng cách append thêm 1 đoạn &price=0, mình có thể mua bất cứ thứ gì trong cửa hàng!

Ý tưởng kéo dài 1 đoạn payment được hash đã đưa mình đến hash length extension attack

b. Hash length extension attack

Hash length extension attack là gì?

Hash length extension attack cho phép mình kéo dài chuỗi văn bản được hash, đồng thời tính toán giá trị hash mới hợp lệ cho chuỗi văn bản được kéo dài ra từ hash của chuỗi văn bản ban đầu.

Nguồn đọc hiểu hash length extension attack

Trước hết, cần phải hiểu được sha512 hoạt động như thế nào đã. Bạn có thể xem tổng quan về hàm sha512 tại đây và xem chi tiết cách sha512 vận hành từng bước 1 tại đây. Thanks for Indian guys

Tiếp đó, mình đọc mô tả cách hash length extension attack hoạt động, và có bản demo tại đây. Thực ra trước có 1 bài blog bằng tiếng Việt cho họ hash SHA luôn, mà giờ trang đấy sập rồi Nên mình sẽ mô tả lại trong bài này để các bạn hiểu dưới góc độ python code, phòng trường hợp các bạn đọc demo trên mạng đều code bằng C và không hiểu gì =)))

Điều kiện để thực hiện hash length extension attack

Để thực hiện được hash length extension attack mà văn bản xác thực có dạng secret_value + public_value, mình cần có đủ 3 dữ kiện:

Độ dài của secret_value, ở trong bài này chính là độ dài của signkey. Bài không cho cụ thể nhưng chỉ cho 24 giá trị khả năng, hoàn toàn có thể bruteforce. Mình không cần giá trị của secret_value!
Giá trị của public_value, ở trong bài này chính là payment
Giá trị hash của secret_value + public_value, ở trong bài này chính là sign

Vậy là bài này hội tụ đủ cả 3 yếu tố để tiến hành rồi.

Tiến hành tấn công thôi!

Mục tiêu của mình bao gồm:

Append thêm 1 đoạn &price=0 vào cuối payment
Tạo ra 1 giá trị sign mới sao cho sha512(signkey+payment) = sign với payment mới

Sơ sơ cơ chế hoạt động của hash length extension attack sẽ như sau.

Cơ chế hoạt động của hàm hash: Hàm hash sha512 sẽ chia input đầu vào thành các khối 1024 bits, mỗi khối lại chia thành từng phần nhỏ h[i]gồm 128 bits. Một tuple (h[0], h[1], h[2], h[3], h[4], h[5], h[6], h[7]) được gọi là current_state của hàm hash hiện tại. current_state sẽ được dùng để tính state cho khối 1024 bits tiếp theo. Hàm xử lý quá trình này gọi là round_function hoặc compress (tùy theo tài liệu). Kết quả cho khối 1024 bits cuối cùng chính là giá trị hash mình thu được.
Cơ chế hoạt động của hash length extension attack: Từ cơ chế hoạt động trên của hàm hash, mình có thể thấy rằng chỉ cần biết được current_state và khối 1024 bits cuối cùng, mình hoàn toàn có thể tính toán state cho khối 1024 bits tiếp theo, trong đó, khối 1024 bits sẽ có giá trị tùy ý mình thích. Đó cũng chính là giá trị hash mới với chuỗi văn bản được kéo dài.

Khá là đơn giản phải không. Giờ mình sẽ đi vào cụ thể nhé:

Order FLAG, nhận giá trị order trả về product=FLAG&price=99999&time=1633849486.36&sign=275e626950c677c05a669e4e9d73f015858ca2b477335b2e99f419f9f0bc860736e95bd87de1226764c70f8c59029edc10e6b2a514342bb85f0c29fe24b9d3e2. Tách payment và sign riêng.
Padding cho payment để payment có dạng $k*1024$ , và lấy block cuối cùng, thu được product=FLAG&price=99999&time=1633849486.36\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x02P. Vốn chuỗi ban đầu không dài hơn 1024 bits nên cũng chỉ có block duy nhất. Trong phần ví dụ này, mình giả sử độ dài của signkey bằng 31. Cơ chế padding mình đính kèm nguồn ở trên.
Append chuỗi &price=0 vào chuỗi đã được padding ở trên. Lại tạo 1 khối 1024 bits có chứa &price=0 bằng cách padding, thu được &price=0\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x018
Extract state từ giá trị sign, sau đó đưa state cùng khối 1024 bits có chứa &price=0 ở trên vào hàm compress của sha512, thu được giá trị sign mới bằng ad38b9ceecbdf41de6bb33970a473ecc1c500935e2cfd90007be639fa6754b6272c45340fca0f173090748722cc1e25e3440cc9975c3b712a8cabe7809cf6d7f
Nối chuỗi payment mới và sign mới vào với nhau, chuyển lên server và lấy flag. order mới sẽ là product=FLAG&price=99999&time=1633849486.36\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x02P&price=0

Vậy là xong!

c. Full code exploit

Vì bài không cho giá trị cụ thể của độ dài signkey, nên mình phải viết 1 đoạn code chạy tự động trong khoảng giá trị $[8, 32]$ . Full code exploit có thể xem ở đây. Trong code này, mình có sử dụng lại thư viện hlextend của stephenbradshaw trên github, với một chút chỉnh sửa để output ra có dạng byte thay vì string.

def solve():
    [REDACTED]

    #order
    output = recvuntil(clientSock, b'Your choice:')
    clientSock.sendall(b'2\n')
    output = recvuntil(clientSock, b'ID:')
    clientSock.sendall(b'6\n')
    output = recvuntil(clientSock, b'Your choice:')
    order = output.split(b'\n')[0][len('Your order:'):].strip()
    order = b64decode(order).decode('latin-1')

    sp = order.rfind('&sign=')
    sign = order[sp+6:]
    payment = order[:sp]
    append_msg = '&price=0'
    

    for i in range(8, 33):
        sha = hlextend.new('sha512')
        new_payment = sha.extend(append_msg, payment, i, sign)
        new_sign = sha.hexdigest()
        new_order = new_payment + b'&sign=' + new_sign.encode()
        new_order = b64encode(new_order)

        #confirm order
        clientSock.sendall(b'3\n')
        output = recvuntil(clientSock, b'Your order:')
        clientSock.sendall(new_order + b'\n')
        output = recvuntil(clientSock, b'Your choice:')
        if b'FUSec{' in output:
            flag = output.decode()[output.index(b'FUSec{'):output.index(b'}')+1]
            print(flag)
            break

Flag FUSec{th1s_1s_4n_0ld_vul_bUt...}

3. CRY303 (991 pts)

Một bài siêu khó về Knapsack cipher sử dụng LLL (Lenstra–Lenstra–Lovász), hay còn gọi là Latice Reducation Technique, để giải.

Nói thật thì bài này mình cũng không tự làm được lúc tham gia giải CTF, nhưng search google được 1 bài giống tới 90%, nên chỉ đọc hiểu code rồi giải lại. Bởi vì bài cũng không có gì khác biệt mấy, nên mình để nguồn bài gốc ở đây để các bạn đọc vậy.

Link github exploit code + writeup: https://github.com/pcw109550/write-up/tree/master/2020/KAPO/Baby_Bubmi
Bài viết cụ thể giải thích cơ chế hoạt động: http://www.secmem.org/blog/2020/09/20/poka-science-war-hacking/

Đề bài này và code giải (đã sửa theo bài) mình để ở github của mình.

Thế là hết crypto rồi. Nếu mà kịp giải hết thì mình cũng mạnh dạn insert bomman meme gáy... nhưng không được nên gà không gáy nữa...