Ứng dụng của ECC: Trao đổi khóa Diffie-Hellman
Bài đăng này đã không được cập nhật trong 5 năm

Trong bài viết trước, mình đã Giới thiệu về Hệ mật trên đường cong Elliptic và nói rằng ECC được ứng dụng nhiều trong mật mã, nhưng ứng dụng ở đâu? để làm gì? thì chưa đề cập đến. Trong bài viết này, mình sẽ chia sẻ về ứng dụng của ECC trong việc trao đổi khóa bí mật, dựa trên giao thức trao đổi khóa Diffie-Hellman.
1. Trao đổi khóa Diffie-Hellman
1.1. Vấn đề của các Hệ mật khóa đối xứng
Trước khi nói về trao đổi khóa Diffie-Hellman, mình muốn nói lại các kiến thức cơ bản một chút để các bạn mới tiếp xúc vẫn có thể hiểu được vấn đề.
Các hệ mật được chia thành 2 loại:
- Hệ mật khóa đối xứng
- Hệ mật khóa bất đối xứng (hệ mật khóa công khai)
Cả 2 loại đều có những ưu - nhược điểm riêng, và các hệ mật thuộc 1 trong 2 nhóm trên đều có chỗ đứng riêng của chúng. Với hệ mật khóa đối xứng, do sử dụng cùng 1 khóa cho cả 2 quá trình giải mã / mã hóa, nên các hệ mật thuộc nhóm này có tốc độ mã hóa / giải mã nhanh, dễ cài đặt. Tuy nhiên việc này cũng tạo ra 1 vấn đề, đó là làm sao để giữ bí mật khóa chung.

Để 2 người có thể cùng sở hữu khóa chung, họ bắt buộc phải trao đổi và thỏa thuận với nhau. Ngày nay, công đoạn này chủ yếu diễn ra trên môi trường mạng Internet công cộng - nơi không được an toàn cho lắm. Trong quá trình thỏa thuận và trao đổi khóa, có khả năng khóa chung (khóa bí mật) sẽ bị các kẻ xấu lấy được. Nhờ thế các thông điệp do 2 bên trao đổi với nhau, cũng sẽ bị kẻ này dễ dàng giải mã và đọc được.
1.2. Trao đổi khóa chung
Giao thức trao đổi khóa Diffie-Hellman được sử dụng để khắc phục nhược điểm trên của các hệ mật khóa đối xứng. Bằng cách cung cấp một quy trình kết hợp với việc sử dụng các bài toán khó, giao thức cho phép 2 bên thỏa thuận và xác định khóa chung mà không cần truyền khóa qua môi trường mạng Internet.
Cụ thể giao thức Diffie-Hellman hoạt động thế nào thì chúng ta sẽ cùng xem ví dụ sau, vẫn là câu chuyện về Bob và Alice, nhưng lần này họ sẽ chơi trò "pha màu".
Đầu tiên, bản thân Bob và Alice đều tự chọn cho mình 1 màu bí mật, không ai ngoài chính bản thân họ biết về màu đó. Ngoài môi trường mạng Internet công khai thì có sẵn 1 màu, công khai, và ai cũng biết màu đó là gì. Ở đây, Alice chọn cho mình màu đỏ, Bob chọn màu xanh lá, còn màu công khai ngoài Internet là màu vàng.
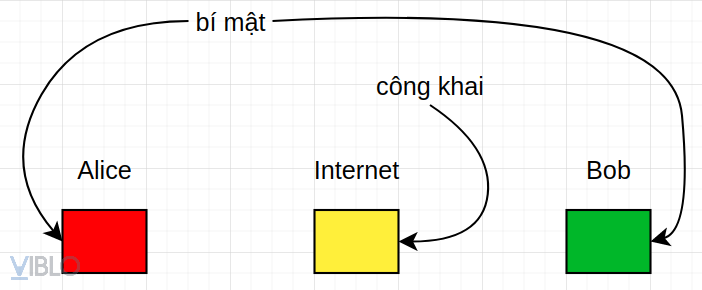
Bước 2: Alice và Bob sẽ trộn màu bí mật của họ với màu công khai
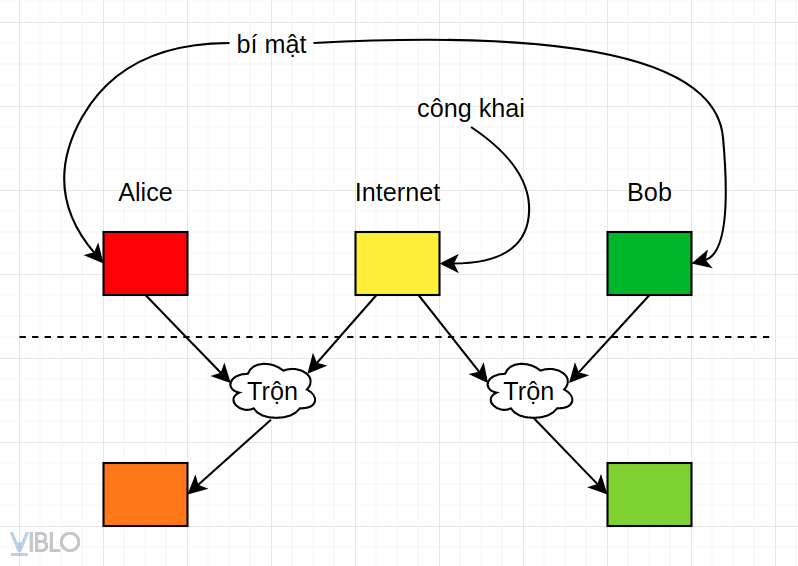
Bước 3: Giờ thì Bob và Alice đã sẵn sàng cho việc thỏa thuận khóa. Họ sẽ gửi màu vừa trộn được ở Bước 2 cho nhau qua môi trường Internet. Tất nhiên giờ kẻ xấu cũng có thể nhận được 2 màu mới này, nhưng chẳng sao cả.
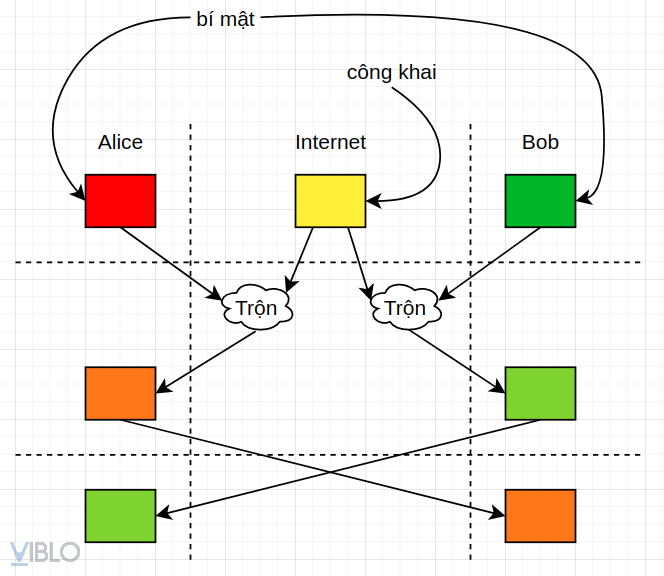
Bước 4: Mỗi người sẽ trộn màu bí mật từ đầu của mình, với màu vừa nhận được. Và màu trộn ra cuối cùng này chính là màu chung của cả 2.
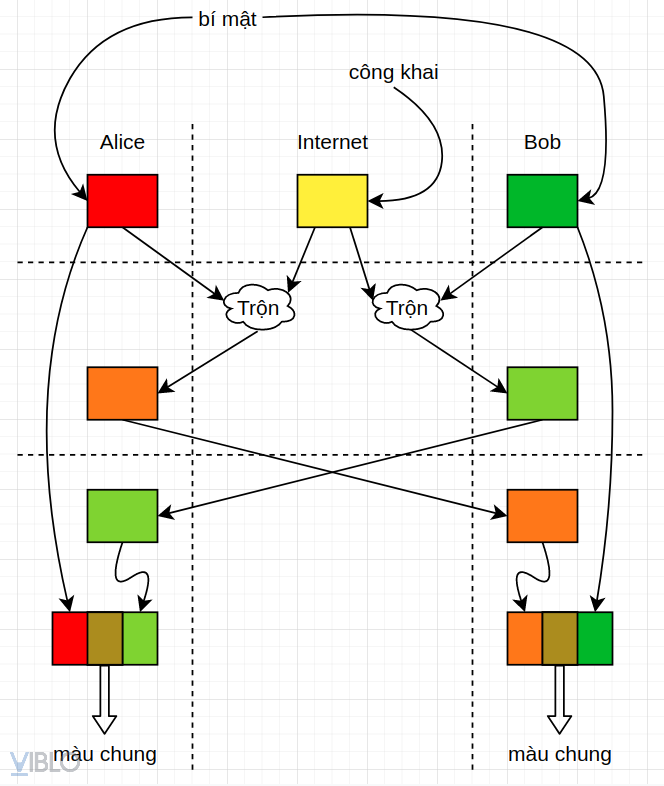
Bản chất màu chung bí mật này được tạo thành từ 3 màu:
- Màu bí mật của Alice (A)
- Màu bí mật của Bob (B)
- Màu công khai trên Internet (P)
Trong toàn bộ quá trình thực hiện thỏa thuận khóa chung, kẻ xấu chỉ có những dữ liệu: P, (A , P), (B , P). Từ đó thì không thể trộn ra được màu chung giữa Alice và Bob.
Nguyên lý hoạt động của giao thức trao đổi khóa Diffie-Hellman cơ bản là như vậy. Khi áp dụng thực tế, người ta sẽ sử dụng các phép tính và tính chất toán học để cho ra hiệu quả tương tự việc "trộn màu"
2. Trao đổi khóa Diffie-Hellman trong ECC
Bây giờ chúng ta sẽ làm thật luôn, sử dụng code python để demo quá trình trao đổi và thỏa thuận khóa:
- Đường cong sử dụng: secp256k1
- Khóa công khai: điểm cơ sở G của đường cong
- Khóa bí mật của Alice: số nguyên A
- Khóa bí mật của Bob: số nguyên B
Mình sẽ sử dụng thư viện ECPy để tính toán. Code:
from ecpy.curves import Curve
cv = Curve.get_curve('secp256k1')
G = cv.generator
print("Generator point (Public key): \n\tG =", G) # Public color
A = 2 # Alice's private color
B = 3 # Bob's private color
print("\nAlice's private key: \n\tA =", A)
print("Bob's private key: \n\tB =", B)
AG = A*G # Alice's private color mix with Public color
BG = B*G # Bob's private color mix with Public color
print("\nAlice's mixed key: \n\tAG =", AG)
print("Bob's mixed key: \n\tBG =", BG)
B_AG = B*AG
A_BG = A*BG
print("\nPrivate key of Alice and Bob (Calculated by Alice): \n\tA*(BG) =", A_BG)
print("Private key of Alice and Bob (Calculated by Bob): \n\tB*(AG) =", B_AG)
# Check
print("\nIs AG on the curve?", cv.is_on_curve(AG))
print("Is BG on the curve?", cv.is_on_curve(BG))
print("Is ABG on the curve?", cv.is_on_curve(A_BG))
Kết quả:
Generator point (Public key):
G = (0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798 , 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)
Alice's private key:
A = 2
Bob's private key:
B = 3
Alice's mixed key:
AG = (0xc6047f9441ed7d6d3045406e95c07cd85c778e4b8cef3ca7abac09b95c709ee5 , 0x1ae168fea63dc339a3c58419466ceaeef7f632653266d0e1236431a950cfe52a)
Bob's mixed key:
BG = (0xf9308a019258c31049344f85f89d5229b531c845836f99b08601f113bce036f9 , 0x388f7b0f632de8140fe337e62a37f3566500a99934c2231b6cb9fd7584b8e672)
Private key of Alice and Bob (Calculated by Alice):
A*(BG) = (0xfff97bd5755eeea420453a14355235d382f6472f8568a18b2f057a1460297556 , 0xae12777aacfbb620f3be96017f45c560de80f0f6518fe4a03c870c36b075f297)
Private key of Alice and Bob (Calculated by Bob):
B*(AG) = (0xfff97bd5755eeea420453a14355235d382f6472f8568a18b2f057a1460297556 , 0xae12777aacfbb620f3be96017f45c560de80f0f6518fe4a03c870c36b075f297)
Is AG on the curve? True
Is BG on the curve? True
Is ABG on the curve? True
Sau khi đã có được điểm ABG trên đường cong E rồi, chúng ta có thể sử dụng tọa độ của điểm này để thực hiện các thuật toán mã hóa dựa trên đường cong Elliptic. Hoặc nếu không muốn, chúng ta vẫn có thể sử dụng tọa độ X hoặc Y để làm khóa chung cho các thuật toán mã hóa khóa đối xứng.
Do tính chất của đường cong Elliptic, các phép tính cộng và nhân trên đường cong là trap door - tính xuôi thì dễ, nhưng rất khó để tính ngược lại. Để tìm được khóa chung giữa Alice và Bob, kẻ xấu bắt buộc phải tìm được khóa bí mật của 2 người bằng cách giải 2 bài toán Logarit rời rạc - vốn rất khó để giải ra trong thời gian đa thức.
References:
- Giáo trình Mật mã học nâng cao, Học viện Công nghệ Bưu chính Viễn Thông.
- Hệ mật mã hóa công khai dựa trên đường cong Elliptic của thầy Đặng Minh Tuấn.
- http://antoanthongtin.vn/gp-mat-ma/mat-ma-duong-cong-elliptic-va-mat-ma-hang-nhe-101337
- https://viblo.asia/p/ecdsa-he-mat-dua-tren-duong-cong-elliptic-va-ung-dung-trong-blockchain-XL6lA4oDZek
- https://medium.com/coinmonks/elliptic-curve-cryptography-6de8fc748b8b
- https://www.youtube.com/watch?v=m-ccKQHtGQ8
- https://www.youtube.com/watch?v=NF1pwjL9-DE
- https://www.youtube.com/watch?v=nybVFJVXbww
- https://www.youtube.com/watch?v=dCvB-mhkT0w
- https://voer.edu.vn/m/phan-phoi-khoa-va-thoa-thuan-khoa/2985171b
- https://www.youtube.com/watch?v=GSIDS_lvRv4
- https://www.youtube.com/watch?v=NmM9HA2MQGI
- https://www.youtube.com/watch?v=yDXiDOJgxmg
- https://www.youtube.com/watch?v=Yjrfm_oRO0w
All rights reserved
