Từ lý thuyết lượng tử đến Quantum Neural Network (phần 1) - Giới thiệu cơ bản về tính toán lượng tử
Bài đăng này đã không được cập nhật trong 3 năm
Lời mở đầu
Với máy tính bình thường, đơn vị thông tin nhỏ nhất là bit và có 2 giá trị 0 hoặc 1. Tất cả những ứng dụng, ảnh, văn bản,... mà chúng ta được nhìn thấy hay sử dụng qua máy tính đều được cấu thành từ bit. Thế nhưng bit có thực sự phản ánh được toàn bộ thông tin trong vũ trụ mà chúng ta đang sống ? Điều này không thực sự đúng, thế giới của chúng ta không đơn giản chỉ gói gọn trong 2 con số 0 và 1. Thay vào đó các nhà khoa học đã mở ra 1 lĩnh vực mới, người ta xem xét các khía cạnh của tự nhiên dưới góc độ vi mô (phân tử, nguyên tử, hạ nguyên tử). Đây chính là mở đầu cho cơ học lượng tử, hình thành cơ sở cho các lý thuyết lượng tử trong đó có tính toán lượng tử ( Quantum Computing)
Tính toán lượng tử là một loại tính toán khai thác các thuộc tính chung của các quy luật trong cơ học lượng tử, chẳng hạn như chồng chất, giao thoa và rối loạn, để thực hiện các phép tính. Các thiết bị thực hiện tính toán lượng tử được gọi là máy tính lượng tử. Trong phần này, mình sẽ giới thiệu sơ qua về lý thuyết cơ bản của tính toán lượng tử đến các bạn.
-
Note: không gian trạng thái và ký hiệu bra / ket
- Ket: = => = , =
- Bra: = => = , =
- = =
1. Photon polarization
Từ thí nghiệm phân cực photon đến cơ học lượng tử
Trạng thái phân cực của 1 photon có thể được mô hình hóa bởi 1 vector theo 1 hướng nhất định, bất kỳ 1 sự phân cực nào đều có thể được biểu diễn dưới dạng kết hợp tuyến tính của 2 vector cơ sở ( phân cực đứng ) và ( phân cực ngang) với a,b là số phức sao cho .
Xác suất để 1 trạng thái được xem như 1 vector cơ sở là bình phương chuẩn của thành phần biên độ.
Ví dụ với trạng thái được đo lường như với xác suất và như với xác suất
Cơ học lượng tử có thể giải thích thí nghiệm phân cực như sau. Một thấu kính polaroid đo trạng thái lượng tử của các photon đối với cơ sở bao gồm vector phân cực với nó cùng 1 vector trực giao với sự phân cực đó. Các photon sau khi được tính toán cho phù hợp với phân cực của bộ lọc thì sẽ được đi qua. Những phần khác sẽ được phản xạ lại theo phân cực vuông góc với phân cực của bộ lọc. Ví dụ, cho filter A đo lường phân cực của photon với vector cơ sở tương ứng với sự phân cực của nó. Những photon đi qua bộ lọc A đều có sự phân cực ngang . Những photon còn lại được phản xạ bởi bộ lọc đều có phân cực thẳng đứng
Giả sử 1 nguồn sáng tạo photon với các phân cực ngẫu nhiên, bộ lọc A tính toán ra 50% số photon là phân cực ngang, có trạng thái . Bộ lọc C sẽ xem xét những photon đó theo phân cực , nhưng trạng thái sẽ được ánh xạ lên với xác suất 0 => không photon nào đi qua bộ lọc C. Vì thế phải có bộ lọc B tính toán trạng thái lượng tử với cơ sở :
Hoặc có thể viết là . Trong đó và
=> Photon đi qua A có trạng thái với xác suất 50%, sau đó qua B với trạng thái với xác suất 50%, cuối cùng qua C với trạng thái với xác suất 50%. Vì vậy số lượng photon sẽ đi qua A B C
2. Quantum bit
Quantum bit (qubit) là một khái niệm cơ bản và quan trọng nhất trong lĩnh vực khoa học thông tin lượng tử. Qubit được định nghĩa là một đối tượng dùng để truyền tải thông tin trên nền tảng lý thuyết thông tin lượng tử và tính toán trên máy tính lượng tử. Thuật ngữ này được đề xuất bởi Benjamin Schumacher trong bài báo của ông về mã hóa lượng tử vào năm 1993.
Qubit được xây dựng như là một đối tượng toán học với những tính chất đặc biệt. Tuy nhiên, điều đó không có nghĩa qubit không có tính chất vật lý. Ngược lại, tùy vào hệ đang xét mà qubit sẽ được biểu diễn dưới nhiều dạng khác nhau. Trong nghiên cứu lý thuyết, qubit thường được mô tả như một hạt có spin ½. Khái niệm qubit đóng vai trò quan trọng trong nghiên cứu Vật lý lượng tử hiện đại: là viên gạch đầu tiên trong xây dựng lý thuyết kết dính lượng tử, tính toán lượng tử, viễn tải lượng tử và truyền thông lượng tử.
- Trong tính toán lượng tử, 2 trạng thái được dùng để biểu diễn 2 bit 0, 1. Nhưng khác ở chỗ qubit có thể dùng dưới dạng kết hợp tuyến tính của như , trong đó a,b là số phức sao cho .
2.1 Biểu diễn toán học của qubit
Qubit là một hệ lượng tử có hai mức được biểu diễn trong không gian Hilbert hai chiều. Trong không gian này, một cặp trạng thái lượng tử trực giao và chuẩn hóa được chọn để mô tả một hệ vật lý:
Dễ dàng thấy rằng các trạng thái của qubit tương ứng với các giá trị nhị phân 0 và 1 của bit cổ điển. Các trạng thái này lập thành một cơ sở tính toán. Điểm khác biệt quan trọng chính là bit cổ điển chỉ có thể biểu diễn tại một thời điểm duy nhất một trạng thái 0 hoặc 1. Trong khi đó, với Chồng chập lượng tử|nguyên lý chồng chập, qubit có thể tạo thành một tổ hợp tuyến tính các trạng thái. Một trạng thái bất kỳ của qubit được viết dưới dạng:
trong đó,a và b là các số phức và thỏa mãn điều kiện chuẩn hóa:
Hai biểu thức trên cho biết khi sau khi tiến hành phép đo, kết quả thu được hoặc 0 với xác suất hoặc 1 với xác suất . Biểu thức tổng quát cho qubit trình bày ở trên có một ý nghĩa quan trọng: nó cho biết qubit là một sự Chồng chập lượng tử|chồng chập trạng thái kết hợp giữa và thay vì một hỗn hợp không kết hợp.
2.2 Biểu diễn qubit bằng quả cầu Bloch
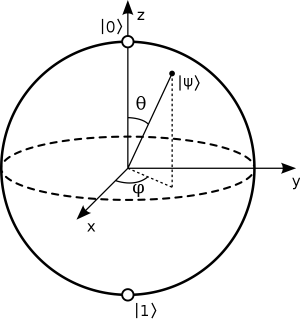
Quả cầu Bloch là một quả cầu có bán kính đơn vị. Nó được sử dụng để biểu diễn các qubit một cách trực quan. Vị trí của mỗi qubit được xác định rõ ràng thông qua các tham số và
Điều kiện chuẩn hóa cho phép qubit được biểu diễn ở dạng tổng quát và tường minh hơn:
với các tham số và là các số thực. Giá trị pha toàn cục không quan sát được nên có thể bỏ. Khi đó, biểu thức cho qubit có dạng:
Các tham số và xác định một điểm trên một quả cầu đơn vị 3 chiều, được gọi là quả cầu Bloch. Đầu tiên là quả cầu Bloch chỉ là biểu diễn toán học và không có cách nào xác định hướng của qubit trong quả cầu này. Thứ hai, kết quả của phép đo trên qubit luôn cho 0 hoặc 1 với một xác suất cho trước. Sau phép đo, hàm sóng bị suy sụp.
Một điểm cần lưu ý là khi biểu diễn bằng quả cầu Bloch, những qubit nào trực giao với nhau thì vector bán kính của chúng đối song song với nhau. Đơn cử, các qubit và lần lượt được xác định tại điểm cực bắc và nam của quả cầu và chúng trực giao với nhau.
-
Multiple qubit
Giả sử V và W là 2 không gian phức 2 chiều với vơ sở {v1, v2} và {w1, w2}, phép nhân tensor của V và W có cơ sở {v1 w1, v2 w2, v1 w2, v2 w1} => không gian trạng thái của 2 qubit với mỗi cơ sở {} sẽ có cở sở {}, tương đương với {. Với 3-qubit cũng sẽ tương tự như vậy: {. Hệ thống n qubit có vector cơ sở.
3. Lợi thế của thuật toán lượng tử
Ở phần này mình sẽ nói qua về các quy luật tuy cơ bản nhưng cũng rất quan trọng trong cơ học lượng tử đó là giao thoa, chồng chập, rối loạn.
Nguyên lý chồng chập có thể được phát biểu một cách ngắn gọn như sau : nếu 1 hệ lượng tử có thể được đo đạc ở 1 trong 2 trạng thái A hoặc B với các tính chất khác nhau thì nó cũng có thể được đo đạc ở trạng thái tổ hợp của chúng: , với là các số bất kỳ. Mỗi tổ hợp này là 1 chồng chập và có các tính chất vật lý khác nhau. Nhờ có tính chất chồng chập mà qubit có thể có Nguyên lý chồng chập trong thuyết lượng tử được gọi là chồng chập lượng tử
Rối lượng tử là một hiệu ứng trong cơ học lượng tử trong đó trạng thái lượng tử của hai hay nhiều vật thể có liên hệ với nhau, dù chúng cách xa tới mức nào, thậm chí là tới khoảng cách lên tới cả nhiều năm ánh sáng, phép đo thực hiện trên vật thể này sẽ ảnh hưởng trực tiếp đến trạng thái lượng tử trên vật thể vướng víu lượng tử với nó. Ví dụ: Có 2 photon sao cho spin của cặp photon này là 0 (zero), khi photon thứ nhất quay theo chiều kim đồng hồ thì bằng 1 cách nào đó photon thứ 2 sẽ quay ngược chiều kim đồng hồ sao cho tổng spin của chúng bằng 0 (zero) bất chấp khoảng cách của chúng là bao xa hoặc trong bất kỳ trường hợp nào mà không cần bất kể lực tác động nào khác. Điều nay vi phạm tất cả các quy tắc vật lý thông thường. Nó được xem như phương thức liên lạc của tương lai khi tốc độ của nó gần như ngay lập tức bất chấp đang ở không-thời-gian nào (kể cả trong hoặc phía bên kia Hố Đen), thay thế phương thức truyền tín hiệu trong vũ trụ hiện nay của con người là dùng sóng vô tuyến có tốc độ bằng với tốc độ ánh sáng, và không thể sử dụng trong nhiều trường hợp đặc biệt.
Rối lượng tử thường được mô tả với hai photon có sự liên hệ với nhau, trạng thái của photon này quyết định trạng thái của photon kia. Nếu đo được trạng thái của một photon thì ngay lập tức sẽ biết được trạng thái của photon có liên hệ với nó. Điều này cũng có nghĩa là nếu ta buộc photon này có một trạng thái nào đó thì lập tức photon kia cũng có trạng thái tương ứng.
Giao thoa lượng tử có sự tương đồng khá lớn với giao thoa sóng ánh sáng, nó là sự kết hợp của các hạt cấu trúc trong quá trình giao thoa tạo nên các bước sóng đặc biệt. Gọi là hàm sóng trong phương trình Schrödinger cho 1 vật thể trong trạng thái lượng tử. Ta có xác suất ta có thể quan sát vật thể tại điểm là , trong đó là số phức liên hợp của . Giao thoa lượng tử sẽ được biểu diễn theo hàm xác suất trên khi hàm sóng được biểu diễn dưới dạng chồng chập tuyến tính 2 đại lượng:
Trong đó được gọi là số hạng giao thoa. Nếu số hạng này không có trong tất cả , thì sẽ không có giao thoa lượng tử liên quan đến A và B.
Linh hồn của thuật toán lượng tử nằm ở phương pháp sử dụng rối lượng tử và song song lượng tử để các kết quả mong muốn được đo với xác suất cao. Một số kỹ thuật thường được biết đến:
- Khuếch đại các giá trị đầu ra mong muốn: ý tưởng chung là biến đổi trạng thái sao cho các giá trị mong muốn có biên độ lớn hơn từ đó có xác suất được đo cao hơn
- Tìm tính chất chung của tất cả các giá trị trong thuật toán lượng tử. Ý tưởng này được khai thác trong thuật toán Shor, sử dụng phép biến đổi Fourier lượng tử để thu được chu kỳ của f.
Lời kết
Như vậy, trong bài viết này mình đã giới thiệu sơ qua một số kiến thức cơ bản trong tính toán lượng tử. Cảm ơn các bạn đã theo dõi bài viết của mình. Hy vọng bài viết mang lại nhiều góc nhìn cho các bạn về Quantum Computing. Các bạn hãy theo dõi các bài viết tiếp theo trong chuỗi bài viết về chủ đề này của mình nhé.
Tài liệu tham khảo
All rights reserved