Thuật toán tối ưu adam

Vấn đề tối ưu trong neural network 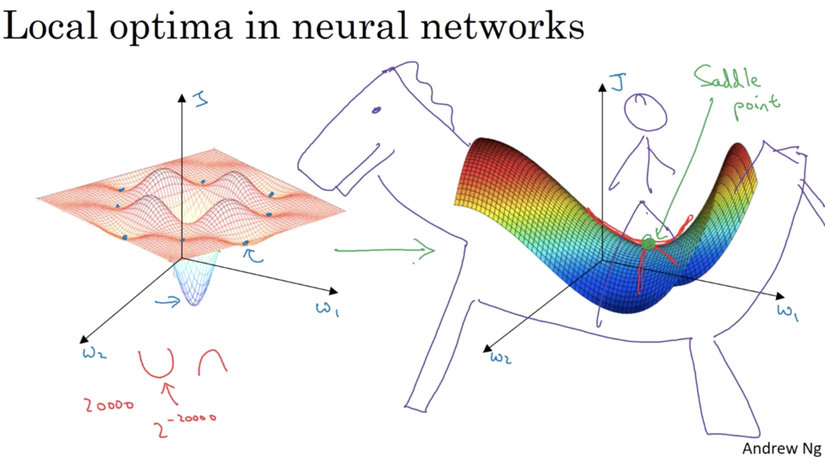Các lợi ích của thuật toán Adam

1. Không khó khăn để implement
2. Độ phức tạp hiệu quả
3. Ít bộ nhớ yêu cầu.
4. Thích hợp với các bài toán có độ biến thiên không ổn định và dữ liệu traning phân mảnh.
5. Các siêu tham số được biến thiên một cách hiệu quả và yêu cầu ít điều chỉnh

Để tìm hiểu Adam làm việc như thế nào, chúng ta cùng lượt sơ các thuật toán tối ưu

1. SGD

Giả sử ta có vector tham số x và đạo hàm dx, thì form update cơ bản là:

x += - learning_rate * dx

2. SGD with Momentum (Momentum optimization)

• Dưới góc nhìn vật lí, SGD với momentum giúp cho việc hội tụ có gia tốc, làm nhanh quá trình hội tụ trên các đường cong có độ dốc lớn, nhưng cũng đồng thời làm giảm sự dao dộng khi gần hội tụ.
• Công thức tương tự trên nhưng chúng ta thêm tích vận tốc của lần trước vào và hệ số gramma thường bằng 0.9

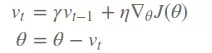
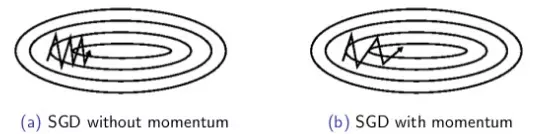
3. Nesterov accelerated gradient

• Cách thức này có 1 ít khác biệt so với momentum update, với momentum update ta tính toán đạo hàm tại vị trí hiện hành rồi sau đó làm 1 cú nhảy tới dựa trên vector momentum trước đó, với Nesterov momentum thay vì tính toán đạo hàm tại điểm hiện hành, chúng ta dựa vào vector momentum cũ để tính toán vị trí sắp tới, rồi sau đó mới dùng đạo hàm tại vị trí mới để correct lại:
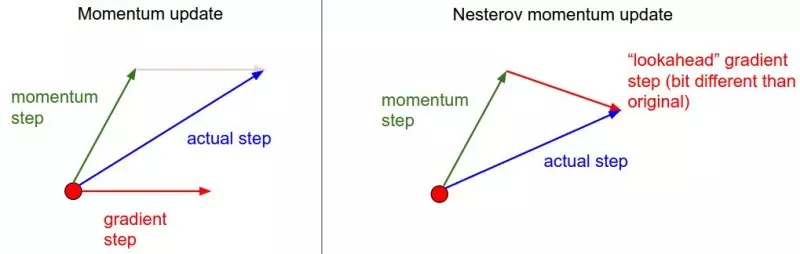
• Theo sau là công thức:

x_ahead = x + mu * v
# evaluate dx_ahead (the gradient at x_ahead instead of at x)
v = mu * v - learning_rate * dx_ahead
x += v

4. Adagrad

• Không giống như các cách thức trước, learning rate hầu như giống nhau cho quá trình learning, adagrad coi learning rate cũng là một tham số

• Nó update tạo các update lớn với các dữ liệu khác biệt nhiều và các update nhỏ cho các dữ liệu ít khác biệt

• Adagrad chia learning rate với tổng bình phương của lịch sử biến thiên (đạo hàm)

  

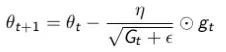
• Trong đó ϵ là hệ số để tránh lỗi chia cho 0, default là 1e−8

• G là một diagonal matrix nơi mà mỗi phần tử (i,i) là bình phương của đạo hàm vector tham số tại thời điểm t

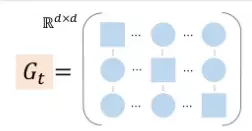
• Một lợi ích dễ thấy của Adagrad là tránh việc điều chỉnh learning rate bằng tay, thường sẽ để default là 0.01 và thuật toán sau đó sẽ tự động điều chỉnh.

• Một điểm yếu của Adagrad là tổng bình phương biến thiên sẽ lớn dần theo thời gian cho đến khi nó làm learning rate cực kì nhỏ, làm việc traning trở nên đóng băng.

5. Adadelta

• Adadelta sinh ra để làm giảm nhược điểm của Adagrad (việc làm thay đổi learning rate theo tính đơn điệu giảm)

• Nó giới hạn sự tích lũy của độ biến thiên tới một giới hạn nhất định

• Để làm được điều trên nó đưa ra khái niệm, running average phụ thuộc vào trung bình trước và độ dốc hiện tại.

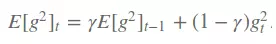
• Gramma ở đây tương tự như với momentum xấp xỉ 0.9.
• Nó còn đưa ra moment thứ 2 là bình phương của tham số update

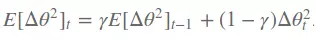
• Tóm tắt công thức:

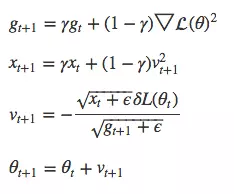
• Chuyển động của AdamDelta:

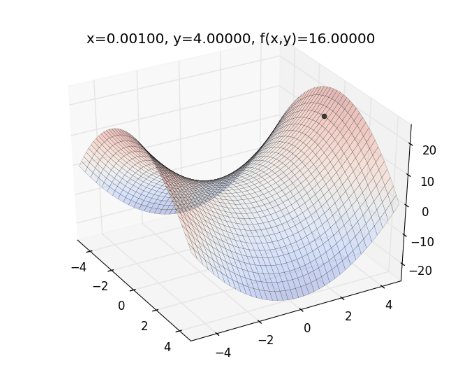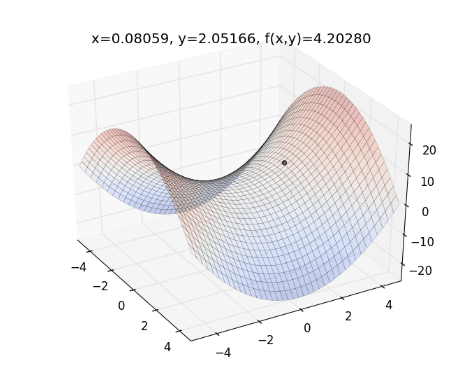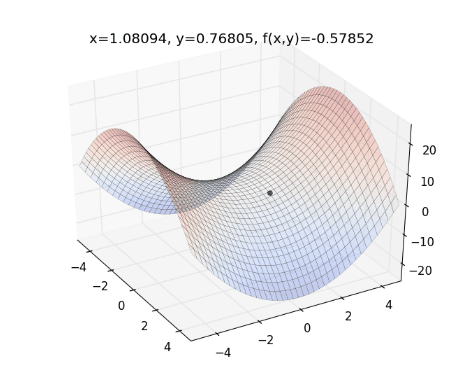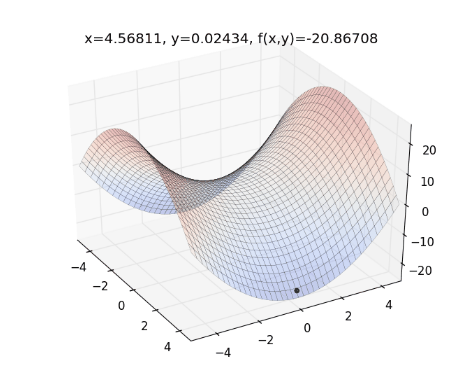
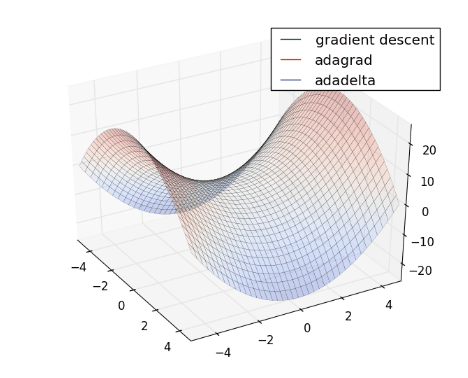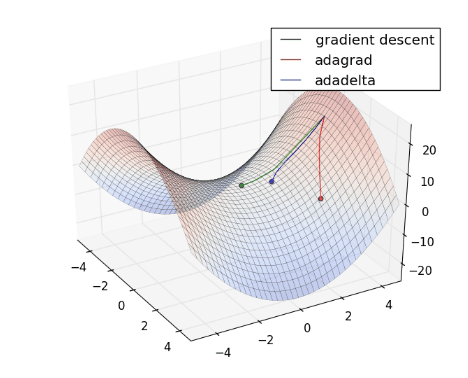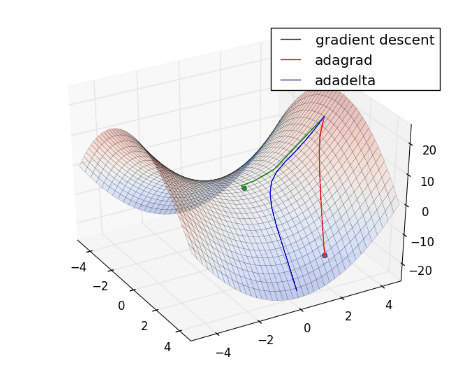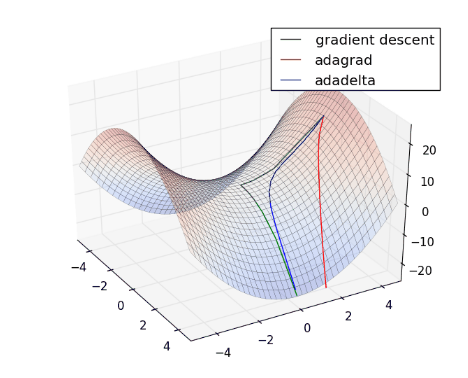
6. RMSprop

cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

• Nó sinh ra cũng để giải quyết vấn đề của Adagrad
• Nó giống với vector update đầu tiên của adadelta

8. Adam

• Giống với Adadelta và RMSprop, nó duy trì trung bình bình phương độ dốc (slope) quá khứ vt và cũng đồng thời duy trì trung bình độ dốc quá khứ mt, giống momentum.
• Trong khi momentum giống như một quả cầu lao xuống dốc, thì Adam lại giống như một quả cầu rất nặng và có ma sát (friction), nhờ vậy nó dễ dàng vượt qua local minimum và đạt tới điểm tối ưu nhất (flat minimum)
• Nó đạt được hiệu ứng Heavy Ball with Friction (HBF) nhờ vào hệ số (mt/ sqrt(vt))

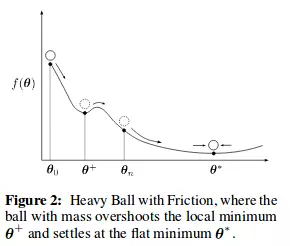
• Công thức update của nó là:

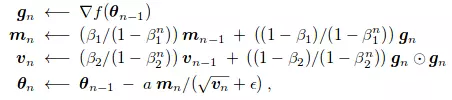
Tổng kết các công thức tối ưu

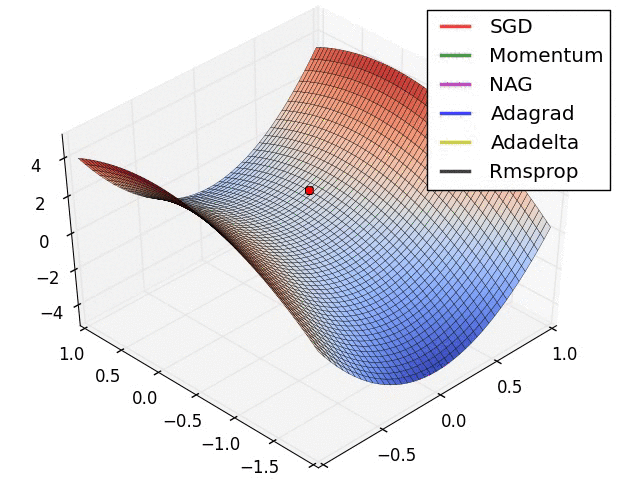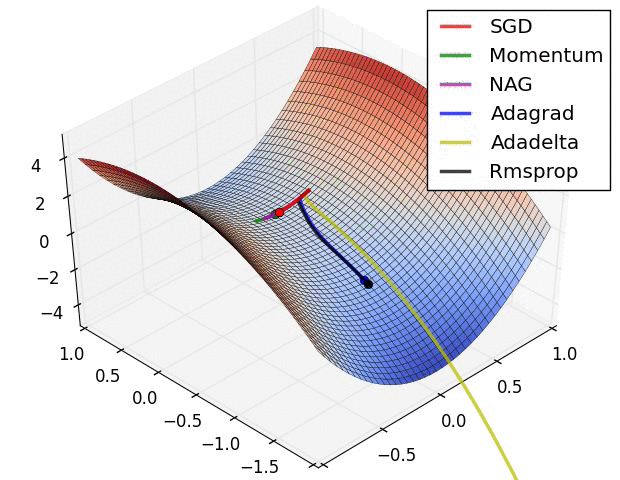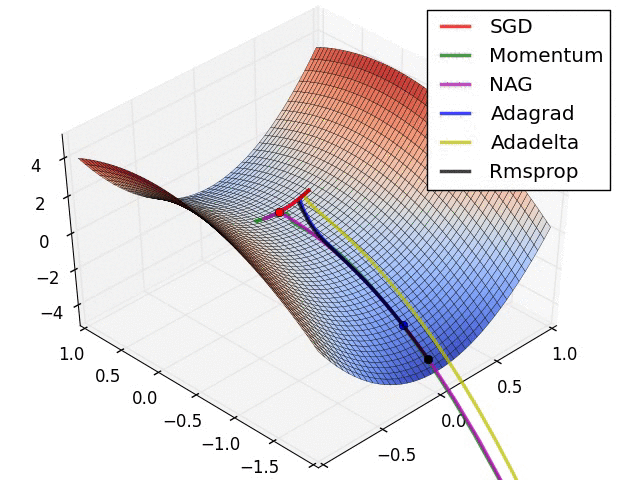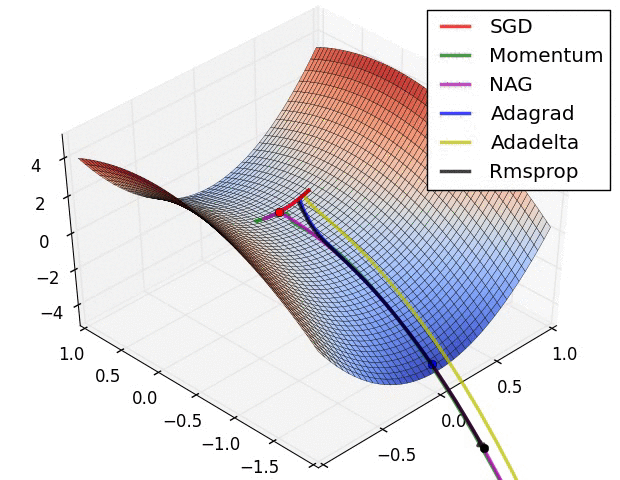
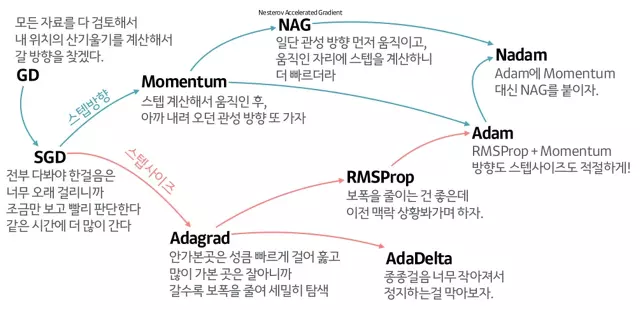
Reference:

• GANs Trained by a Two Time-Scale Update Rule, Converge to a Local Nash Equilibrium (https://arxiv.org/pdf/1706.08500.pdf)
• An overview of gradient descent optimization algorithms (http://ruder.io/optimizing-gradient-descent/index.html)
• Gentle Introduction to the Adam Optimization Algorithm for Deep Learning (https://machinelearningmastery.com/adam-optimization-algorithm-for-deep-learning/)