Thuật toán Naive Bayes

1.1 Lý thuyết

Các lý thuyết về xác suất

Gọi A, B và C là các sự kiện trong một phép thử:

• Các công thức xác suất:

o Xác suất có điều kiện: Xác suất xảy ra sự kiện A với điều kiện sự kiện B đã xảy ra gọi là xác suất có điều kiện B của sự kiện A:

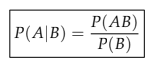
o Công thức nhân xác suất:

o Công thức cộng xác suất:

o Công thức xác suất đầy đủ

Định lý Bayes và các khái niệm liên quan

$$\operatorname { Xét } A _ { 1 } , A _ { 2 } , \ldots A _ { n }$$

là hệ đầy đủ và B là biến cố liên quan. Ta có công thức Bayes

$$\stackrel { \ } { P } ( A _ { i } | B ) = \frac { P ( A _ { i } ) * P ( B | A _ { i } ) } { P ( B ) } \quad \forall i = 1 , 2 , 3 , . .$$

Trong đó: Các xác suất P(Ai), i = 1, 2, . . . , n đã được xác định từ trước, thường được gọi là xác suất tiên nghiệm. Các xác suất P(A_i│B) ,i = 1, 2, . . . , n được xác định sau khi đã có kết quả thí nghiệm nào đó thể hiện qua sự xuất hiện của H, thường gọi là xác suất hậu nghiệm. Như vậy, công thức Bayes cho phép đánh giá lại xác suất xảy ra các sự kiện Ai sau khi đã có them thông tin về B.

Thuật toán phân lớp Naive Bayes

Là thuật toán cơ bản của phương pháp Supervised Learning (Học có giám sát) Phân loại dựa trên định lý Bayes

o Bài toán phân loại:

• Một tập dữ liệu huấn luyện D_train, trong đó mỗi phần tử dữ liệu x được biểu diễn là một vectơ n chiều: (x_1,x_2,...,x_n)
• Một tập xác định các nhãn lớp: C={c_1,c_2,...,c_m}
• Với một phần tử z mới, thì z sẽ được phân vào lớp nào?

o Thực hiện phân loại cho z:

• Trong phương pháp phân loại Bayes, giả sử các thuộc tính là độc lập có điều kiện với các lớp nên ta có:
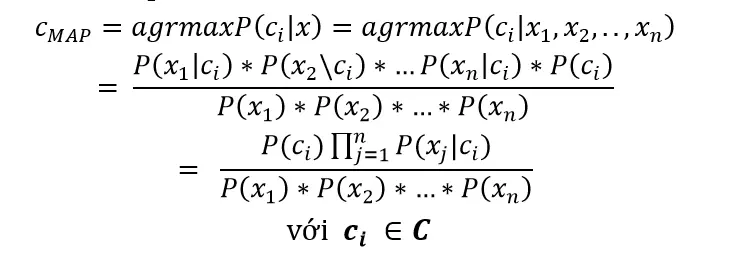
• Vì xác suất tiên nghiệm P(x_1 )P(x_2 )…*P(x_n )là như nhau nên ta suy ra:
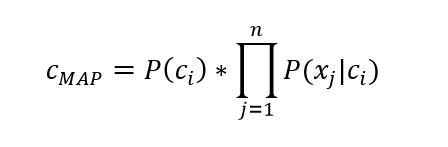
• Phân loại Naïve Bayes tìm phân lớp có thể nhất đối với z

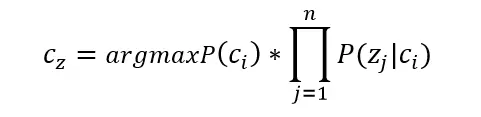
(to be continued)